金融衍生品定價模型及二階段運算

王 娟

（1.南京大學商學院，江蘇 南京210003；2.南京郵電大學 經濟與管理學院，江蘇 南京 210046）

0 引言

隨著利率市場化改革和金融創新進程的加劇，金融衍生品種類也日益增多，第一是尋找一種對所有衍生品定價工作都適用的定價方法至關重要，其次是定價行為在金融交易中頻繁發生，如德爾塔套利保值技術在華爾街每天被使用幾百次，那么具有強數學理論的定價方法具有操作難度，特別是對一般投資者非常不利，會造成有效需求不足，無形中阻礙了金融創新發展的步伐。基于此，筆者意圖將常見的三種衍生定價模型進行細致的公式分析，并對每一個變量和轉化過程進行淺顯易懂的闡述。同時針對目前定價公式的二階段運算進行推導，意圖提高中小投資者在進行衍生品交易過程中的定價能力和識別能力，以作出正確的決策。

1 衍生品定價的博弈論模型及二階段推導

在介紹模型之前，提出幾個假設：首先投資者不存在資本約束即初始投資是一個非約束量，這個量只取決于投資者意愿。其次是幾乎所有衍生定價法都強調過的無風險利率借貸。第一個假設其實在已有的各種模型推導中都已被包含，比如允許賣空（負債籌資以獲取股票，并且償還期限未定）。第二個假設非常必要，因為利率風險已經成為作為借貸主體的商業銀行等金融組織面臨的一個主要風險，如歐洲債券市場采用辛迪加循環技術——金融機構在貸款期限內有權調整利率水平，從而導致投資者面臨一定得利率風險，從而影響其決策。故假設衍生品協議日到到期日之間的利率穩定，這在目前是比較符合實際情況的。

1.1 二叉樹博弈

所謂博弈是指利益主體在既定利益前提下獲取最小風險的行為，在衍生品交易中交易商和投資者為了獲取利潤和降低風險會采取不同的定價策略、購買策略和執行策略。那么這種博弈的最終結果是無論作為標的物的股票價值如何變動，都會使其衍生品的價值即投資組合價值穩定——這是博弈定價法的本質。為了方便論述，下文均以股票歐式看漲期權為一種特殊的衍生品，歐式期權具有較強的約束性，投資者必須在到期日才能執行權力。

V-期權價值S——股票價值，X——購買期權數Y——購買股票數

那么在簽約日t0時刻，投資者作出決策，愿意花費單位的資本購買這兩種組合。C既是成本也是投資的即時價值，有表達式：

在到期日t1時刻，股票有漲有跌，正是這種不確定性導致了不同的投資價值未來值。用二叉樹分別表示這種股價和期權價值。（圖1）當股價從S0上升到Su，表示購買期權是很有價值的，很明顯U＞V0，相反股價下跌了，期權價值下跌到D。那么如何表示上漲和下跌時的投資價值呢？當股價上升時，投資者在到期日必然愿意執行期權，從期權市場以較低的約定價格購買期權，然后在股票市場上轉賣出去，以賺取差價。這時候投資引起的價值為：

相反，如果股價下跌，投資者必然不執行期權，因為繼續執行期權將會導致更多的損失。

這時：

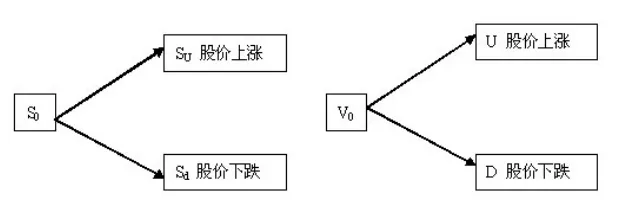
圖1 股票價值和期權價值的二叉樹模型

前面已經提到，定價的目的在于消除股價波動引起的風險引起的投資組合價值變動，即（2）式等于（3）式，可以求解得到股數Y和期權數X的關系。將（4）式子代入(1)式，并使 X=1，則，得到Ct1=V+D-U，初始資產Ct0=XV+YS0經過無風險利率r運行后，到1期后的價值為Ct1=(XV+YS0)er，經過換算得到，其中（4）式為仔細觀察期權價值的表達式，如果忽略分母因子，整個公式可以表述為期權價值等于賣空股票數量與股票價值現值的乘積，加上期權價格極差，經濟意義為：無風險利率水平與期權價值成反方向關系（因為D-U＜0），并且投資者群體對期權價格波動預期差異越大，期權價值越高，這也充分體現了利潤來自風險的基本定義。

對文、理科學生在9項技能的自我評價上進行獨立樣本T檢驗（見表2），結果顯示，除“翻譯”的P值=0.0 22＜0.05外，其他8項的P值均大于0.0 5，表明不同學科的學生對于絕大多數技能的自我評價沒有顯著性差異。而理科生在“翻譯”評價上的均值顯著地高于文科生，比起口語和寫作這種主動的創造性的輸出，理科生更喜歡用積累的詞匯機械地翻譯給予的文字段落，很好地說明了英語課堂上理科生更消極被動的一面。

1.2 模型改進及二階段運算

期權購買是一個連續的過程，不具有排他性，即一個投資者在某一時間購買，其他投資者也能在期權到期日之前的任何一天購買，哪怕在其他投資者之后。按照期權的預期差異性質，到期日越近，則預測結果更為準確和明朗，那么期權的價值下降。根據這一思路，將上文中t0和t1之間的時間段劃分為若干個更小的階段，可依次為t0,t11,t12,……t1k,…t1n-1,t1，其中,k=1,2…n。為了簡化分析，僅考慮二階段模型（圖2）。根據上文推導出的期權定價公式，筆者從圖2的第三期開始倒推，由3-1和3-2得到2-1點的期權價值為。

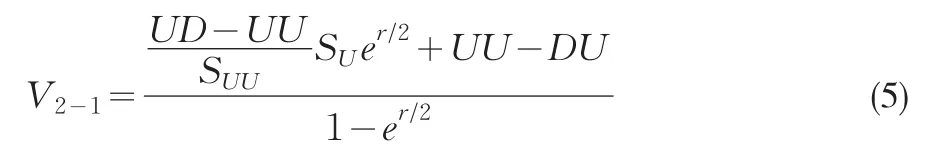
2-2點的期權價格：

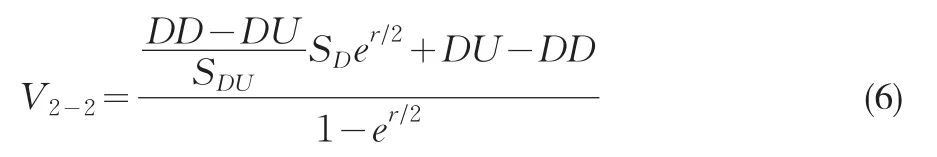
在上節分析中，在這兩點的U和D是已知的，屬于事后觀測，但這里（5）和（6）式分析的是評估值，故可以將U和D替換為V2-1和V2-2。得到最初期權價值（7式），可知無論將期限分為多少段，每一個節點代表的期權價值由其分出的兩個節點的期權價值（V2-2-V2-1）非常相關，可以這樣理解：股票價值振動幅度越大，期權價值越高；同時利率效應ert中的無風險利率水平越高，期權價值越大。

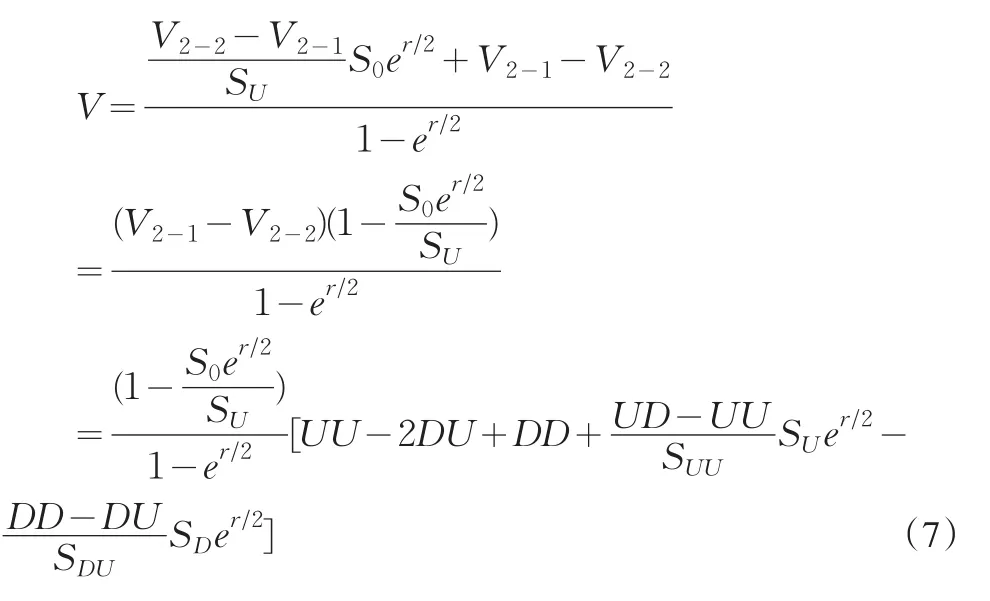
2 概率論法（期望價值法）

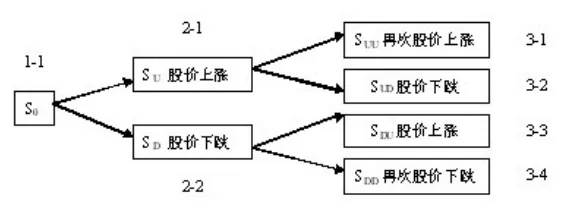
圖2 二階段二叉樹模型

2.1 預期與概率

博弈論法中將消除股價波動的價值影響效應降低到0，從某種程度上是實行一種概率，這種概率使得投資組合的預期組合收益與無風險利率引起的穩定收益相等，即沒有主體受損，假設初始時刻t0的股價為S0，人們均預期會有漲跌兩種狀況，當然有一定概率進行分布，上漲概率為P，下跌概率則1-P。期權的價格如同股票價格的靈魂一樣，始終不能與標的物價格分開。只要把這種升降概率找到，就可以對未來的期權價格預期進行運算，這種預期是否與上面的逆向運算結果一致，下面進行討論。

首先僅僅考慮股票收益預期，到期t1時刻的股票價值為：E(St1)=p(Su-St0)+(1-p)(SD-St0)，根據無套利定價愿意，S0投資在t1時刻的價值為St0er，兩者應該相等，計算出概率P=(St0er-SD+St0)/(SU-SD),若股價上漲和下降時對應的期權價格分別為U和M，執行價格為X，那么對應的期權價格應為U-X和D-X很明顯一正一負。則期權期望價值為：

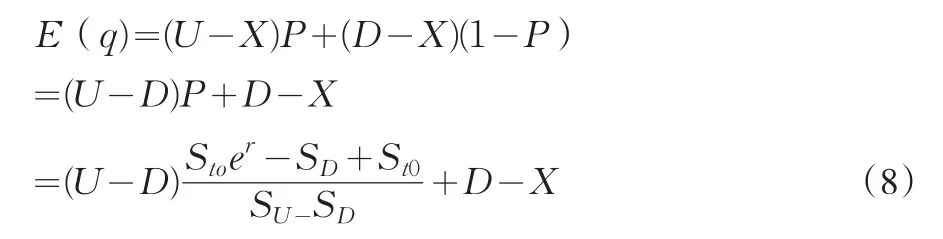
將E（q)除以er得到期權價格購買現值。針對推導出的模型具有以下解釋：

（8）式第二行表示期望期權價格的差價以一定概率發生，(U-D)P表示眾多投資者預期價格存在差異的前提下預期差異發生的概率期望值，D-X為股價一定下跌的情況下執行期權的損失值。可以理解為這樣一場賭博，看漲期權購買者純粹屬于看漲者，只有購買權而不能放棄購買權，到期日無論漲跌都必須按執行價購買該股票，結果只有兩種可能，當股價下跌時，必須損失D-X；但上漲時他不僅能夠獲得U-X的利潤，還可以將與他賭博的另一看跌投資者的D-X賭資給收回來，當然這一切都發生在概率為P的條件下。

2.2 二階段運算

同上節論述類似，筆者將目前到到期日之間期限分為2個時間段，分為四種情況：

第一種是股票在2期內持續上揚，到期后價值為SUU=U2S0，發生概率P2；

第二種是股票在1期內上揚，2期內下跌，到期后價值為SUD=UDS0，發生概率P(1-p)；

第三種是股票在1期內下跌，2期內上揚，到期后價值為SUD=DUS0，發生概率(1-p)p；

第四種是股票在2期內持續下跌，到期后價值為SUU=D2S0，發生概率P2；

以上U＞1,D＜1。則購買期望收益為：

可推廣到N段的情況E(N)=S0[UP+D(P-1)]n，其中UP+D(P-1)為漂移率，計算一只股票的長期漂移率對投資具有重大的指導意義。推導出概率為：

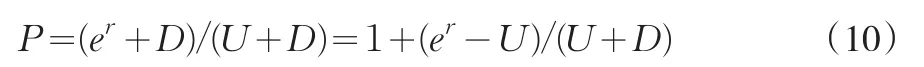
因為概率P小于1，所以U一定大于er，可將er視為向上漂移系數的最小下界趨近值。上漲時的期權價值為U2S0-X21,下跌時期權價值為D2S0-X21。得出期望圖2中2-1點的期權期望值為(U2S0-X21)P+(D2S0-X21)(1-p)，同理由3-3和3-4點得出2-2點的期權定價預期值為(D2S0-X22)P+(M2S0-X2)(1-p)，X21為股價首次為漲的二次期權定價，U和D為對應股價，X22為股價首次為跌的二次期權定價，D和M為對應股價。可以發現第二和第三種的期權到期后價值相等。那么可以計算出初始期權價值

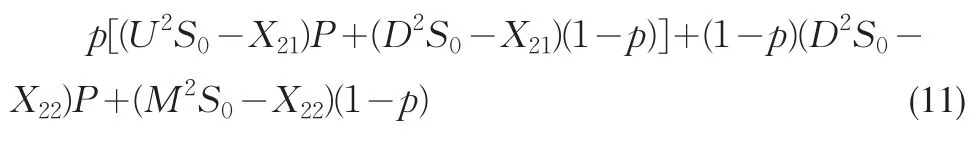
上式雖看似復雜，但也無非是加減乘除運算，針對于盈利為最終目的的期權投資行為來說，可以看作最為簡單實用的定價方法。這里要闡述一點：為什么將可以一階段處理的二叉樹模型區分為2階段？有效市場理論認為金融市場上任何信息均能從當期價格中反映出來，但在實際操作過程中這個理論假設并不成立，股票價格時間序列反映的信息仍然比當期單個數據包含的更多。這也是為什么在目前金融市場的實證研究過程中普遍采取高頻數據的原因。

3 資產組合復制技術

復制——一種建立不同投資組合，以不同組合到期日價值相等的定價方法，具有博弈等值和概率處理的內涵，可以視為上面兩種方法的綜合。假設不購買期權，只是進行正常的投資，常見的為股票和債券收益組合，為了方便計算，可以假設債券的價格為1，購買X單位股票和Y單位債券。資產組合價值可表示為：

一般來說，債券的利息是固定的，以無風險利率r獲取收益，經過1期之后的價值為er，同樣股票面臨漲跌兩種情況SU和SD。那么一期之后的資產組合價值為（13）式，可以復制一種期權使得漲跌情況下的期權價值與組合價值對應，故在式右邊加上相關等號。

如果僅X和Y未知，其他參數已知（這在現實中是成立的），可以由上面兩公式求出組合情況。

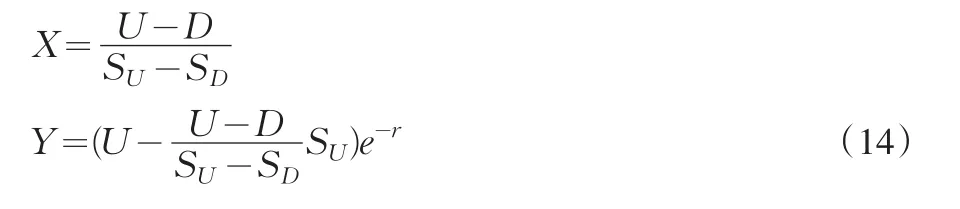
在第一節中，已經得到期權價值公式

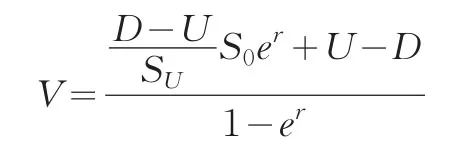
可以在推導過程中假設只購買一股期權和Y股股票，則可將此式子改為V=YS0+(u-YSu)e-r，將（14）式代入上式，可以得到：

V=e-r[qU+(1-q)d]其中

可以將q看作一種概率，是一定小于1大于0的一個數字，如果erS0＜SD，即q＜0，則表示即使股價下跌，購買期權也是穩賺的，這種情況基本不可能出現；erS0＜SU也是一定成立的，否則沒有投資者會冒著風險獲取小于等于無風險利率報酬。這里還是可以理解為一場賭博，以最差情況為基準，獲取最高利潤當然是最理想的狀況，但目前最有保障的是無風險利率收益，兩者比例可視為獲利概率。

4 總結

本文通過對三種金融衍生期權定價模型的推導，揭示了二叉樹模型下的定價規律，發現都具有概率路徑性質，目前代表性資產投資理論有均值——方差、資本資產定價、無風險套利定價等方法。這些模型之間互有聯系，或在假設上，或在結果上。同時又存在著不同的優缺點，基于二叉樹模型的三種套利定價方法也不例外，首先是假設股票有兩種情況——漲和跌，但在現實中不可能只有兩種定價，可能有無數種執行價格，那么簡單的二叉樹模型運用顯得很局限；并且很多投資者（尤其是實力雄厚的投資者）具有風險中性——預期收益和現實收益相同的情況下，哪怕前者有風險，對其來說也不會改變其投資決策，這就使得以套利為目的的定價方法失效。其次是求解困難，假設存在三種情況，股價漲、跌或不變，那么求解投資組合系數從線性代數角度是不可能的，因為三個方程和兩個變量無法相互迭代，Joseph(2004)為了解決這個難題，特構建類似于本文中資產組合復制技術的股票——債券組合模型，通過引入兩個初始利率和股票，得到三個未知數和三個聯立方程，但作出了非常苛刻的假設（這種假設實際當中并非成立）。最后，期權定價一般是事后操作，即以歷史數據的可觀測性為基礎，否則預測的期權最優價值U是不準確的，因為股市波動非常劇烈，規律性對一般投資者來說不明顯。筆者提出一個思路：如果擯棄有效市場假設理論，極力通過股價的歷史序列進行時間序列模型建模，探討出股價運行規律，在方程擬合優度非常良好的情況下，可以采用預測值為股票到期日最大價格，克服了事后觀測操作的缺陷，也避免了因不同漲跌情況帶來的預期值計算困難。

[1] （美）Joseph stampfli victor Goodman，蔡明超譯，金融數學[M].北京：機械工業出版社,2004.

[2] 吳恒煜,隨機挽回率馬爾可夫鏈模型下信用差價衍生品定價[J].系統工程,2006,(1).

[3] 鄭振龍,金融衍生品的定價能力研究:以中國市場權證為例[J].商業經濟與管理,2010,(2).