基于社會零售總額的非正常波動統計數據的季節調整

翁東東

（泉州師范學院，福建 泉州 362000）

0 引言

我國學者對非正常波動統計數據季節調整方法應用的系統研究相對較晚，目前實際操作是采取與上年同期的數據進行比較的方法來反映經濟的增長變化，如采用月同比的居民消費價格指數反映價格變動的一般趨勢，這種方法可以消除季節性因素的影響，但有它的局限性，即不能及時反映經濟變化的轉折點，并可能產生錯誤的結論[1]。研究表明，采用不經過數據季節調整（修勻）的數據與去年同期進行比較所反映的經濟周期的轉折點往往要平均滯后六個月。直到上世紀90年代，我國統計學理論界和政府統計系統的相關人士才開始接觸非正常統計數據季節調整（修勻）模型，但對其研究不夠深入。因此，研究由于季節、節假日或其他特殊原因導致的非正常波動統計數據季節調整方法，解決這些統計數據如何剔除非正常因素的問題，是我國迫切需要解決的一個重要課題[2]。這一研究不僅對準確計算相關統計數據有十分重要的理論意義，而且對我們統計實際工作過程中可操作性強的具體處理方法、歷史數據的可比性以及探索經濟變化的規律都有重要的現實意義。

目前，國內外學者對非正常波動統計數據季節調整的方法大致包括指數平滑法和X-12-ARIMA季節調整方法【3】。國內有些學者運用X-12-ARIMA季節調整方法對消費價格指數等時間序列數據進行數據修勻研究，如張鳴芳等（2004）以上海的月度數據為例，在考慮春節效應的情況下，使用TRAMO/SEATS程序對CPI進行了季節調整，但對調整后的數據沒有做進一步的分析【4】。欒惠德（2007）在明確界定CPI的性質及其處理方法的基礎上，對我國月度CPI數據進行了季節調整【5】。此外，張鳴芳（2005）也對中國季度GDP的季節調整作出簡要的分析，她認為中國GDP有顯著的季度間季節性變動特征,但不存在年度間的變動季節性特征，即顯現出非常有規律的季度季節性變動【6】。

1 非正常波動統計數據季節調整方法選擇與數據檢驗

本文采用的定量方法包括指數平滑法、單位根檢驗、協整檢驗、向量自回歸等方法，對數據季節調整方法研究以總量指標和相對指標為例予以研究，其中總量指標數據季節調整可歸為單變量時間序列季節調整，相對指標數據季節調整可歸為多變量時間序列修勻。本文總量指標以歷年我國社會消費品零售總額為例予以例證；相對指標以居民消費價格指數（環比和定基）與工業品出廠價格指數（環比與定基）為例予以實證。在實證中對建立的修勻模型得出的修勻值與實際情況進行比較，同時，在建模前首先對研究對象作單位根檢驗，隨后建立相應的向量自回歸（VAR）。

1.1 向量自回歸模型

向量自回歸(VAR)模型是基于數據的處理多個相關經濟指標關系的重要模型之一，并且在一定的條件下，多元MA和ARMA模型也可轉化成VAR模型。向量自回歸模型通常要求回歸中的變量是平穩的，如果變量是非平穩的，則可以考慮利用向量離差修正模型【7】。就本文所研究的CPI和PPI數據而言，符合上述模型的適用條件：（1）研究的CPI和PPI數據都屬于宏觀經濟數據；（2）選取的數據是2005年1月～2010年3月的CPI和PPI環比定基數據，樣本容量為63個，達到了應用VAR模型的要求；（3）由單位根檢驗結果可知環比的居民消費價格指數（CPI）與工業品出廠價格指數（PPI）都為平穩變量。

1.2 數據的平穩性檢驗分析

用ADF單位根檢驗方法來分析數據的平穩特征。各數據均為我國的相關經濟指標數據，其中定基指數將2004年12月的水平定義為100，包括：社會消費品零售總額、居民消費環比價格指數（以上月價格為100）、居民消費定基價格指數（2004年12月價格為100）、工業品出廠環比價格指數（以上月價格為100）和工業品出廠環比價格指數（2004年12月價格為100），數據均為2005年1月～2010年3月的月度數據。

經典計量回歸模型是建立在穩定數據變量基礎上的，對非穩定變量使用經典回歸模型，可能會出現虛假回歸問題。但是，如果變量之間有著長期的穩定關系，即它們之間是協整關系，可以使用經典回歸模型方法建立回歸模型。為此，本文對有關變量進行了ADF單位根檢驗和估計模型的協整檢驗。

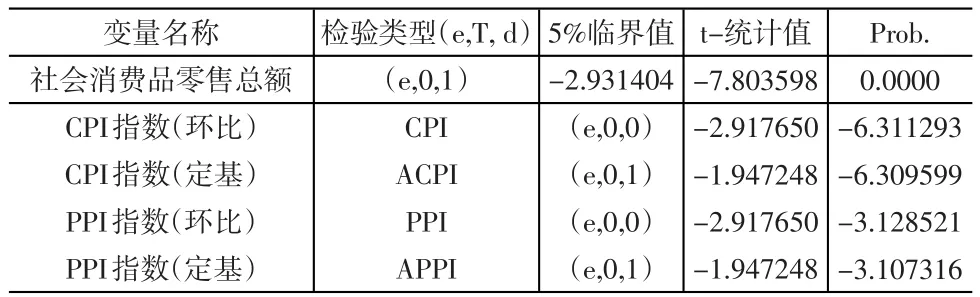
表2 有關變量的Augmented Dickey-Fuller(ADF)單位根檢驗

由表2的ADF單位根檢驗結果可知在5%的置信水平條件下，社會消費品零售總額、定期CPI（以2004年12月價格為100）和定期PPI（以2004年12月價格為100）需要差分一次后為平穩變量，因此他們都為I(1)。而環比CPI（以上月價格為100）、環比PPI（以上月價格為100）是平穩的，即I(0)。

2 非正常波動時間序列數據修勻方法實證分析

2.1 總量指標季節調整實證分析

在對上述指標進行平穩性檢驗后，筆者認為我國社會消費品零售總額具有直線趨勢，為一階單整，故社會消費品零售總額（e,0,1）用一階差分指數平滑法較為合適。在此基礎上，以2005年1月～2010年3月的社會我國消費品零售總額數據為例，具體數據見表3。從表3中的我國社會消費品零售總額數據來看，這一時期的時間序列數據總體趨勢明顯向上。因此，平滑系數α應當取大小適宜的數值，一般在0.3～0.5之間【8】。

從圖1所展現的時間序列變動趨勢來看，我國社會消費品零售總額總體呈現直線向上態勢。當時間序列的變動具有直線趨勢時，用一次指數平滑法會出現滯后偏差，其原因主要是給定的數據不能直接滿足一次指數模型的要求。我們可以運用一階差分先對給定的時間序列數據進行處理，使之能夠適合一次指數平滑模型要求，然后再對處理后的結果做返回處理。具體公式如下【9】。

表3 2005年1月～2010年3月我國社會消費品零售總額數據 （單位：萬元）

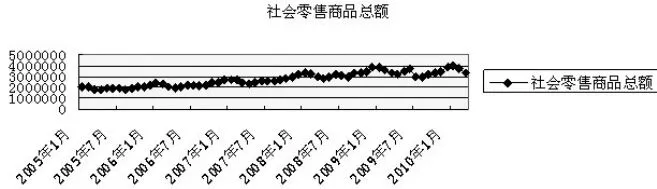
圖1 2005年1月～2010年3月我國社會消費品零售總額趨勢圖

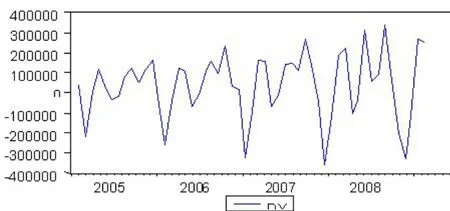
圖2 2005年1月～2010年3月我國社會消費品零售總額一階差分序列圖

一階差分公式：

因此，我們首先利用Eviews 5軟件對2005年1月～2010年3月我國社會消費品零售總額進行一階差分處理，結果如圖2所示。從圖2我們可以看出，處理后的時間序列平穩性較好，基本符合平穩時間序列的要求。然后我們再利用Eviews 5軟件對表3中的時間序列數據進行指數平滑處理，輸出結果表明：上述時間序列數據模型的平滑系數（即Alpha）為0.4900，殘差平方和為30.16720，預測離差的均方根為0.747430，均值為733557.8，趨勢項為30.37037。其中，該時間序列模型的平滑系數小于0.5，符合本文前面所提出的指數平滑系數選擇標準。那么，我們可以得出我國社會消費品零售總額指標的季節調整模型為：

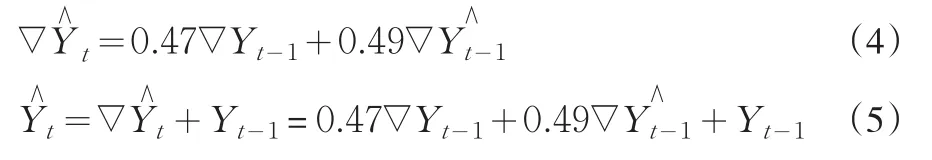
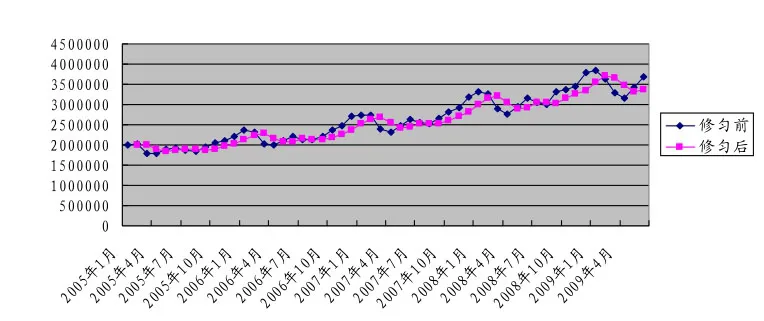
圖3 數據修勻前后的社會消費品零售總額趨勢對應圖（單位：萬元）

2.2 相對指標季節調整實證分析

向量自回歸模型通常要求回歸中的變量是平穩的，如果變量是非平穩的，則可以考慮利用向量離差調整模型。對于環比價格指數與定基價格指數通常會有不同的平穩特性，為了同時說明不同平穩數據的處理程序，考慮到CPI與PPI都是兩個相互關聯的重要經濟指標。因此，本文分別對環比和定基的CPI指數和PPI指數進行數據處理，并在所得結果基礎上給出VAR模型的適用環境的選擇建議。

2.2.1 相對平穩波動的數據季節調整方法實證分析

由前面的單位根檢驗知環比的居民消費價格指數（CPI）與工業品出廠價格指數（PPI）都為平穩變量，因此可以對其直接建立VAR模型，定義各變量在VAR模型中的先后順序依次為CPI、PPI，則yt=(CPIt，PPIt)T。

VAR模型中一個重要的問題就是滯后階數的確定。在選擇滯后階數p時，一方面想使滯后階數足夠大，以便能完整反映所構造模型的動態特征。另一方面，滯后階數越大，需要估計的參數也就越多，模型的自由度就越小。所以通常進行選擇時，需要綜合考慮，既要有足夠數目的滯后項，又要有足夠數目的自由度。通過觀察該組變量所構成的VAR模型的單位圓圖發現，當滯后結束大于等于10時，模型便不具有穩定性，綜合考慮極大似然值準則LR，選擇滯后階數為9。通過建立VAR(9)，得到模型結果，從而得知該VAR(9)模型(式（6）)特征多項式的逆根都在單位圓內，因此該VAR(9)模型是穩定的，可以用其做進一步分析。利用所建的VAR（9）模型可運算出初步調整的CPIt、PPIt序列，后文將對這兩列做進一步平滑處理。

2.2.2 季節調整的結果

在此，我們對經VAR（9）模型調整過的序列通過雙指數平滑法，做進一步調整。根據指數平滑法理論，結合數據趨勢特性，取調整后CPItPPIt的平滑系數為0.2，而調整后的ACPIt、APPI取平滑系數為0.4，可得到的平滑序列圖如圖5～圖8所示。圖5～圖8中的變量名加后綴-0SM的曲線為調整后的曲線，以圖5的環比CPI的調整對比圖為例，調整前的CPI曲線波動振幅較大；而調整后的曲線圖明顯平滑許多，且振幅大幅縮小。通過觀察其他季節調整后的序列曲線與原始序列曲線的對比圖，可見其調整后的曲線較平滑，調整效果比較合理。

以2008年2月為例，該月的環比CPI調整前的數值為102.9，利用所建的VAR（9）模型可運算出初步調整的CPI序列并進行平滑處理后，我們得出季節調整后的相應環比CPI數值為100.2，修勻前后離差為2.7%。這一離差主要是受我國傳統消費習慣影響，我國傳統節日春節大致在2月前后，在這一階段內群眾消費需求相對增加，導致該月CPI較上月環比大幅度上漲。為了更真實地反映這個月CPI數據的實際變動情況，運用VAR模型對其進行平滑處理，在一定程度上剔除了節假日因素影響，使之更加符合實際情況。

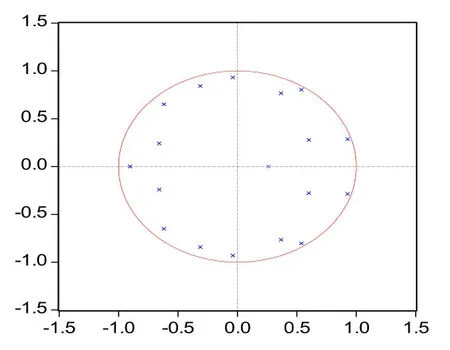
圖4 VAR(9)的AR根單位圓圖

3 結論與不足之處

根據總量指標的特性，本文采用指數平滑法對非正常波動的福建省社會消費品零售總額數據進行季節調整。其主要結論如下：

(1)季節調整模型

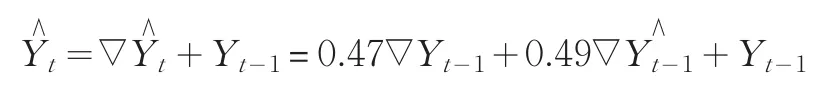
(2)該模型可剔除總量指標（我國社會消費品零售總額數據）非正常波動因素。在實際工作中將相關的時間序列數據代入這一季節調整模型，從而得出相應的時間序列季節調整值，這有助于我們更準確地剔除總量指標（我國社會消費品零售總額數據）非正常波動時間序列數據剔除非正常波動后的實際情況。

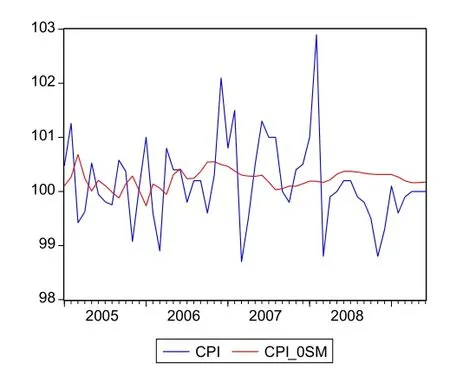
圖5 環比CPI數據修勻對比圖

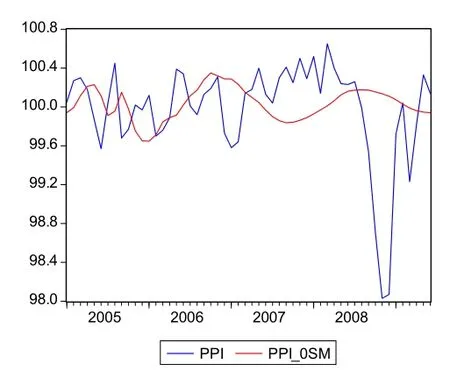
圖6 環比PPI修勻修勻對比圖

圖7 定基CPI數據調整對比圖

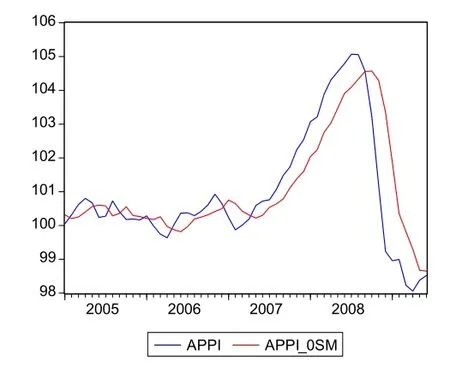
圖8 定基PPI數據調整對比圖

(3)可直接運用分析軟件剔除總量指標非正常波動因素。在目前統計系統常用的軟件馬克威分析系統或Excel中的均有“指數平滑”分析工具。

（4）可依此辦法建立其他總量指標剔除非正常波動因素的模型，也可以直接用建立的模型季節調整非正常波動的總量指標。

根據相對指標的特性，本文采用向量自回歸對非正常波動的相對指標（CPI和PPI數據）進行調整。其主要結論如下：

(1)調整模型見公式（4）和（5）。

(2)模型可剔除相對指標（CPI和PPI）的非正常波動因素。在實際工作中將相關的時間序列數據代入這一季節調整模型，從而得出相應的時間序列調整值，這有助于我們更準確地剔除相對指標（CPI和PPI）的非正常波動時間序列數據剔除非正常波動后的實際情況。

(3)可直接運用Eviews、SAS、SPSS等計量分析分析軟件剔除相對指標的非正常波動因素。通過上述指標時間序列圖季節調整前后的對比分析，調整后的曲線較平滑，可見其季節調整效果比較好，達到了預期的效果。

本文對非正常波動統計數據修勻方法進行的研究，還存在有待完善之處，主要有以下方面：

（1）現有計量分析軟件的不完全適合性。目前通用的經濟計量軟件多數是國外引進的，對季節和移動假日等因素調整時是針對西方的傳統因素（如復活節，圣誕節等）進行的，與我國的國情有所不同，比如我國的消費價格指數主要受到的春節、“五一”、“國慶”等假日的影響在模型中就無法剔除。因此，使用一般的計量分析軟件直接進行調整時，所得的結果往往不能令人完全滿意。

（2）模型的調整值與實際數據有所偏差。對指數平滑法來說，模型最終得出的季節調整預測值的大小跟平滑系數的大小密切相關，而平滑系數的大小與給定的時間序列數據波動程度及其上升或下降的趨勢有關。本文主要是利用Eviews計量分析軟件對時間序列數據進行平滑處理，數據的波動程度和升降趨勢都會對計算得出的平滑系數有影響。因此，個別時間點的數據異常數值可能會導致部分月份的季節調整值與實際數據有所偏差。

[1] Pagan,A.R.Three Econometric Methodologies:An update in L.T.Oxley,C.J.Roberts,D.A.R.George and S.T.Sayer(eds.)Surveys in Econometrics[M].Massa Chusetts:Basil Blackwell,2001.

[2] Markku,L.,H.LüTkepohl.Identifying Monetary Policy Shocks Via Changes in Volatility[J].Journal of Money,Credit and Banking,2008,40(6).

[3] 中國人民銀行調查統計司.時間序列X-12-ARIMA季節調整——原理與方法[M].北京：中國金融出版社，2006.

[4] 張鳴芳，項燕霞，齊東軍.居民消費價格指數季節調整實證研究[J].財政研究，2003，

[5] 欒惠德.季節調整中的春節模型[J].經濟學季刊，2007，6（2）.

[6] 張鳴芳.中國季度GDP季節調整分析[J].財經研究，2005，（7）.

[7] 高鐵梅.計量經濟分析方法與建模[M].北京：清華大學出版社，2009.

[8] 王長江.指數平滑法中平滑系數的選擇研究[J].中北大學學報（自然科學版），2006,(6).

[9] Lütkepohl,H.New Introduction to Multiple Time Series[J].Berlin:Springer Verlag,2005.