基于魯棒反饋線性化的船舶航向魯棒內模控制
蔡旭東,曲 豐,崔滋剛,李 昌
(海軍91388部隊92分隊,廣東 湛江 524022)
基于魯棒反饋線性化的船舶航向魯棒內模控制
蔡旭東,曲 豐,崔滋剛,李 昌
(海軍91388部隊92分隊,廣東 湛江 524022)
針對具有不確定項的船舶航向非線性數學模型,結合魯棒反饋線性化方法和魯棒內模控制算法設計出了船舶航向的魯棒內模控制器。該方法先將船舶航向非線性數學模型魯棒線性化,在補償型船舶航向魯棒控制律的基礎上,設計出內模控制算法。魯棒內模控制器中的反饋濾波器可以抑制參數攝動引起的實際輸出與模型輸出的誤差,并對相關參數進行在線校正。以某船為例,利用Matlab/Simulink工具箱進行仿真研究,結果表明所設計的魯棒控制器具有較好的控制性能,對風浪干擾也具有很強的魯棒性。
船舶航向控制;非線性系統;內模控制;魯棒線性化
0 引言
航向控制是控制理論應用較早且取得成果較好的一個領域。自20世紀60,70年代以來,隨著我國船舶航運事業的發展,船舶航向控制系統的控制與設計呈現出很大需求,發展也非常迅速,各種新的控制算法逐漸替代了傳統PID控制。船舶在大洋航行時受到各種環境干擾和航行工況影響,船舶運動表現出非線性、不確定性、大滯后等復雜的動態特性,船舶運動的控制也表現為復雜的控制問題[1-2]。為了提高控制精度,針對船舶航向的非線性不確定性模型,研究魯棒性強的船舶航向控制器設計方法是目前船舶運動控制領域的一個研究熱點。
作為魯棒控制之一的內模控制,能同時兼顧系統的魯棒穩定性和控制性能,且只需對一個參數進行調整,整定方便、在線設計比較容易,且對純滯后有補償作用,一直受到工程界的重視[3-4]。本文針對具有不確定項的船舶航向非線性數學模型,根據不確定項與狀態輸入的匹配型條件,對其進行線性化處理,并采用補償型魯棒控制律來設計船舶航向控制律。通過魯棒內模控制器中的反饋濾波器,抑制參數攝動引起的實際輸出與模型輸出的誤差,并對相關參數進行在線校正。以某船為例進行仿真研究,結果表明所設計的魯棒控制器具有較好的控制性能,對風浪干擾也具有很強的魯棒性。
1 系統描述
在船舶運動中,由于航行中船速、裝載狀態等都是變化的,同時還受風流浪等外界干擾的作用,會引起參數的攝動,因此控制系統設計中模型可采用下列具有不確定性項的Nomoto模型:
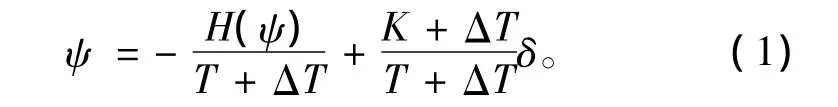
式中:H(ψ)=α0+α1ψ+α2ψ2+α3ψ3;αi(i=0,1,2,3)為Norrbin系數;K,T為操縱性指數。由裝載變化和風力等引起的ΔT,ΔK為參數不確定性項,其估算較為復雜,本文考慮航速變化ΔV引起的參數攝動,令
取狀態變量x1=ψ,x2=ψ=r,u=δ為輸入舵角,y=x1為輸出。船舶航向非線性系統的關系度等于系統的階數,是單輸入單輸出仿射非線性系統,則船舶航向非線性模型可表示如下仿射型不確定非線性系統形式:
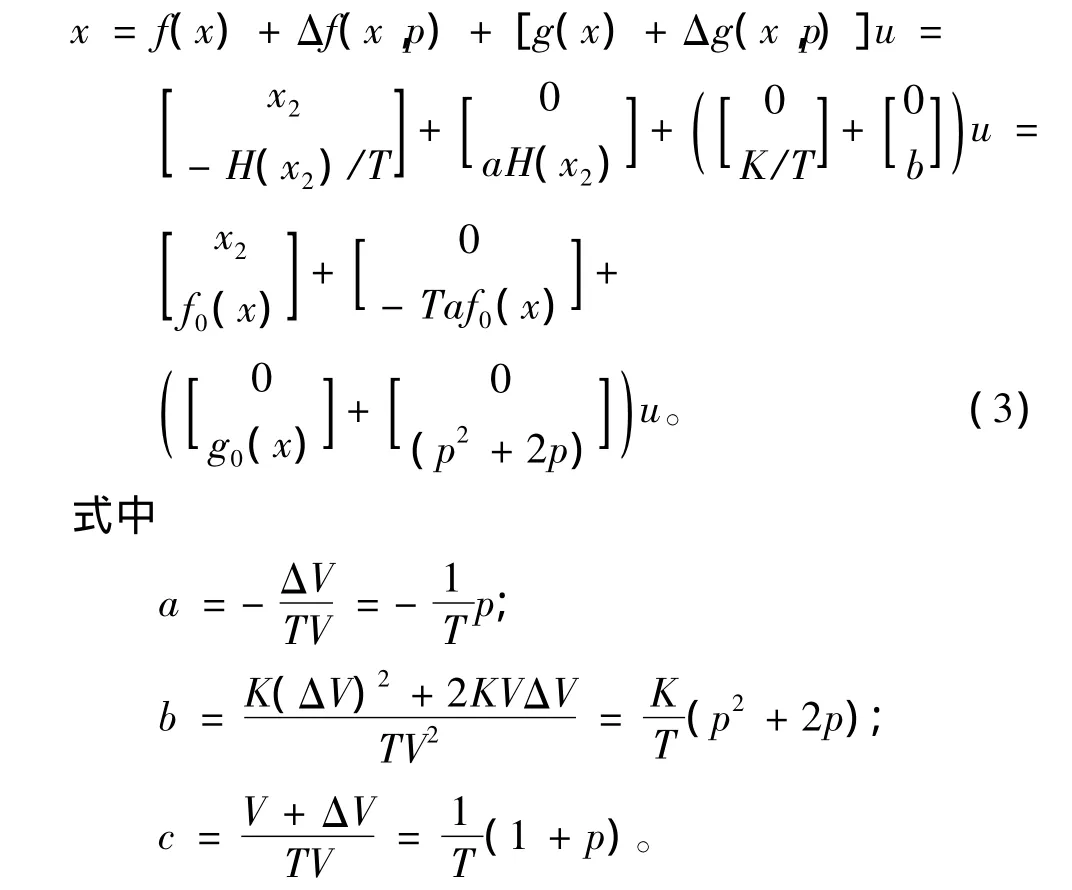
又根據匹配型條件式有:
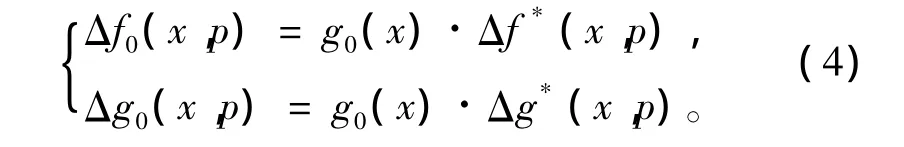
其中分離項有:
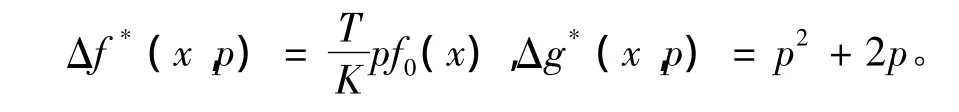
上述船舶模型為匹配型模型。當 Δf(x,p)=Δg(x,p)=0時,有α0=α2=0;該船舶航向非線性系統模型為標稱模型。
2 魯棒控制器設計
本文針對具有不確定項的船舶航向非線性數學模型,根據不確定項與狀態輸入之間的匹配型條件,對其進行線性化處理,并采用補償型魯棒控制律來設計船舶航向控制律。通過魯棒內模控制器中的反饋濾波器,抑制參數攝動引起的實際輸出與模型輸出的誤差,并對相關參數進行在線校正。
2.1 魯棒線性化[5-6]
根據式(3)的標稱系統,各階李導數有:
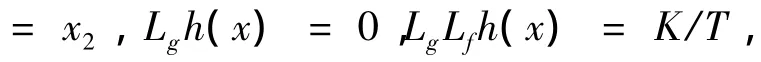
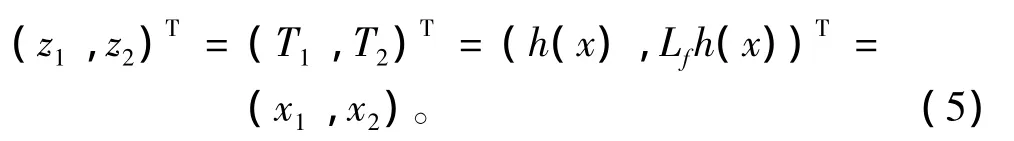
結合式(4),可以推導出:
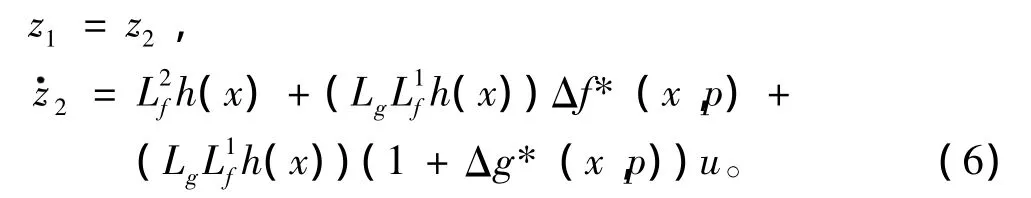
采用補償型控制律:
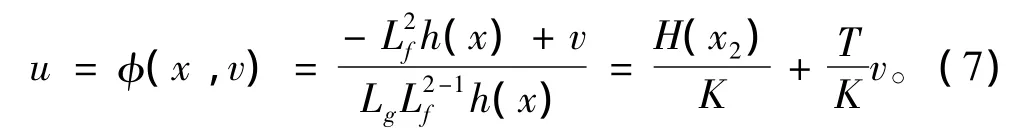
2.2 魯棒控制律設計
首先取外部控制輸入為外部輸入vd、極點配置K—z和補償器vs之和,即:
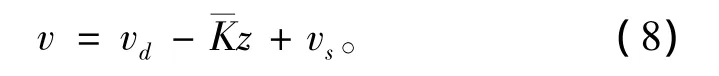
式中:為極點配置的正常數列向量;vs為1個反饋型補償器;q=[q1,q2]為在線調節參數,是標量常數,具有如下形式:
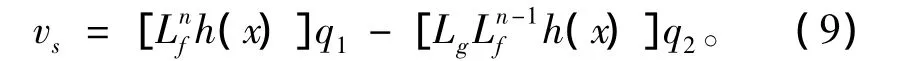
式(9)的表示形式并不惟一,這里它用只帶有2個調節參數的簡單結構來補償控制系統的不確定項。結合式(6)~式(8),可以得到:
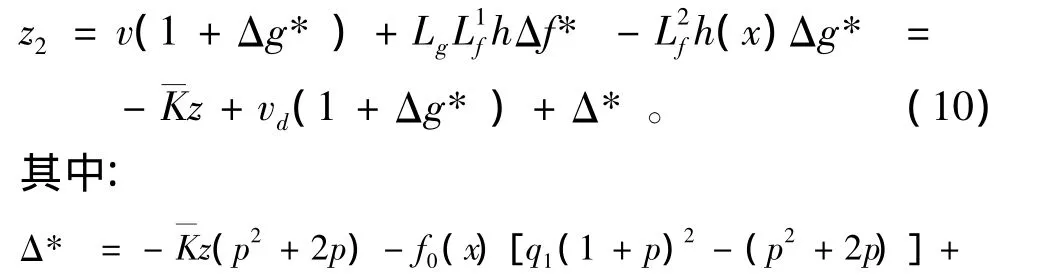

進一步轉換為可控制形式:
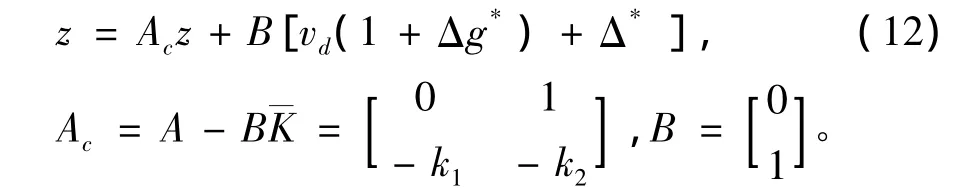
2.3 穩定性分析
下面將利用Lyapunov函數法分析上述船舶航向非線性魯棒控制系統的穩定性。
取Lyapunov函數法為:V=zTPz。其中P為實對稱正定矩陣。沿著式(12)所示函數的軌跡求微商可得到:
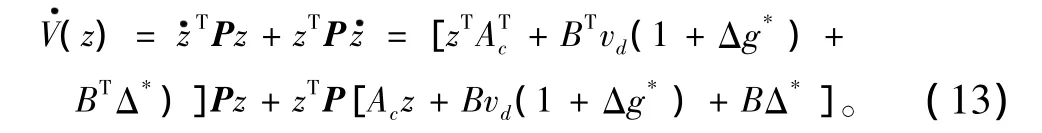
考慮式(12)中(Ac,B)為完全能控型,則有對稱正定矩陣Q,使得:
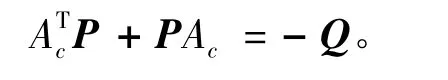
代入式(13)得:
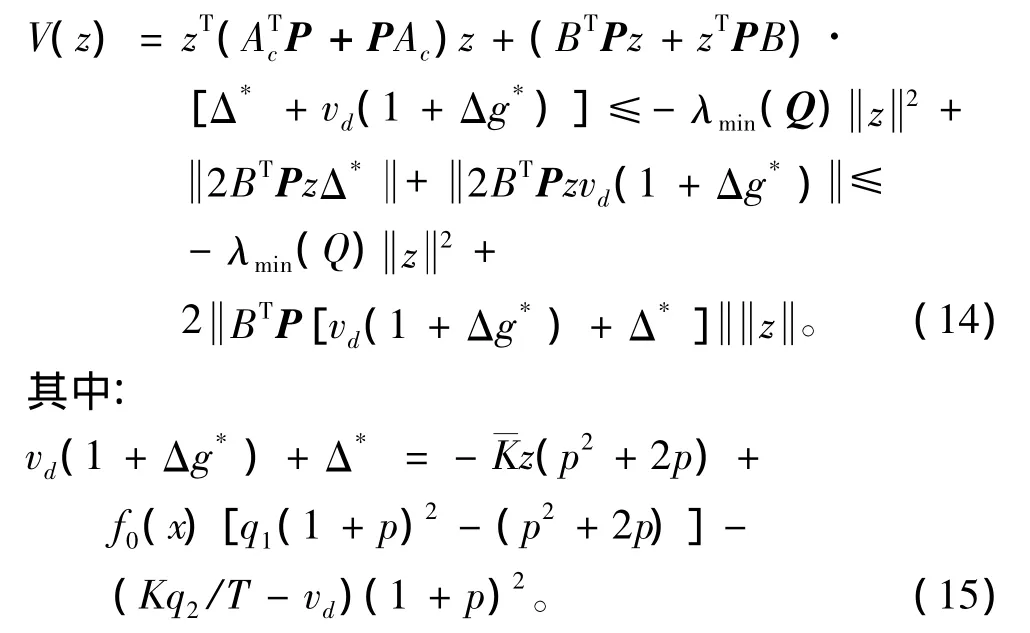
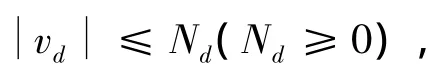
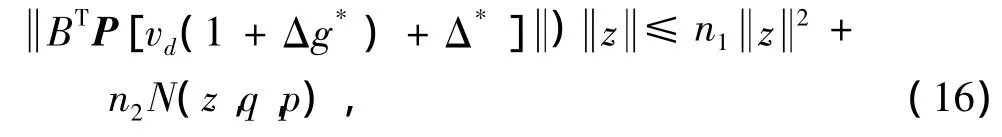
則式(15)化為:
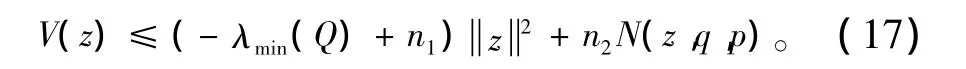
因此,適當地選擇矩陣Q和參數q=[q1,q2],可以使得V(z)≤0。經過上面的推導分析可知,通過適當選擇參數來設計補償器vs(x,q)的方法,大致抵消掉閉環系統的不確定項,但選擇參數[q1,q2]有很大的靈活性。內模控制是魯棒控制器設計的一種新型控制方法,具有良好的跟蹤性能和抗外擾能力[7-8]。下面在補償器vs的基礎上,引入魯棒內模控制(IMC)的方法來在線整定回路參數,在濾波器的作用下抑制系統輸出誤差y-ym的影響,增強系統的魯棒穩定性,保證系統輸出有效地跟蹤期望輸出。
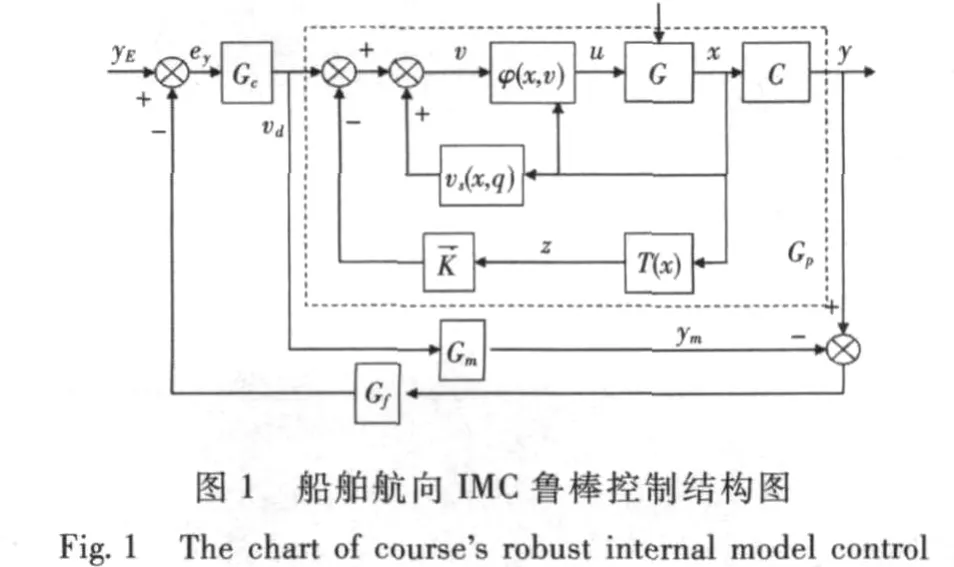
圖1中,ym為內模模型輸出,Gc為內模控制器,Gf=1/(λs+1)2為反饋濾波器,Gm為內模模型:
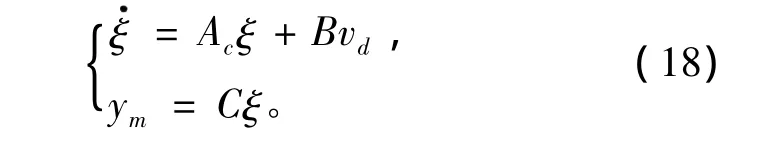
內模控制器
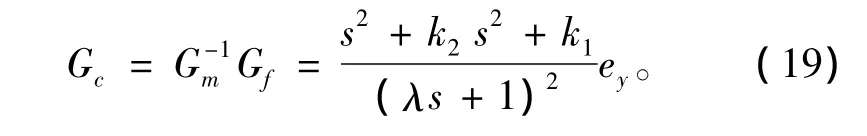
基于內部模型和反饋濾波器設計的內模控制律為
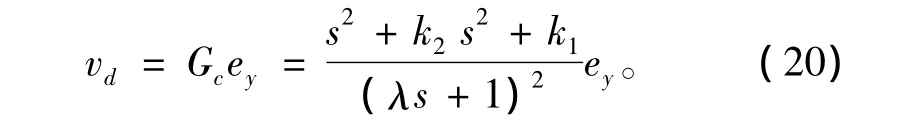
式中:ey=yE-(y-ym)Gf,yE為期望輸出;λ為濾波器常數參數。
3 仿真
以某船為例進行仿真實驗研究[2],仿真參數有:船長L=126 m,船寬B=20.8 m,滿載吃水d=8.0 m,方形系數Cb=0.681,航速V=7.7 m/s,T'=12.77,K'=8.12。通過計算可得K=K'V/L=0.4963,T=T'L/V=208.91,Norrbin 系數 α1=1,α3=30,KE=1。各設計參數相應取:K—=[0.07,0.001]T,改變航向角 ψ=+20°。
取濾波器系數λ=6,在標稱模型下,q取不同值時得出的航向和舵角的輸出曲線見圖2和圖3所示。
取q=[1,10]時,在標稱模型下,λ取不同值時得出的航向和舵角輸出曲線見圖4和圖5所示。
只考慮參數攝動時,不同參數攝動下航向角的輸出曲線見圖6所示。當同時取攝動p=-1/3,λ=1,q=[1,10],將風、浪等干擾的影響等效成正弦和隨機信號加入到舵角輸入進行仿真,得到的航向輸出曲線見圖7和圖8所示。
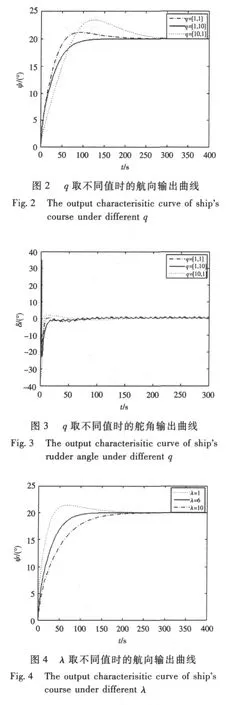
根據仿真結果圖2和圖3,可以分析出在濾波器系數λ不變的情況下,補償器vs(x,q)的參數q=[q1,q2]的選取可以影響到船舶航向控制系統輸出的超調量和調節時間。隨著q1的增大,航向角和舵角的超調量由無到有,并逐漸增大,調節時間也越長。而隨著q2的增大,航向角和舵角的超調量逐漸減小,且調節時間越短。從圖4和圖5可以看出,在補償器參數不變的情況下,濾波器系數的選取也同樣影響到船舶航向控制系統輸出的超調量和調節時間。隨著λ的增大,航向角和舵角的超調量逐漸減小,但調節時間更長。從仿真圖6~8可以看出,外界干擾信號對船舶航向影響較小,舵角和首搖角速度的輸出較穩定,出現的超調也在航向自動舵的控制性能指標以內。仿真實驗表明,采用基于魯棒線性化的魯棒內模控制算法可以有效地跟蹤、保持船舶航向,對外界干擾和模型攝動具有較強的魯棒性。
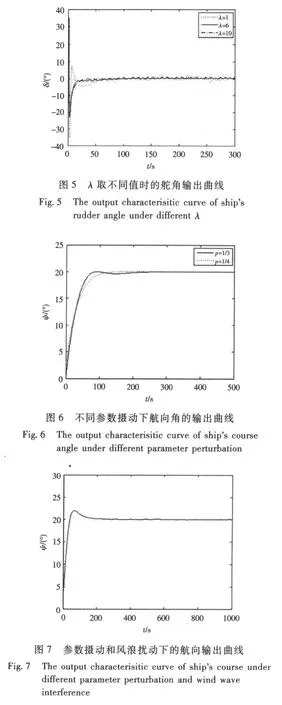
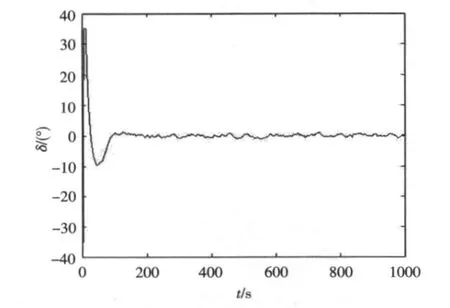
圖8 參數攝動和風浪擾動下的舵角輸出曲線Fig.8 The output characterisitic curve of ship's rudder angle under different parameter perturbation and wind wave interference
[1]DO K D,JIANG Z P,PAN J.Robust global stabilization of under actuated ships on a linear course:state and output feedback[J].Int.J Control,2003,76(1):1 -17.
[2]孔令濤,杜佳璐,王玉杰.基于逆推非線性阻尼算法的船舶航向控制器設計[J].大連海事大學學報,2006,32(4):61-64.
KONG Ling-tao,DU Jia-lu,WANG Yu-jie.Ship steering controller design based on backstepping algorithm and nonlinear damping algorithm[J].Journal of Dalian Maritime University,2006,32(4):61 -64.
[3]周涌,陳慶偉,胡維禮.內模控制研究的新發展[J].控制理論與應用,2004,21(3):475 -482.
ZHOU Yong, CHEN Qing-wei, HU Wei-li. New developments of research on internal model control[J].Control Theory & Applications,2004,21(3):475 -482.
[4]趙曜.內模控制發展綜述[J].信息與控制,2000,29(6):526-531.
ZHAO Yao.A survey of development of internal model control[J].Information and Control,2000,29(6):526 - 531.
[5]CHOU Yi-Shyong,WU Wei.Robust controller design for uncertain nonlinear systems via feedback linearization[J].Chemical Engineering Science,1995,50(9):1429 -1439.
[6]SASTRY S.Nonlinear systems[M].北京:世界圖書出版公司北京公司,2007.417 -422.
[7]潘立登.先進控制與在線優化技術及其應用[M].北京:機械工業出版社,2009.123 -134.
[8]HU Q,SAHA P,RANGAIAH G P.Internal model control with feedback compensati-on for uncertain nonlinear systems[J].Int J Control,2001,74(14):1456-1466.
Robust internal mode control for ship autopilot based on robust feedback linearization
CAI Xu-dong,QU Feng,CUI Zi-gang,LI Chang(92 Unit of 91388 Naval,Zhanjiang 524022,China)
In allusion to the nonlinear uncertain ship model,a robust internal mode controller for ship autopilot was put forward by using robust feedback linearization technique and robust internal mode control algorithm.The feedback filter in robust internal mode control was employed to dispel the error caused by parameter perturbation between model output and anticipant output,where the parameters were on-line tuned.The simulation results based on the Matlab/Simulink package showed that the effectiveness of the designed controller.It can track the desired course accurately and exhibit strong robustness peculiarity to the uncertainties of nonlinear ship model.
ship autopilot control;nonlinear system;internal model control;robust linearization
TP273;U664
A
1672-7649(2011)12-0037-05
10.3404/j.issn.1672-7649.2011.12.008
2011-01-04;
2011-03-04
蔡旭東(1985-),男,碩士,助理工程師,主要研究領域為信號探測處理與系統控制、系統試驗航路航向設計與優化等。

