多容慣性標準傳遞函數的建立與比較

楊 平，余 潔，孫宇貞

(上海電力學院電力與自動化工程學院，上海 200090)

在控制器的設計方法中，除了常規的頻域法、根軌跡法和狀態反饋極點配置法以外，還有一種標準函數設計法［1］.運用該設計方法時，一旦選定具有最優性能的標準傳遞函數，并推導出含有已知的受控過程模型參數和待求的控制器參數的閉環系統傳遞函數，則控制器參數就可通過簡單的代數運算算出，既不需要復雜的最優化算法，也不需要大量的整定試驗.正是由于這種方法的獨特思路和設計的簡捷性，近30年來吸引了不少學者對其進行擴展研究，并且取得了大量成果［2-10］.在應用標準函數設計法時，常用的閉環系統標準傳遞函數主要有兩種:ITAE標準傳遞函數［11］和Butterworth標準傳遞函數［12］.我國的學者在應用這兩種標準傳遞函數中發現了一些不足，并對其進行了一些完善，包括對ITAE標準傳遞函數的改進研究［13-16］和對 Butterworth標準傳遞函數的改進研究［17］.在形式上，所改變的是標準函數的多個系數數值.在實質上的改變有:積分時間域的縮短，重新優化計算，優化方法選用遺傳算法，其中最主要的是減少了超調量.在應用標準傳遞函數法設計控制器的過程中，筆者發現，除了上述兩種標準傳遞函數外，更好用的標準傳遞函數是多容慣性標準傳遞函數.

1 常用的閉環系統標準傳遞函數

1.1 ITAE標準傳遞函數

ITAE標準傳遞函數是使系統ITAE指標最小的閉環系統傳遞函數.根據文獻［13］，1型系統的ITAE標準傳遞函數為:

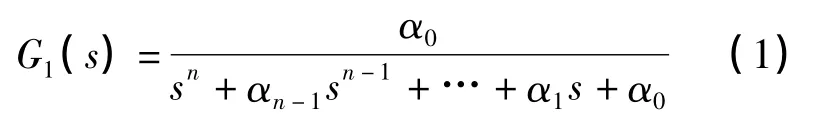
其1至8階函數的各系數值見表1.

2型系統的ITAE標準傳遞函數為:

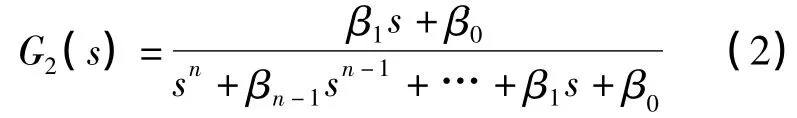
其2至6階函數的各系數值見表2.

表1 1型系統的ITAE標準傳遞函數1至8階的系數值

表2 2型系統的ITAE標準傳遞函數2至6階的系數值

在應用這些標準傳遞函數之前，先要設定閉環系統的自然振蕩頻率ωn，這個參數決定了閉環系統的快速性能(即閉環系統頻率特性帶寬).確定ωn時，既要追求快速理想性能，又要顧及實際的物理約束，因此需要經過數次的試湊.

1.2 Butterworth標準傳遞函數

Butterworth標準傳遞函數是通過將系統極點均勻地配置在根平面中以原點為中心、以ωn為半徑的左半平面圓周上形成的.根據文獻［1］，1型系統的Butterworth標準傳遞函數也如式(1)所示，但其1至6階函數的各系數值如表3所示.

表3 1型系統的Butterworth標準傳遞函數1至6階的系數值

同樣，在應用這種標準傳遞函數之前，先要設定閉環系統的自然振蕩頻率ωn.

2 多容慣性標準傳遞函數

2.1 多容慣性標準傳遞函數的建立

多容慣性標準傳遞函數為:

式中:T——慣性單元的慣性時間;

γi——多項式展開函數的系數，i=0，1，2，…，n－1.

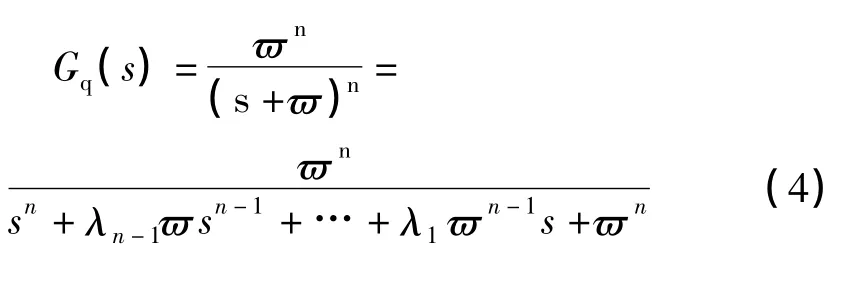
式中的系數λi(i=1，2，…，n－1)可根據代數學中的二項式定理推算得到，如表4所示.

由表4可以看出，多容慣性標準傳遞函數的系數值就是著名的楊輝三角形數陣中不含1的內核部分，推算過程非常簡單.例如，n=4時的系數值6可由n=3時的系數3+3得出，n=5時的系數值10可由n=4時的系數4+6得出，以此類推.

表4 多容慣性標準傳遞函數中的系數λi

當系數 λi(i=1，2，…，n－1)由表4得出后，則系數 γi(i=1，2，…，n －1)可由式(5)求得.

2.2 多容慣性標準傳遞函數的優勢

與ITAE標準傳遞函數和Butterworth標準傳遞函數相比，多容慣性標準傳遞函數有3點優勢:建立容易、無超調量和更便于工程應用.

通過多容慣性標準傳遞函數系數的建立過程，表明該函數的建立遠比其他兩種標準傳遞函數簡單，而且可以輕松地推算出任意高階的標準傳遞函數.

多容慣性標準傳遞函數所定制的系統只有負實數特征根，自然能實現零超調.而為了將ITAE標準傳遞函數的超調量壓低至5%以下，許多科研人員進行了大量研究.Butterworth標準傳遞函數的建立雖比ITAE標準傳遞函數要容易，但它所定制的系統的超調量遠大于ITAE標準傳遞函數，這也是Butterworth標準傳遞函數在工程中應用較少的原因之一.

應用ITAE標準傳遞函數和Butterworth標準傳遞函數時，必須先確定系統的自然振蕩頻率ωn.而應用多容慣性標準傳遞函數時，必須先確定慣性單元的慣性時間T.

在理論上，T和ωn只是互為倒數的參數，并無本質差別.但在工程應用上，慣性時間T的物理意義更直觀，更容易讓工程技術人員掌握.假如，一階慣性環節的過渡過程時間ts為慣性時間T的3倍，即ts=3T;n階慣性環節的過渡過程時間ts將為ts=3nT;那么，只要確定了期望的控制系統調整時間ts，就可輕松算得慣性單元的慣性時間 T，即 T=ts/3n.

假設 ωn=T=1，n=6，通過圖 1所示的Simulink試驗系統(選擇標幺系統，輸出量無量綱)進行階躍響應試驗，可得到圖2所示的結果.

圖1 Simulink試驗系統

圖2 4種標準傳遞的階躍響應曲線

由圖2可知，當多容慣性標準傳遞函數的慣性時間T=1時，ITAE標準傳遞函數的階躍響應最好，而多容慣性標準傳遞函數的響應最差.但若將多容慣性標準傳遞函數的慣性時間改為T=0.5，則多容慣性標準傳遞函數的響應就成為最好的.由此可見，通過慣性時間T的選擇，可以得到期望的理想響應.當然，這個理想響應能否實現，還取決于實際的物理約束條件.

3 結論

(1)在多容慣性標準傳遞函數的建立過程中，利用了代數二項式定理和楊輝三角形數陣，因此該函數具有了建立簡便、易于推廣到高階系統的特點.

(2)多容慣性標準傳遞函數所固有的無超調性能使其在動態特性上遠比ITAE標準傳遞函數和Butterworth標準傳遞函數優越.

(3)應用多容慣性標準傳遞函數所需整定的是慣性單元的慣性時間T，它比ITAE標準傳遞函數和Butterworth標準傳遞函數所用的自然振蕩頻率ωn更易被工程師掌握和應用.

［1］楊平，翁思義，郭平.自動控制原理:理論篇［M］.北京:中國電力出版社，2009:147-151.

［2］項國波.線性定常負反饋控制系統中的ITAE最佳調節［J］.中國科學:A，1980(2):185-192.

［3］雷迅.可控硅直流傳動控制系統中的ITAE最佳調節律［J］.自動化學報，1983(7):177-185.

［4］項國波.ITAE最佳控制［M］.北京:機械工業出版社，1986:1-230.

［5］陳明俊.ITAE最優Ⅲ型數字伺服系統［J］.自動化學報，1993，19(2):172-182.

［6］項國波，楊益群，楊啟文.一類單容純時滯系統二次優化控制［J］.信息與控制，1995，24(4):209-214.

［7］王永初.Butterworth濾波器在過程控制中的應用(Ⅱ)［J］.工業儀表與自動化裝置，1995(1):10-14.

［8］陳莊金.改進型高魯棒性校正器的研究［J］.儀器儀表學報，1999，20(3):254-256.

［9］田保峽，蘇宏業，褚健.基于狀態估計的PID控制器整定方法研究［J］.儀器儀表學報，2000，21(5):477-480.

［10］王偉，鄭耀林.一種采用Butterworth濾波器原理設計的具有高魯棒性的狀態反饋系統［J］.電子測量與儀器學報，2001，15(4):16-20.

［11］GRAHAM D，LATHROP R C.The synthesis of optimum transient response criteria and standard forms［J］.AIEE Trans，1953(2):273-275.

［12］SCHUKTZ W C，RIDEOUT C V.Control system performance measures:past，present and future［J］.IRE Trans Automatic Control，1961，26(2):270-275.

［13］李鎮銘.環路法及最佳狀態反饋系統設計［M］.北京:國防工業出版社，1988:1-200.

［14］楊益群，項國波.新的ITAE最佳傳遞函數標準型［J］.信息與控制，1999，26(4):259-265.

［15］張志涌，劉瑞楨.對經典ITAE傳遞函數標準型的研究［J］.福州大學學報，1977，25(3):120-121.

［16］李鐘慎，位移無靜差最優傳遞函數的研究［J］.自動化博覽，2007(2):82-84.

［17］洪健，李鐘慎.改進的Butterworth最佳傳遞函數標準型［J］.計算技術與自動化，2005，24(2):13-15.