層次分析法在土料場選擇中的應用

康迎賓，康 鵬，張戰強，宋勁草

（1.華北水利水電學院，河南鄭州 450011；2.洛陽市水利工程局，河南洛陽 471000）

土石料是水庫除險加固工程的主要建筑材料，而料場的合理規劃和使用是土石壩施工中的關鍵技術之一，是縮短工程建設工期、降低建設費用、保證施工質量的關鍵因素，而料場位置的選擇直接關系到施工總體布置格局。因此，在進入可行性研究和招標設計階段后，對料場選擇應持特別重視的態度，進行了多方面研究。

1 工程概況

洛陽市龍脖水庫位于洛河支流連昌河中游，坐落在河南省陜縣李村鄉龍脖村，水庫控制流域面積211 km2，設計灌溉面積0.43萬ha。工程1959年冬天開工建設，1973年建成，前后歷時15 a，形成現在規模，是一座具有灌溉、防洪、養殖等綜合效益的中型水庫。水庫建設于上世紀50年代，屬于“三邊”工程，工程運用至今，設備陳舊老化，建筑物多處存在工程隱患，水庫帶病運行，運行中發現許多問題亟待解決，安全鑒定其為三類壩。

在龍脖水庫除險加固工程中，所需天然建筑材料有土料、砂石料、塊石料三種，其中土料需求量為1.5萬m3。庫區周邊分布著眾多土料場，因此需要對其進行優化選擇，以滿足工程的需要。

考慮加固施工過程中料場對于工程建設的重要性，保證工程費用最低，兼顧施工環境、水土保持以及生態環境等要求，基于這幾方面的考慮既有常規的經濟、技術等定量性指標，也有環境保護等定性指標，對于定量指標與定性指標相結合的問題，常規的優化方法難于處理，故采用層次分析法。

2 層次分析法

人們在對社會、經濟等領域問題進行系統分析時，面臨的常常是一個由相互關聯又彼此制約的眾多因素構成的復雜而又缺少定量數據的系統。在做評價決策的時候，許多要考慮因素的優先程度往往難以量化，人的主觀選擇會起著相當重要的作用，這就給用一般的數學方法解決問題帶來了本質上的困難［1］。

層次分析法（Analytic Hierarchy Process，簡稱AHP）的提出為解決這類較為復雜的問題提供了簡潔而實用的方法。它是美國運籌學家T.L.Saaty教授于上世紀70年代初期提出的一種多準則決策方法。它在處理復雜的決策問題時，將問題層次化，分解為不同的層次結構，從而對方案層各要素進行優劣等級排序，最終選擇最優方案，為決策者提供了可靠的理論依據。

運用層次分析法建模，大體上可按下面四個步驟進行[2-5]：

（1）建立層次結構模型。首先將深入分析的實際問題層次化，將復雜問題分解為多個元素的組成部分，按其屬性及關系分解為不同的層次結構，構造出一個有層次的結構模型。上一層次的各要素對與其相鄰的下一層次各從屬要素起支配作用。

最高層：這一層中只有一個元素，稱為目標層。

中間層：由若干個層次組成，包含了為實現目標所要考慮的各種準則，又稱為準則層。

最底層：這一層包括可供選擇的各種決策方案，稱為方案層。

（2）構造出各層次中所有的比較矩陣。將層次結構模型的準則層、方案層中各要素對于其從屬于的上一層要素，構造成比較矩陣。例如：

式中：aij表示元素i和元素j相對于上一層某一元素進行比較時，i比j的相對重要程度，采用1～9的比例尺度法。其比例尺度及含義如表1所示。

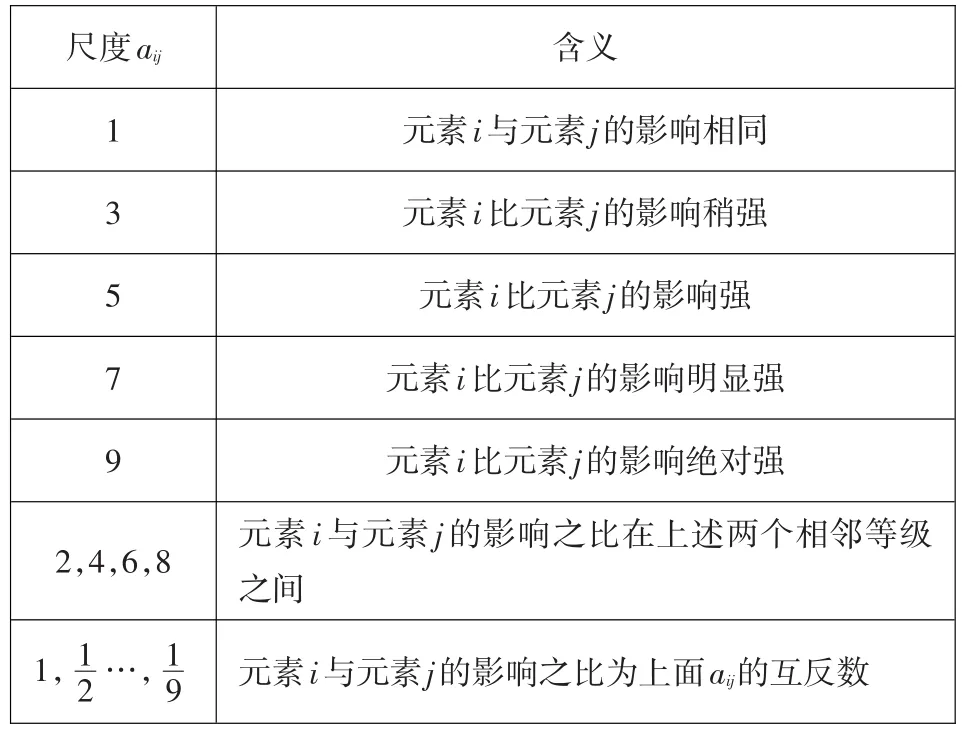
表1 判斷矩陣的比例尺度及其含義Table 1:Ratio and its meaning in the judgment matrix

（3）計算權向量并做一致性檢驗。計算每一個比較矩陣的特征向量來決定下一層次各要素對上一層次某一要素的權重，并驗證其是否通過一致性檢驗。

①計算權向量：

將矩陣A的列向量歸一化：

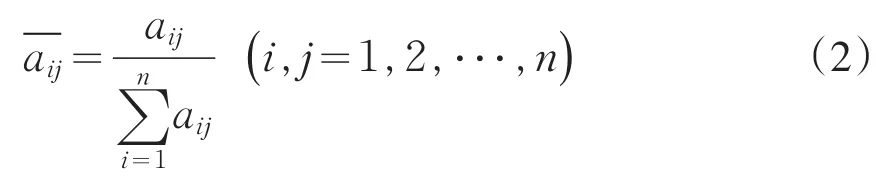
求歸一化處理后的矩陣各行元素之和：

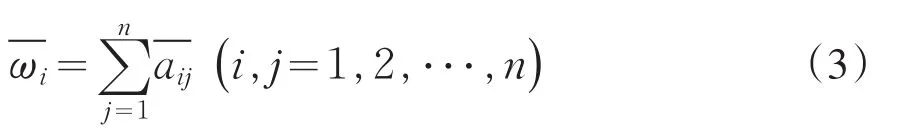
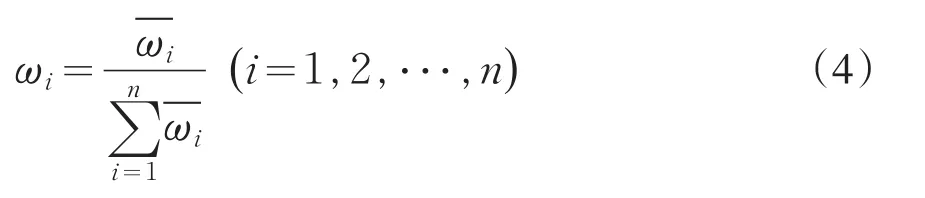
則ω=(ω1,ω2,???,ωn)T即為所求的權向量，且ω1+ω2+???+ωn=1

②一致性檢驗

計算λmax作為矩陣A的近似最大特征值：

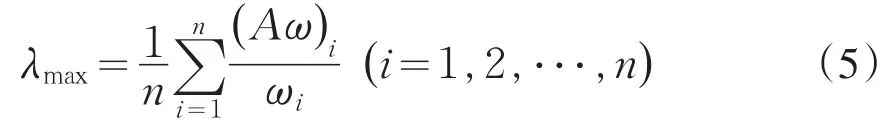
計算一致性指標CI：

根據表2可查出相應階數的隨機一致性指標RI。

計算一致性比率CR：

當CR＜0.1時，認為矩陣A的不一致程度在允許范圍以內，否則須對矩陣A進行調整使其滿足CR＜0.1。

（4）計算組合權向量并做組合一致性檢驗。計算結構模型的組合權向量，求出方案層各要素對目標層的權重，對方案層各要素進行優劣等級排序，并檢驗其一致性。

當方案層對目標層的組合一致性比率CR＜0.1時，認為整個層次的比較判斷通過一致性檢驗。

考慮到求解比較矩陣的特征向量和特征值等各項指標時，計算繁瑣且不精確，為此運用Matlab計算軟件進行計算，可以保證計算結果的準確性。采用此軟件只要輸入比較矩陣和相應的命令就可以得到各比較矩陣的權向量、方案層對目標層的組合權向量及其一致性比率等。

表2 隨機一致性指標RI的數值Table 2:Values of the random consistency index RI

3 案例應用

在龍脖水庫除險加固工程中，土料需求量為1.5萬m3，周邊主要有王營、張溝、塔羅以及王彥等土料場，因此通過層次分析法對上述料場進行優化選擇，以滿足工程的需要。

3.1 層次結構模型

對建筑材料土料進行選擇時，在保證質量的前提下，要充分考慮諸如土料的儲量、運距、開采費用以及環境保護等因素。儲量問題關系到能否滿足除險加固工程對土料的需求量，運距主要考慮運輸的距離、運輸的難易程度等，開采費用主要指剝離層的厚度、開采的難易程度等，直接關系到工程預算，而環境保護則是體現可持續發展的一個重要指標。建立層次結構模型見圖1。

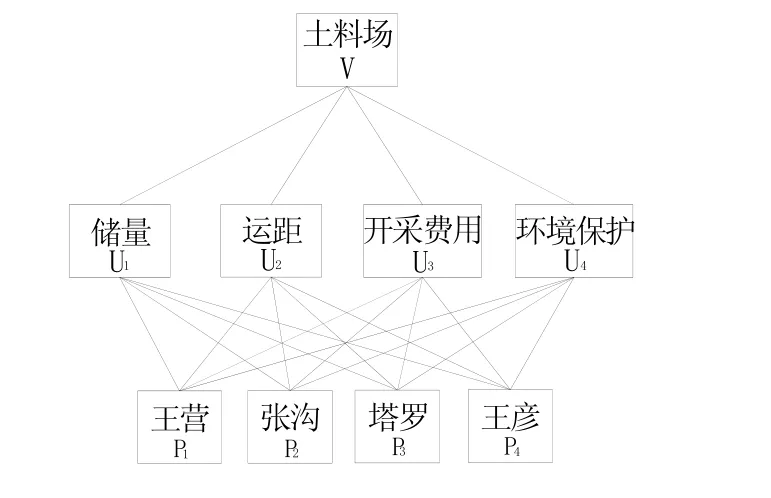
圖1 層次結構模型Fig.1 Hierarchical structure model

3.2 比較矩陣的構造及相關計算

料場選擇要滿足工程經濟預算、工期、工程質量和環境保護等方面的要求，通過業主單位和施工單位有關專家評定，對準則層的上述四個指標（即經濟預算、工期、工程質量和環境保護）相對于土料場的重要性進行兩兩比較，構造出比較矩陣，并計算出其權重，計算結果見表3。

儲量問題關系到能否滿足除險加固工程對土料的需求，王營、張溝、塔羅、王彥料場的土料儲量分別為 2.1 萬 m3、3.4 萬 m3、2.8 萬 m3、4.2 萬 m3。王彥土料場的料源儲量尤為明顯。建立比較矩陣見表4。

運距與包括運輸的距離、暢通情況等在內的許多因素有關。王營位于壩體右岸東北方向，距壩肩1 km；張溝位于壩體下游以南方向的山嶺上，距壩肩1.4 km；塔羅位于左壩肩北偏西方向，距壩肩2.8 km；王彥位于壩左岸以南山嶺上，距壩趾2 km。在土料場的選擇中，王彥、塔羅土料場距公路近，地勢平坦，運輸較方便；而王營、張溝土料場運輸較不方便。建立比較矩陣見表5。

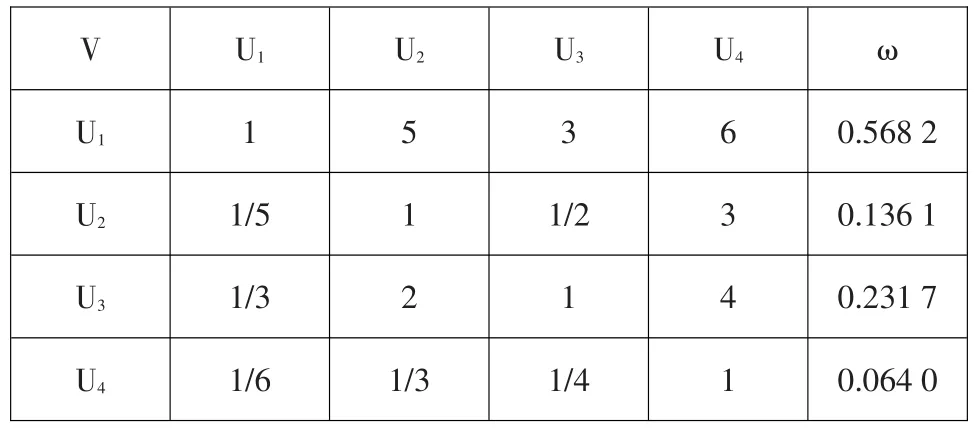
表3 土料場的比較矩陣V-U及權重Table 3:Comparison matrix of the soil yards V-U and weights

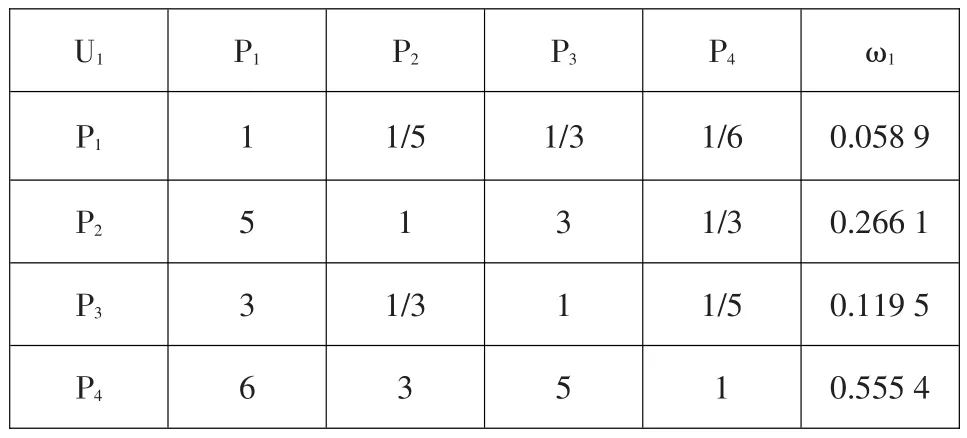
表4 儲量的比較矩陣及權重Table 4:Comparison matrix of the reserves and weights

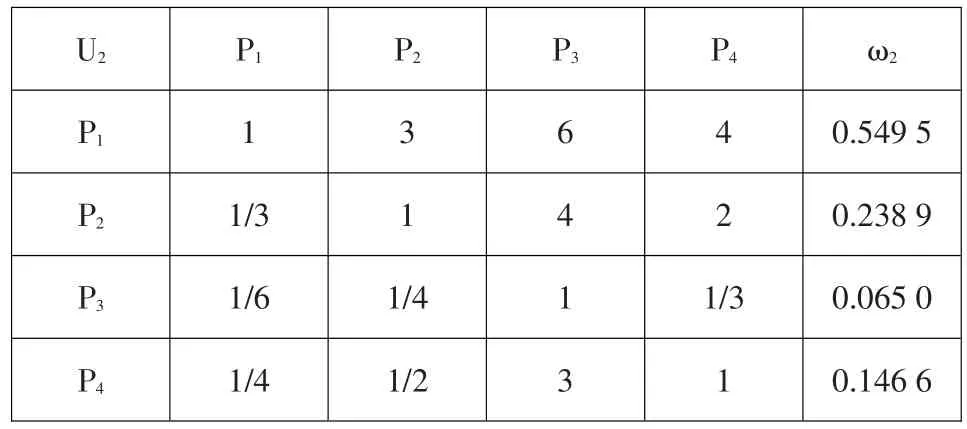
表5 運距的比較矩陣及權重Table 5:Comparison matrix of transport distances and weights

開采費用直接關系到工程預算，包括開挖的難易程度、剝離覆蓋層的費用、棄渣處理的費用等。王營料場高程在640～650 m之間，表層為腐殖土，厚度1 m；張溝料場高程在647～660 m之間，表層腐殖土厚0.8 m；塔羅料場高程在630～645 m，巖性為低液限粘土，表層腐殖土厚度1.3 m；王彥料場高程593～607 m，上覆耕植層厚約0.5 m。建立比較矩陣見表6。

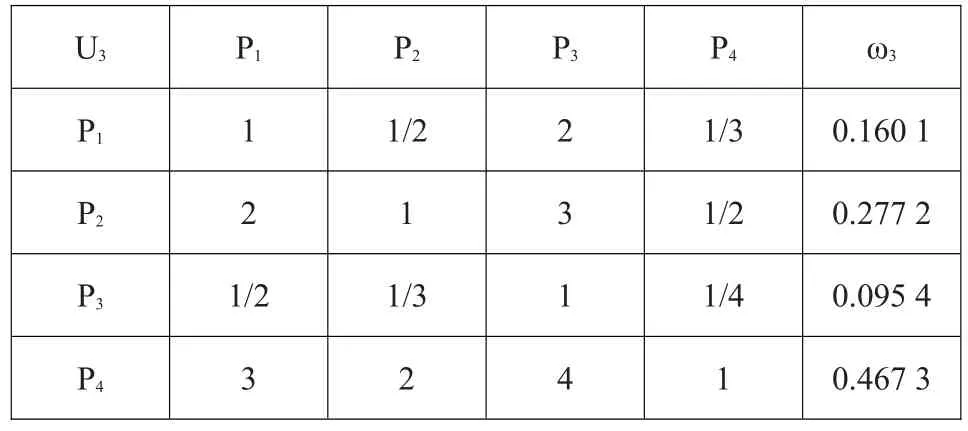
表6 開采費用的比較矩陣及權重Table 6:Comparison matrix of exploitation costs and weights

環境保護是體現可持續發展的一個參照指標，土料場開挖考慮的環境保護主要是覆蓋層剝離產生固體廢棄物等棄渣、后期的覆土、林地恢復防止水土流失等。建立比較矩陣見表7。

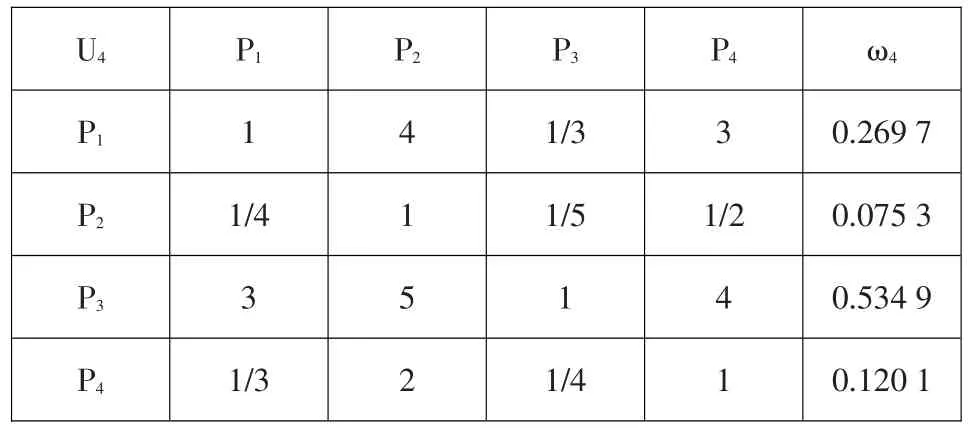
表7 環境保護的比較矩陣及權重Table 7:Comparison matrix of environmental protection and weights

以上準則層各比較矩陣的一致性比率CR的計算結果均小于0.1，滿足一致性檢驗，各ω值可作為權向量。

3.3 組合權向量及一致性檢驗

方案層的四個方案相對于目標層土料場的組合權向量計算及一致性比率結果見表8。

從表8的組合權向量可以看出，王營、張溝、塔羅、王彥四個土料場對總目標的權重值分別為0.162 6、0.252 8、0.133 1、0.451 5，其中第四個方案王彥料場在料場選擇中占的比重為45.15%，遠遠大于第一、二、三方案的比重，所以最能滿足對土料的需求，選擇該料場最為合適。

組合一致性檢驗：由Matlab計算程序得出CR=0.076 7＜0.1，通過了組合一致性檢驗，上述組合權向量計算結果可以作為最終決策的依據。

4 結 語

水庫除險加固工程的土料場選擇受土料儲量、開采費用、運距、環境保護等多種條件制約，在這些因素中既有儲量、開采費用、運距等可以定量的指標，又有環境保護等只能定性難以量化的指標。將系統的、層次化的、定性和定量相結合的分析方法——層次分析法引入到各項指標權重的確定中來，同時經過有關專家評定，從而大大減小了人的主觀因素的影響，最終選擇既滿足工程施工需要又經濟合理的料場方案，保證了決策的客觀性、科學性和合理性，為決策者提供了非常有參考價值的依據。

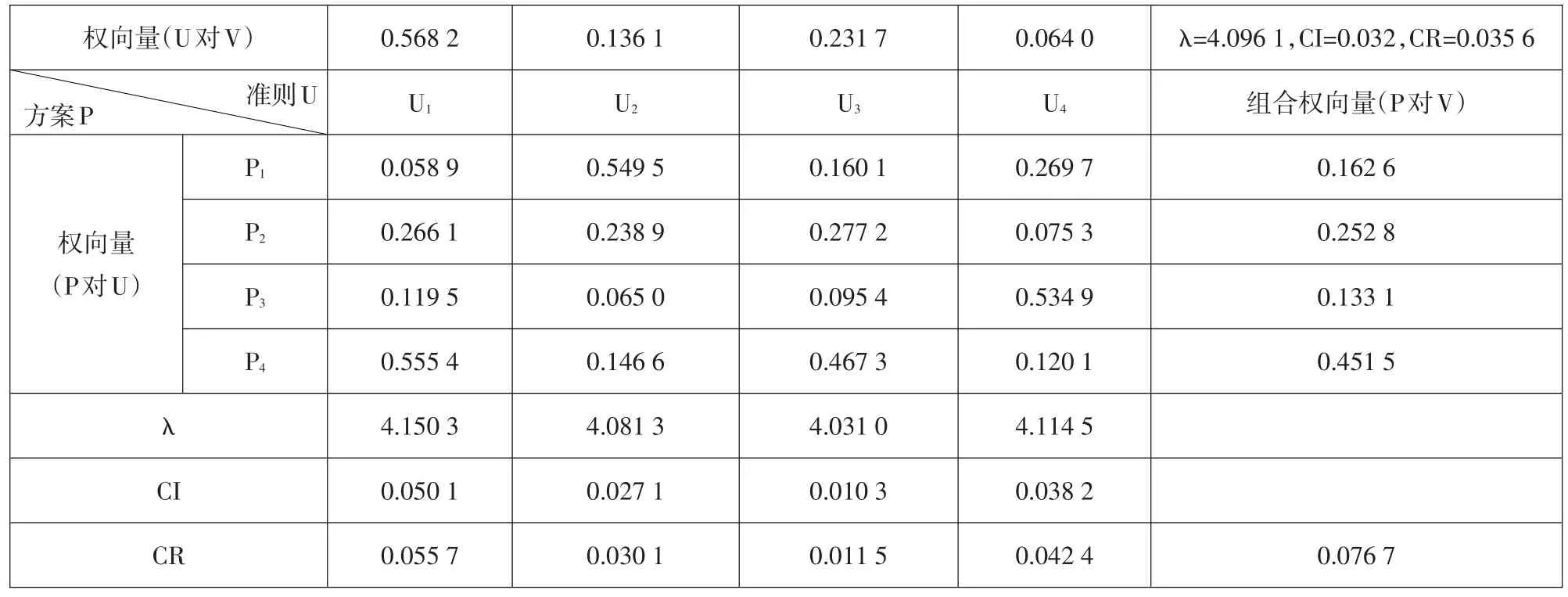
表8 以土料場V為目標的計算結果Table 8:Calculation results of the soil field V

[1]姜啟源.數學模型[M].北京:高等教育出版社,1993.

[2]李曉東,曾光明,梁婕.基于層次分析法的洞庭湖健康評價[J].人民長江,2009,40(14):22-25.

[3]楊波,唐德善,盧興旺.基于AHP的河道整治方案優選[J].水電能源科學,2010,28(2):109-110.

[4]張篤濤,郭天虎,董振旗.層次分析法在軍事風險投資項目中的應用[J].中國西部科技,2009,8(19):23-24.

[5]王力平.模糊層次分析法在實際工程中的應用[J].山西建筑,2009,35(23):209-210.