基于彈道計算的截斷誤差估計與補償

陳紅英,李輝芬,伍輝華,何 晶,吳 君

(中國衛星海上測控部,江蘇江陰214431)

0 引言

彈道測量數據事后處理的結果是作為型號試驗的精度分析、評定和性能改進、提高的重要依據,不斷改進測量數據處理方法和技術,提高彈道測量數據精度,對于提高海上測控水平和綜合試驗能力有重要意義。由于種種原因,外測系統的觀測數據總含有隨機誤差,必須通過相應的平滑與濾波處理,以減小隨機誤差的影響。但當彈道變化的曲率較大時,速度和加速度參數變化劇烈,微分平滑公式的誤差對計算結果的影響很大,會產生較大的截斷誤差。如何進行截斷誤差的補償、提高彈道參數的精度是數據處理中面臨的迫切問題。通過對截斷誤差補償原理和方法的介紹,采用理論彈道補償法對外彈道特征點前后數據進行了補償計算,分析了對彈道參數進行截斷誤差補償的有效性和可行性。

1 誤差原理分析

運載火箭的飛行過程極其復雜,為了降低隨機誤差的影響,擬合多項式的階數越低越好,觀測數據的總平滑點數越多越好。為此,輸入觀測數據的真實信號要用低階多項式來近似描述,這樣又會造成嚴重“失真”,另外在一定的觀測采樣頻率f下,參與平滑的觀測點數越多,則總的平滑區間T=N?h也越長,就需要用一個較高階多項式來描述。采用曲線擬合平滑微分方法計算彈道參數不可避免地會有截斷誤差,對于位置和速度變化劇烈的彈道段,更是存在較大的截斷誤差。例如級間分離段、關機段和再入段等彈道曲率較大,這也是人們比較關注的弧段,為能正確反映目標飛行軌跡,得到精確的彈道參數,必須對其進行修正補償。

根據彈道動態情況,實際數據誤差特性和所需精度要求,對非關機點附近的主動段彈道、自由段彈道和再入段彈道,位置數據一般采用1階或3階中心平滑,速度數據采用2階中心平滑,加速度數據采用3階中心平滑比較合適。平滑區間則根據彈道動態各外測系統的觀測數據采樣率來決定。對于中心平滑,假設輸入的觀測數據序列為xi,i=-n,-n+1,…,0,…,n,并且記中心平滑后輸出的中心點的估計值為于是輸入觀測數據與輸出數據的關系為:

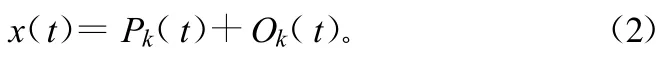
現將輸入觀測數據xi關于中點i=0做k階泰勒展開,并用積分形式表示其余項,則

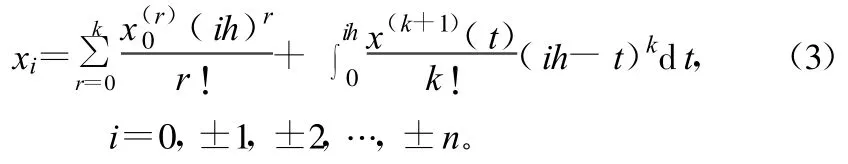
將輸入觀測數據的泰勒展開式代入中心平滑公式,那么濾波輸出數據為:

由wi的性質可將式(4)變為:

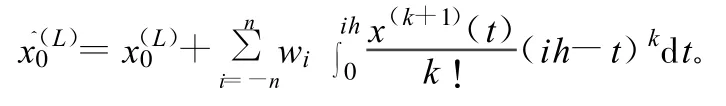
式中,第1項為中心點i=0真實信號的L階導數,而是中心平滑后輸出的數據。可以看出和相等的充要條件是上式右邊第2項為零,也就是只有輸入觀測數據的真實信號x(t)為k階時間多項式,余項的濾波結果才能為零。或者說,x(t)是高于k階的時間多項式,則中心點濾波后的就有誤差。令

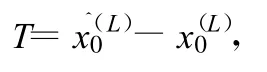
并稱T為k階多項式中心平滑的截斷誤差。

2 補償方法

截斷誤差補償方法常用理論彈道補償法和外遙聯合補償法,另外還有截斷誤差函數補償法。

2.1 理論彈道補償法

假若有理論彈道數據X和,則事先可由理論彈道的坐標數據X用微分平滑方式計算出t時刻的速度值,再將t時刻的理論速度值X與做差,得到該時刻的截斷誤差估計量為處理時把作為實測數據微分得到的的補償值,該方法稱為理論彈道補償法。對于加速度微分平滑也可按同樣原理處理。但應注意的是,實際彈道與理論彈道是有差別的,必須把特征點對齊后,再由此向特征點前后進行相應的補償。

2.2 外遙測聯合補償法

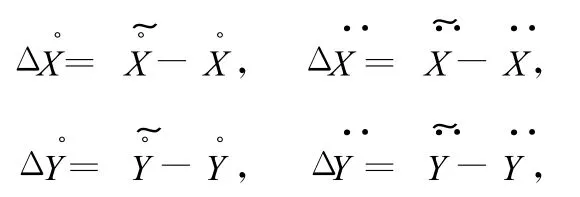
視為截斷誤差,加到對應的外測所得到的速度和加速度上進行補償,該方法稱為外遙測聯合補償法。具體計算步驟如下:

①由遙測過載參數nx、ny和程序俯仰角φ計算

③根據前述的原理得到對應量的截斷誤差補償值。

2.3 函數補償法

構造截斷誤差補償函數Ri(n,p)。假設ti的速度真值為,微分值為對應的截斷誤差為Ri(n)。顯然,截斷誤差與點數n有關。假設在同一時刻ti,取n=k,k+1,…k+L,則由微分公式可得一系列計算速度值和L均為正整數。于是有:

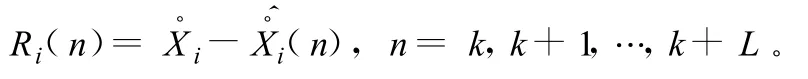
當采樣間隔h確定后,截斷誤差隨n的增大而增大,而同一時刻的是確定的常數。因此隨n的增大而遠離反之則接近在O-n坐標系中,以n為自變量,并用最小二乘擬合法求出擬合曲線Ri(n,p),其中p為曲線的階數。即設

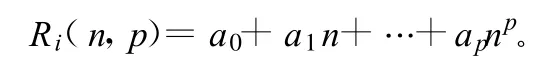
式中,待定常數ai在K、L、P給定時,由最小二乘法求得,并稱Ri(n,p)為誤差補償函數,用它作為的近似值,相當于對的補償。

3 應用效果分析

綜合考慮上述3種截斷誤差補償方法的優點和局限性,在短時間內采用理論彈道補償法對外彈道測量數據進行誤差補償。

在測量船某型號任務R中,將理論彈道數據資料進行整理,并對火箭運行過程各特征點數據進行了截斷誤差的補償,具體方法是利用理論時刻的加密彈道對實際特征點時刻前后若干點的彈道數據進行補償,其中包括X、Y、Z方向的速度x?和加速度x

¨處理數據,彈道傾角、偏角,切向、法向和側向加速度等。根據理論彈道補償法的原理,對齊特征點是補償的重要步驟。

表1中列出了某型號任務R在特征點A時刻T(相對時1 100 s)X方向速度和加速度前后補償結果的部分數據。

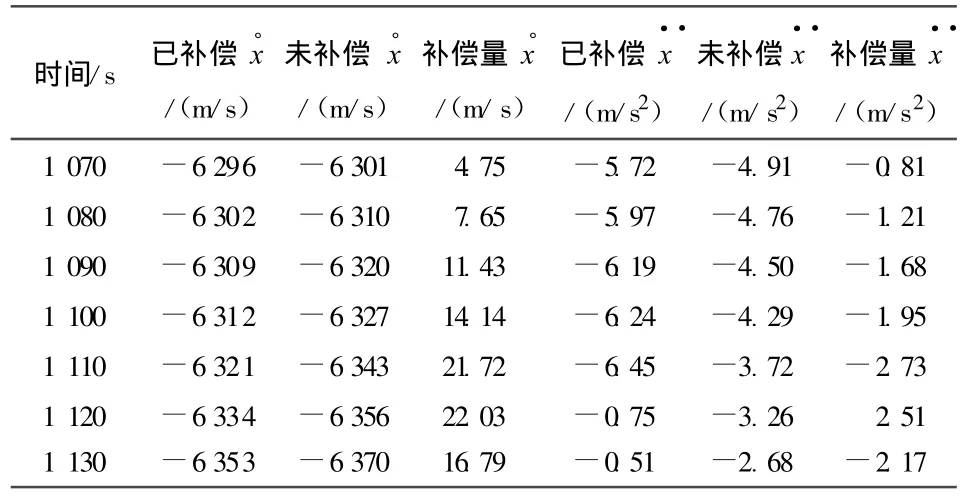
表1 特征點A時刻前后數據補償情況

從表1中可以看出在特征點A附近補償量數據變化激烈,補償量明顯變大。

由于速度數據采用2階中心平滑,加速度數據采用3階中心平滑,實戰任務R中補償前的數據做了平滑處理,而截斷誤差補償后的特征點A和特征點B時刻X方向速度和加速度數據變化情況如圖1和圖2所示。

圖中2條曲線分別為未做誤差補償和已做誤差補償的曲線,從圖1和圖2可以看出,任務時間段內整個曲線的變化趨勢,在2個特征點時刻曲線發生明顯跳變,通過對特征點時刻局部放大,可以更加清楚地看出補償量的大小,這也驗證了在特征點時刻截斷誤差較大的理論。

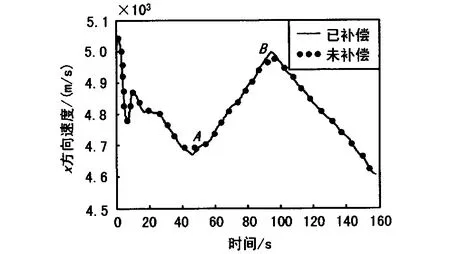
圖1 各特征點時刻X方向速度截斷誤差補償

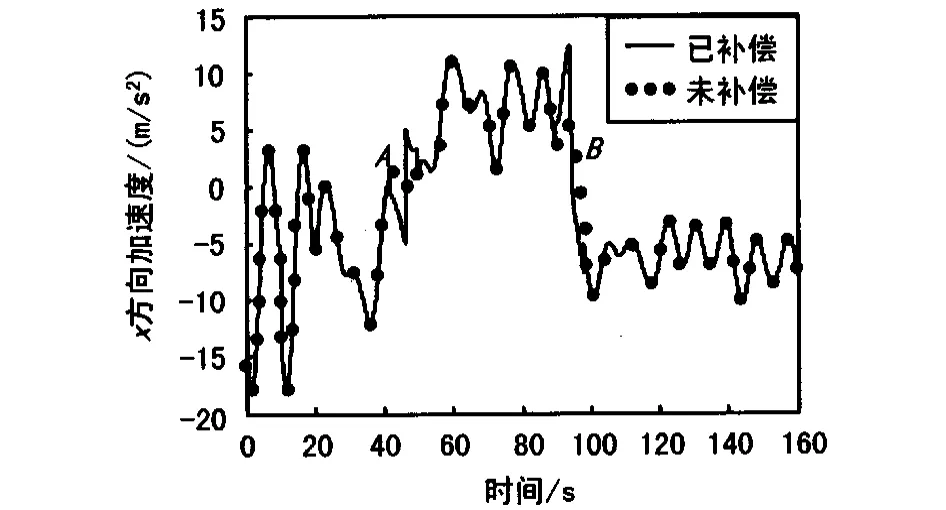
圖2 各特征點時刻X方向加速度截斷誤差補償

對火箭運行過程中位置和速度曲率較大的特征點參數進行誤差補償,真實地體現了目標的飛行軌跡,得到較為精確的彈道參數,證實了對特征點時刻參數作截斷誤差補償的必要性。

4 結束語

采用理論彈道對速度和加速度等彈道參數進行截斷誤差補償,取得了明顯的效果,從計算的結果可以看出,在特征點利用理論彈道對參數進行截斷誤差補償,其計算精度遠遠高于通過微分坐標求解的結果精度,該方法的成功運用大大提高了彈道參數的處理精度,為不斷提高測量船海上測控任務數據處理方法和技術提供了重要依據,也被應用于測量船后續的各種任務中用于獲取高精度的雷達等外測設備的彈道參數數據。

[1]劉利生.外彈道測量數據處理[M].北京:國防工業出版社,2002.

[2]張忠華,李曉勇.船載設備動態測量數據的建模與參數估計[J].無線電工程,2008,38(5):13-17.

[3]柴 敏.運載火箭外測彈道截斷誤差的潔化插值修正算法研究[J].航天控制.2009(5):10-14.