初始幾何缺陷對大跨度鋼桁架吊裝穩定性影響

李 匯 王學國 何國武

1 概述

隨著各種新型復雜大跨度鋼結構建設項目的增多，人們對大跨度鋼桁架的施工技術及施工過程中表現出的諸多力學及技術問題愈來愈重視[1，2]。然而，大跨度鋼桁架在吊裝過程中的受力狀態與設計分析中的狀態截然不同。為確保大跨度鋼桁架在吊裝過程中的安全性，在整個施工吊裝過程中都不允許發生屈曲失穩。屈曲不僅會使大跨度鋼桁架發生過大的變形，而且往往會導致結構的失穩破壞[3，4]。線性屈曲理論對結構穩定性進行分析時，是基于初始有限變形及線彈性的假設，沒有考慮結構受載后的變形和幾何初始缺陷對平衡狀態的影響[5]。由于鋼結構構件往往存在著各種不同大小的初始缺陷，常以極限型屈曲形式失去穩定，因此有必要進行初始幾何缺陷對大跨度鋼桁架吊裝的穩定性影響分析。

2 大跨度鋼桁架吊裝有限元模型

以某大型復雜體系鋼結構的大跨度鋼桁架構件的吊裝來進行實例分析，模型如圖1所示。該平面桁架總長30 m，總共7跨，中間節間距為5 m，兩端節間距為2.5 m，左端高1 m，右端高3 m，吊裝過程中吊索采用直徑為38 mm的鋼絲繩起吊，考慮了兩吊點和四吊點兩種吊點方案。

基于大型有限元分析軟件ANSYS，建立了大跨度鋼桁架吊裝有限元模型，各弦桿和腹桿均采用Beam188單元，吊索采用Link8單元。結構所受荷載為鋼桁架自重，考慮到吊裝過程的動力效應，取1.2倍的動力系數，即屋架吊裝過程中受到1.2g的重力作用(g為重力加速度)。

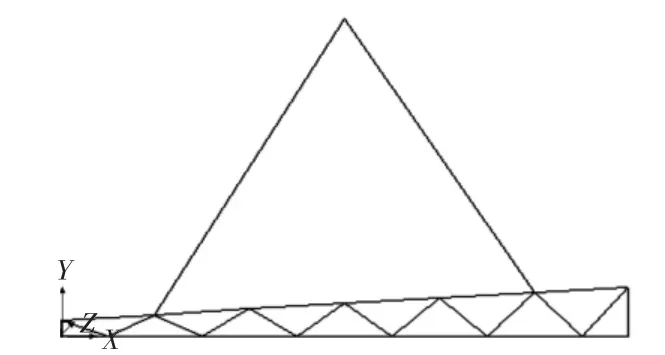
圖1 某大跨度平面鋼桁架示意圖

3 考慮初始缺陷的非線性屈曲分析

3.1 兩吊點方案

進行非線性屈曲分析時，考慮到特征值屈曲的第一階屈曲模態最容易發生，因此在進行非線性屈曲分析之前，可以先經過特征值屈曲分析，得出鋼桁架在吊裝過程中的第一階屈曲模態。兩吊點方案的特征值屈曲分析的第一階屈曲模態如圖2所示。

分析兩吊點屈曲模態可知，第一階屈曲模態體現為鋼桁架跨中部分出現平面外變形，且以10號和11號桿件最為嚴重。因此容易判斷在吊裝過程中跨中上弦桿部分容易發生平面外失穩。進行非線性屈曲分析時，取第一階屈曲模態變形的1/1000作為原屋架的初始幾何缺陷，圖3給出了10號桿件隨10號和11號相連處在Z向在平面外位移發展的軸力—位移曲線圖，在1.2g的重力作用下，10號桿件隨10號和11號相連處在Z向在平面外位移發展的軸力—位移曲線為線性變化，說明該鋼桁架結構還沒有達到極限狀態，即此時鋼桁架不會發生平面外屈曲。再將鋼桁架所承受1.2g重力荷載乘上第一階屈曲因子2.78，即讓屋架承受3.3g的豎向荷載作用，再次進行非線性屈曲分析。圖4給出了3.3g豎向荷載作用下10號桿件隨10號和11號相連處在Z向在平面外位移發展的軸力—位移曲線圖。在3.3g豎向荷載作用下該大跨度鋼桁架在平面的位移已經發展的很大，發生了平面外失穩。在施工過程中豎向荷載工況發生改變時，可以按照上述方式對兩吊點方案進行針對性的非線性屈曲分析。

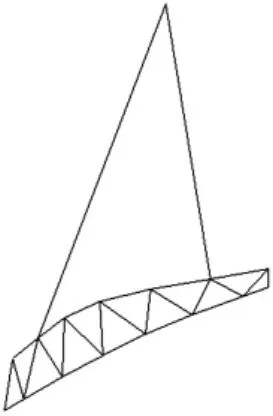
圖2 兩吊點方案的第一階屈曲模態

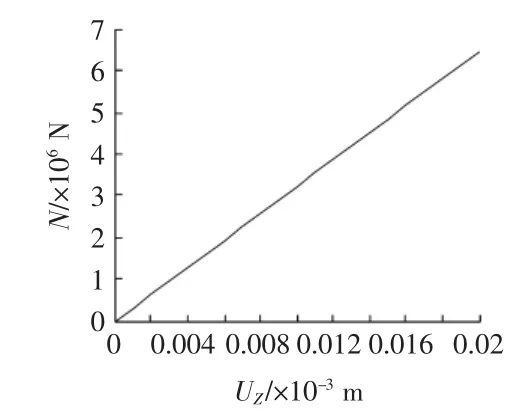
圖3 10號桿件軸力—位移曲線（1.2g）

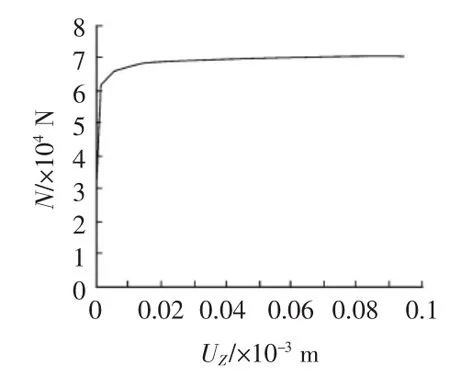
圖4 10號桿件軸力—位移曲線（3.3g）

3.2 四吊點方案

四吊點方案的特征值屈曲分析的第一階屈曲模態如圖5所示。

圖5 四吊點方案的第一階屈曲模態

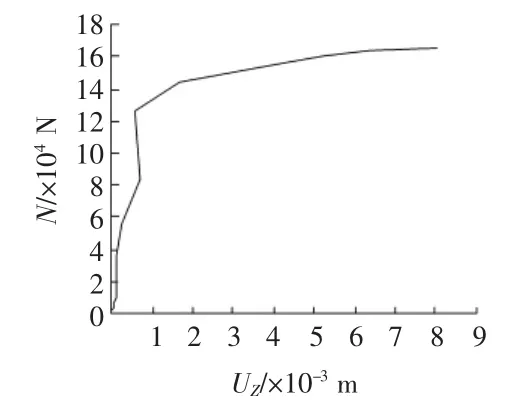
圖6 2號桿件軸力—位移曲線（18.88g）

分析四吊點方案屈曲模態可知，第一階屈曲模態體現為鋼桁架跨中部分出現較小的平面外變形，且以2號和3號桿件變形最大。因此容易判斷在吊裝過程中跨中下弦桿部分容易發生平面外失穩。從屈曲特征值來看，兩吊點情況下第一階屈曲特征值為2.78，四吊點情況下15.73，顯然四吊點方案的第一階屈曲模態較之兩吊點方案很難出現，這表明四吊點方案顯著提高了大跨度鋼桁架吊裝過程的平面外穩定性。

下面將鋼桁架所承受1.2g重力荷載乘上四吊點方案的第一階屈曲因子15.73，即讓屋架承受18.88g的豎向荷載作用，進行非線性屈曲分析。圖6給出了2號桿件隨2號和3號相連處在Z向在平面外位移發展的軸力—位移曲線圖，圖中所示的情況在實際中鋼桁架吊裝中也不可能存在，因為吊裝時鋼桁架不可能受到如此大的豎向荷載作用，但可以看出在18.88g豎向荷載作用下該大跨度鋼桁架在平面的位移已經發展的很大，發生了平面外失穩。因此，在施工過程中豎向荷載工況發生改變時，可以按照上述方式對四吊點方案進行針對性的非線性屈曲分析。

4 結語

基于大型有限元計算程序ANSYS對大跨度鋼桁架吊裝進行了初始幾何缺陷對大跨度鋼桁架吊裝的穩定性影響分析。在兩吊點方案中容易發生屈曲的位置為跨中上弦桿部分，而四吊點方案在吊裝過程中跨中下弦桿部分較易發生平面外失穩，這由于多吊點方案改善了吊裝過程中構件的受力狀況，從而提高了大跨度鋼桁架吊裝過程的平面外穩定性;非特征值屈曲可以一直進行到結構的極限荷載，可更準確的預測屈曲荷載。非線性屈曲分析得到的臨界載荷小于同樣條件下的線性分析特征值，這是由于結構初始缺陷及應變非線性的影響作用所致。對于一個復雜的結構體而言，即使結構內部局部發生了屈曲，但整體結構仍然可以繼續承載。若要找到結構的垮塌屈曲值，只能進一步增加載荷進行分析。

[1]郭彥林，崔曉強.大跨度復雜鋼結構施工過程中的若干技術問題及探討[J].工業建筑，2004，34(12):1-5.

[2]Nuno Silvestre，Dinar Camotim.Elastic Buckling and Second-Order Behaviour of Pitched Roof Steel Frames[J].Journal of Constructional Steel Research，2007，63(6):804-818.

[3]Lluís Gil，Antoni Andreu.Shape and cross-section optimisation of a truss structure[J].Computers ＆ Structures，2001，79(7):681-689.

[4]梁 珂，孫 秦.加筋壁板結構非線性屈曲數值分析研究[J].航空計算技術，2008，38(3):49-51.

[5]S.L.Chan，S.H.Cho.Second-order analysis and design of angle trusses Part I:Elastic analysis and design[J].Engineering Structures，2008，30(3):616-625.