延遲復雜動態網絡的穩定性研究

李濤 于曉楠

1沈陽理工大學 遼寧 110168 2大連海事大學 遼寧 116023

0 引言

目前，復雜網絡的整體動力學行為和整個網絡的拓撲結構的相互作用的研究引起廣泛的關注。研究復雜網絡的最終目的是要了解網絡的結構如何影響網絡的動力學行為，以及反過來網絡的結構如何受動力學影響，復雜網絡的牽制控制及其穩定性分析就是其中一項重要的研究內容。在控制一個復雜網絡達到某一穩定狀態時，牽制控制是一種十分經濟實用的控制策略。特別是通過對網絡中的少數節點施加線性誤差反饋控制將網絡穩定到一個均勻的平衡點狀態，即是網絡中的每個節點的狀態都穩定到單個節點的平衡點上。一個很有趣的結論就是僅僅控制網絡中的任何一個節點，就可以將整個復雜動態網絡控制到這樣一個均勻的平衡點狀態。

1 預備知識

考慮一個由N個相同的線性分散耦合節點構成的延遲復雜動態網絡，其中每個節點都是一個n維的動力學系統。第i節點的狀態方程為：

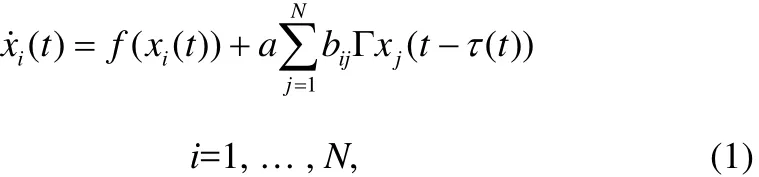
這里x(t) = (x(t),x(t) , L ,x(t) )T∈Rn是第i個節點的狀

ii1i2in態向量，常數τ(t)＞0代表延遲函數。f(·)是一個描述節點動力學特性的連續可微的向量函數，常數a＞ 0 是網絡的耦合強度。常數對稱矩陣 Γ = （γ）∈Rn×n是各個節點狀態變量ij之間的內部耦合矩陣，這里假設每個節點的內部耦合矩陣是完全相同的。耦合矩陣B= (bij) ∈RN×N代表網絡的拓撲結構，若節點i和j(j≠i)之間有連接，則bij=bji= 1 ；否則bij=bji= 0 。在本文的模型中，耦合系數滿足如果節點的度ki定義為與第i個節點連接的邊的數目，則

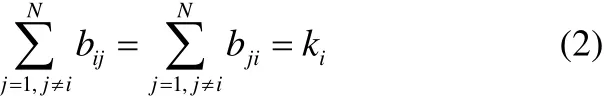
我們的目標是使網絡達到一個穩定狀態，也就是當t→∞時

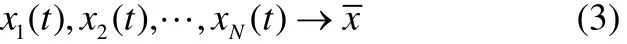
這里是孤立節點的平衡點，滿足條件

為了實現目標(4)我們選擇控制網絡中的部分節點來達到控制整個網絡的目的。不失一般性，我們選擇前l個節點作為被控節點，l是Nδ的整數部分。

因此，該被控網絡的第i個節點的狀態方程為：

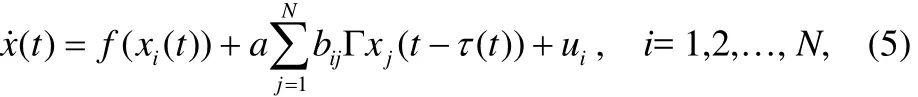
該系統的局部負反饋控制器的方程為：

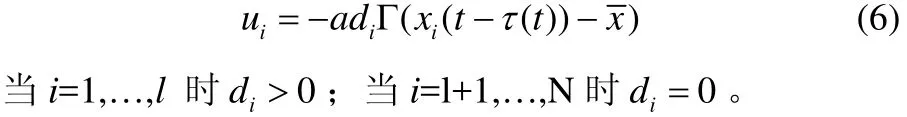
本文考慮的是無向網絡，同時我們假設網絡(1)是連同的。從而我們得到耦合矩陣B是一個不可約的實對陣矩陣，即T

BB= 。對于本文中其他部分，我們作出如下假設：

假設 1.()tτ是一個可微函數，滿足下列條件：

引理1. 如果一個實對稱不可約矩陣B= (bij) ∈RN×N滿足下列兩個條件：

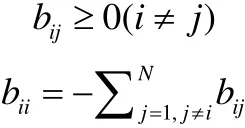
則有：

(a) 0是矩陣 B的最大特征值且對應的特征向量為[1,1, ,1]T

L ；

(b) B的其它特征值都是負實數；

(c) 存在一個非奇異矩陣

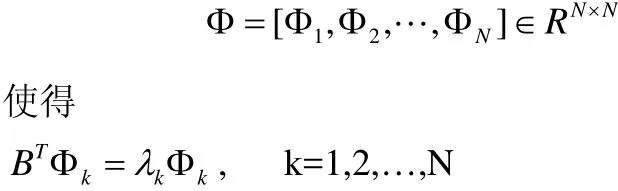
這里 0 =λ1＞λ2≥λ3≥ L ≥λN是矩陣B的特征值。

引理2.如果矩陣B符合引理1中的定義，非零對角矩陣D定義如下：

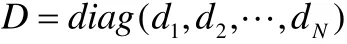
這里di≥ 0 (i= 1 , 2,L ,N)，

則C=B-D是負定矩陣。

引理3.假設

Q(x) =QT(x)、R(x) =RT(x)線性矩陣不等式

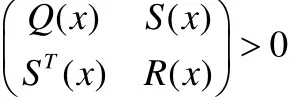
與下面的條件之一等價：

(a)Q(x) ＞ 0 ,R(x) -ST(x)Q-1(x)S(x) ＞ 0

(b)R(x)＞ 0 ,Q(x) -S(x)R-1(x)ST(x) ＞ 0

2 帶有時變延遲的復雜動態網絡的牽制同步判據

定理1.如果下列N個微分方程

η˙k(t) =J(t)ηk(t) +aλkΓηk(t-τ(t)), i=1, 2, …, N, (8)

關于其零解漸進穩定，則被控網絡(5)能夠達到局部漸進穩定。

這里J(t) ∈RN×N是f(xi(t))在s(t)附近估計的 Jacobian矩陣。

證明. 定義誤差系統ei=xi(t) -x,i=1, 2, …,N，則有

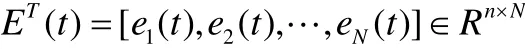
由于f(xi(t))是連續可微的，將被控網絡(5)在平衡狀態附近線性化，得到；

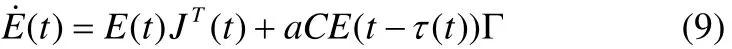
這里J(t) ∈Rn×n是f(xi(t))在x附近估計的 Jacobian矩陣，且C=B-D，D=diag(d1,d2, LdN)。

由引理1和引理2知C是負定對稱矩陣，所以可知C的特征值是嚴格的小于零的，其特征值定義如下：

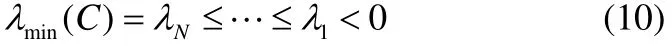
其相對應的特稱向量為：

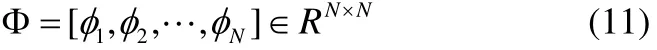
滿足：

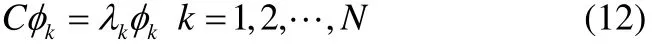
定 義η(t) = (η1(t) ,η2(t) , L ,ηN(t))，基 于 特 征 向 量{φ1,φ2,L ,φN}，我們可以得到：

于是由(9)和(13)可得如下的等式：

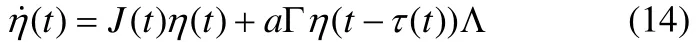
這里 Λ =diag(λ1,λ2,L ,λN)，所以我們只需要使下列N個微分方程：

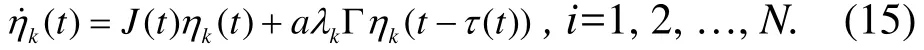
關于其零解漸進穩定，則被控網絡(5)能夠達到局部漸進穩定，證畢。

最后指出：這里我們將(N×n)維的非線性系統(5)的局部穩定性問題轉化為N個獨立的m維的線性系統(8)的穩定性問題。

下面的定理給出了復雜網絡關于平衡狀態x的局部漸進穩定的充分條件。

定理2.如果存在矩陣P＞ 0 ，Q＞ 0 ，R＞ 0 ，M＞ 0 和適當維數的矩陣N1，N2滿足下列條件：

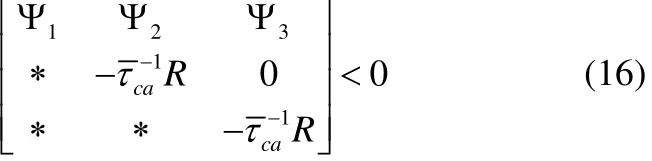
則被控網絡(5)能夠達到局部漸進穩定。

這里

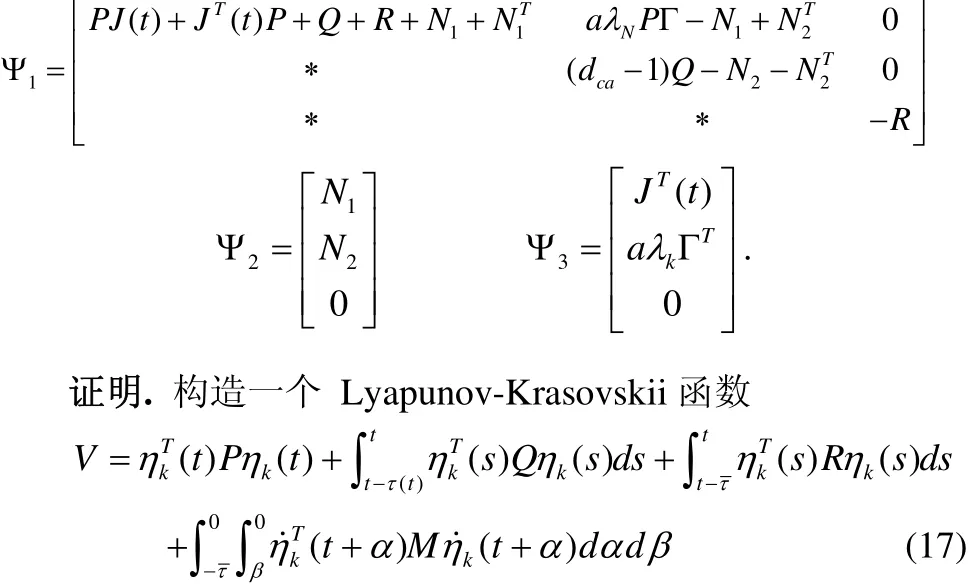
則有：

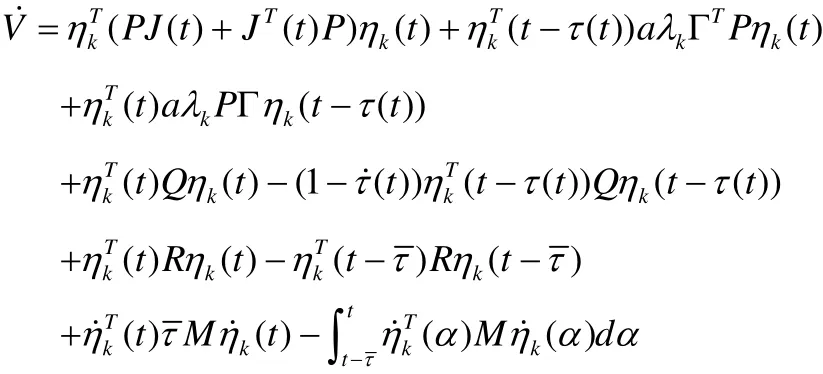
由Newton-Leibniz 公式可得下面的公式：

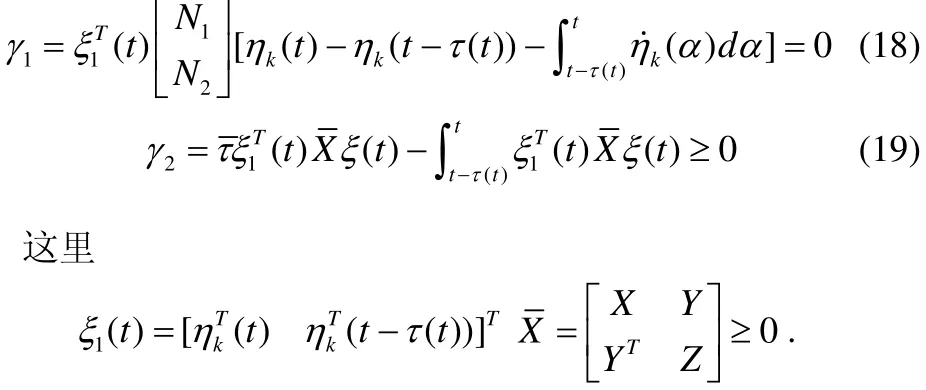
那么下面我們可以得到

則我們可以知系統(8)局部漸進穩定。

由引理3，可知式(23)等價于下式：

通過引理3，由式(22)和(24)我們可以得到以下的穩定性條件：

再由引理3知條件(11)與條件(25)等價，所以0V＜˙，也就是說被控網絡(5)能夠達到局部漸進穩定。

3 仿真實例

為了驗證前面得到的理論結果，下面我們以三維非線性系統為節點構成的網絡為例進行分析。這里我們只選擇具有代表性的BA無標度網絡進行仿真。

我們取平衡狀態x= [ 0 0 0]T考慮全狀態耦合矩陣Γ=diag(1 1 1)，則整個被控網絡可以描述為：

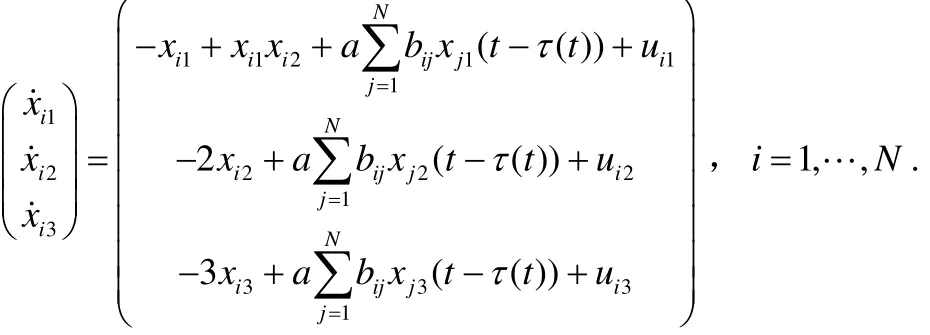
設計如下的狀態反饋控制律：

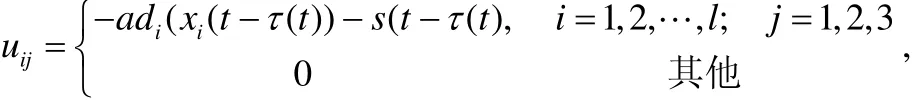
在下面的仿真研究中，考慮耦合時延τ(t)=sin(t)+1選擇了網絡規模有 50個節點(N=50)，初始值一致分布在區間[-1 1]內的BA無標度網絡。根據定理的結論，可求得耦合強度0＜a＜0.08。

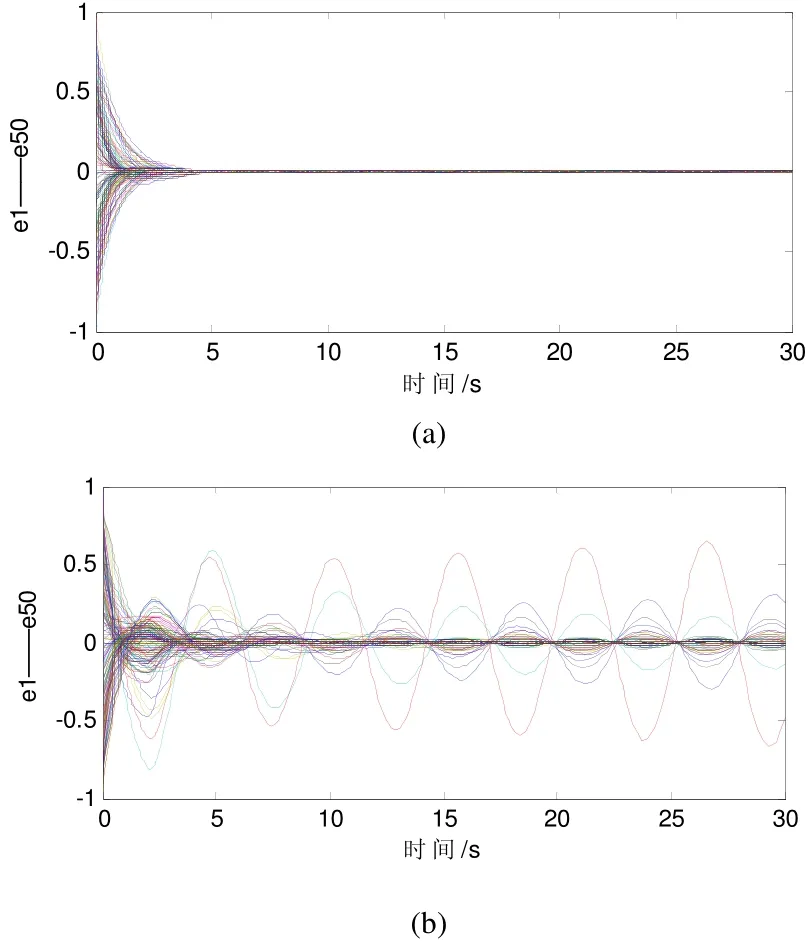
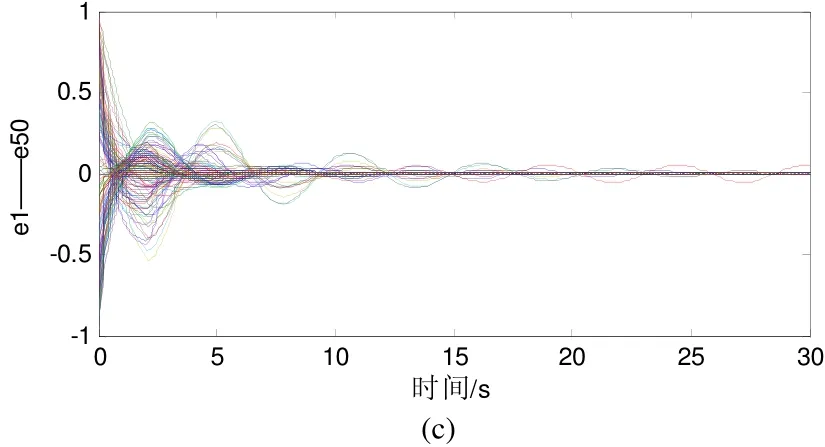
圖1 無標度網絡在 0.09a= 時的狀態變化圖

圖1(a)和(b)給出了不同的耦合強度對應的網絡節點的狀態變化圖。當 0.02a= 時滿足穩定條件，網絡能夠達到穩定狀態；當 0.09a= 時不滿足穩定條件，網絡不能達到穩定狀態。所以說耦合強度過大反而會破壞網絡的穩定性；而對于無延遲網絡來說，隨著耦合強度的增大網絡的穩定性能會增強。

圖 1(a)是在 0.09a= 時牽制控制度最大的節點時的控制效果圖，從圖1(b)中可以看出在未施加控制時網絡不能達到穩定狀態；而在牽制其中一個度最大的節點后，網絡能夠很快的達到穩定狀態。這說明特定牽制控制BA無標度網絡的一個節點就能達到很好的控制效果。

4 總結

本文主要研究了帶有時變延遲的復雜動態網絡的穩定性問題，得到了與時間相關的穩定條件。選擇的 Lyapunov-Krasovskii函數能夠充利用這個延遲量的信息，降低了所得穩定條件的保守性。所用的方法主要是在平衡點附近進行了線性化處理，同時將網絡相互關聯的N個動力學系統解耦為N個獨立的動力學系統，使得網絡復雜的動力學特性變得容易處理。在此基礎上，我們對每個獨立的系統進行分析，得到確保整個網絡達到穩定狀態的充分條件。本文的研究還表明：復雜的網絡節點的動力學特性、節點之間的耦合強度、內部的耦合矩陣、節點的耦合特征矩陣和牽制反饋增益等共同決定著復雜網絡的穩定性能。

[1]D.J. Watts, S.H. Strogatz, Collective dynamics of ‘small world’ networks.1998.

[2]A.-L. Barabási, R. Albert, Emergence of scaling in random networks.1999.

[3]X.F. Wang, G. Chen, Synchronization in scale-free dynamical networks: Robustness and fragility, IEEE Trans. Circuits Syst.2002.

[4]Xiang J, Chen, G R. On the V-stability of complex dynamical net works. Automatica.2007.

[5]Liu Z X, Chen Z Q, Yuan Z Z. Pnning control of weighted general complex dynmical networks with time delay. Physica A.2007.

[6]Zhou J, Lu J, Lü J. Pinning adaptive synchronization of a general complex dynamical network. Automatic.2008.