穩態加速度模擬試驗設備：離心機設計（10）

賈普照

（北京衛星環境工程研究所，北京 100094）

本篇對離心機進行一般性理論探討和結構設計分析，提出總體設計計算方法及總體構造與部件結構的設計建議，是離心機設計的核心部分。

本篇對離心機設計所作的分析與歸納均屬首次，因此也是一次嘗試，對離心機設計如果能起到提綱挈領、拋磚引玉作用，筆者就感到很欣慰了。

本篇不準備深入探討離心機復合環境問題，包括與振動臺復合及多軸載人離心機運動復合等專題性較強的內容。

本篇所提供的內容主要是作為離心機主機的一般設計計算方法，重點在于其獨特的總體設計與主機機械結構部分，即其非標準設計部分；至于電氣、液壓、監測、控制以及機械零部件的具體設計計算，讀者可從專業書籍和手冊獲得相應計算方法；匯電環、旋轉接頭、制動器、標準減速器、電動機及其驅動系統、液壓傳動系統、監測控制元器件等等也可獲得商品供應。

在總體設計中，氣動功率計算含有一定的實驗與經驗成分，各家有各家處理之道；總體布局與部件結構更是紛繁雜陳、琳瑯滿目，本文既不可能窮盡所有結構，也不會予以劃一。做法是：針對不同設計理念，根據手頭資料盡量展示、充分介紹，首先使資料集中呈現出來；期冀在資訊通達基礎上，逐漸摸索出某種規律性的東西，因為規律本身就反映了一種認知；在闡述和分析過程中，也會直接或間接地表達筆者體會或解決辦法，以供讀者參考；同時，也留存了一些供讀者探索與創新的空間。

為了系統觀察所討論的主題，在總體與部件結構分析時，會將有關資料予以不同的歸納與組合，不可避免地與“中篇（上）”部分內容特別是部分圖片有所重復，但其擔當角色各有側重，好處是使讀者在單獨閱讀某一章節時，能形成一個完整體系，同時免去前后翻閱之苦。

第6章 離心機力學分析及特性分析

目 錄

引言

6.1 單軸轉動離心機

6.1.1 單軸離心機運動學

6.1.2 單軸離心機動力學

6.2 雙軸轉動離心機

6.2.1 雙軸離心機運動學

6.2.2 雙軸離心機動態過程

6.2.2.1 雙軸載人離心機的啟動

6.2.2.2 座艙滾轉與重力加速度

6.2.2.3 座艙滾轉與切向加速度

6.2.2.4 座艙滾轉與科氏加速度

6.3 三軸轉動離心機

6.3.1 三軸離心機的啟動

6.3.1.1 從靜止啟動

6.3.1.2 從1G啟動

6.3.2 座艙俯仰運動

6.3.2.1 座艙俯仰運動方程

6.3.2.2 座艙俯仰角速度及角加速度

6.3.2.3 座艙俯仰過程的運動學描述

6.3.3 座艙運動與科氏加速度

6.4 離心機附加振動臺

6.4.1 附加單向振動

6.4.2 附加雙向振動

6.4.3 振動臺對離心機的影響

6.5 離心機力學分析小結

6.6 離心機基本特性

6.6.1 離心機加速度場的不均勻性

6.6.1.1 加速度數值的不均勻性

6.6.1.2 徑向加速度的輻射性

6.6.2 離心機試驗的固有誤差

6.6.2.1 法向加速度梯度誤差

6.6.2.2 側向加速度梯度誤差

6.6.3 離心機試驗的力學本質

引言

離心機是一個高速旋轉的大型機械設備，當旋轉同時再復合直線或其他圓周運動時，結構和分析將變得比較復雜。但不管如何復雜，其基礎平臺都是單自由度轉動運動形式，因此我們將從基本運動形式和基礎架構說起。

一般航空航天物體離心機只圍繞主軸進行單自由度轉動，此類離心機可稱為單軸轉動離心機；載人離心機則至少需具備可甩動的單軸艙，與大多數土工離心機需具有擺動式吊籃一樣，呈雙軸轉動形態，可稱為雙軸轉動離心機；掛有兩軸常平架的載人離心機，則為三軸轉動離心機；動態飛行模擬器至少有三條軸、甚至是四軸轉動的形態。

在各種轉動形態中，有的在吊籃或座艙內還附加了單向振動臺或雙向振動臺等直線位移裝置，呈多自由度復合運動形式。但迄今為止，從數量上說，還是單軸轉動和雙軸自由甩動吊籃（或座艙）的離心機最多，它們附加振動臺以后，通常也不把振動位移考慮在內。因此，對單軸離心機進行基本運動分析，大致可了解絕大多數離心機的情況，同時也是研究復合轉動運動的基礎。

對于三軸以上的運動復合，尤其當考察點偏離幾何中心，具有偏重或附加長沖程直線運動的情況，需要專題進行分析研究，本文將不涉及。

本章利用基本力學和數學分析工具，通過舉例分析，重點討論離心機典型的各種運動形式及其復合運動的簡化模型，目的只是在于建立各種離心機運動的基本力學關系，探討各類運動形態下，在力學意義上對試件、受試者及對離心機的影響等概念性問題，以便增強對離心機的整體認識與把握，熟悉離心機各運動關系間相互影響的輕重緩急與主要方面，提供進行離心機概念設計和方案設計時的基本思維與方法。如果讀者對復雜離心機的運動學和動力學感興趣，需要進行詳細計算時，可利用現代設計方法與仿真計算工具再行解決。

離心機大部分的主軸都具有內孔，以供通電、通水、通氣等線纜與管道穿過，結構比較粗壯，具有很好的剛性。因此，包括高加速度土工離心機在內，其最高轉速也遠低于其主軸臨界速度。如果支撐系統也設計良好，轉子系統具有足夠剛性情況下，離心機在作運動分析時可以假定：

· 主軸系統為剛性轉動鉸，可不考慮轉軸撓度及其支撐變形；

· 轉子整體的變形量與其半徑相比甚小，可忽略轉子的變形。

因此，

· 對離心機運動學和動力學進行宏觀基本分析時，可將其簡化為剛體定軸轉動問題；

· 而對離心機結構強度、剛度等進行微觀分析時，則應按實際結構進行之。

6.1 單軸轉動離心機

圍繞主軸進行勻速或勻加速旋轉的單軸轉動狀態是離心機最基本的運動狀態，適用于固定吊籃物體離心機和忽略吊籃甩動過程的土工離心機，以及掛有無動力源自然甩動的單軸艙載人離心機，它們估計占有離心機總數的九成以上。

物體離心機包括土工離心機。由于限制啟動的切向加速度，啟動過程比較緩慢，而且吊籃在低加速度條件下很快就接近甩平，因此，這些離心機在概念設計階段，連勻加速運動都毋庸考慮，只需為啟動留有適當驅動余量，直接考察其極限狀態即最高穩態運動狀態即可。

只有載人離心機和動態飛行模擬器，由于其最大法向加速度和切向加速度數值比較接近，都在10g左右這樣一個低數量級，試驗對象又是十分重要和敏感的“人體”，才會考慮座艙甩動和切向加速度等動態因素，甚至還可能計及1g重力加速度，特別是其方向的影響。

總之，對于單軸轉動離心機的研究，可以概括絕大多數離心機，也是研究一切離心機的基礎。它可以利用理論力學剛體定軸轉動的所有分析方法，其原理并不復雜。

6.1.1 單軸離心機運動學

作為離心機設計基礎—單軸轉動離心機，可采用標量法進行計算，見圖6-1。

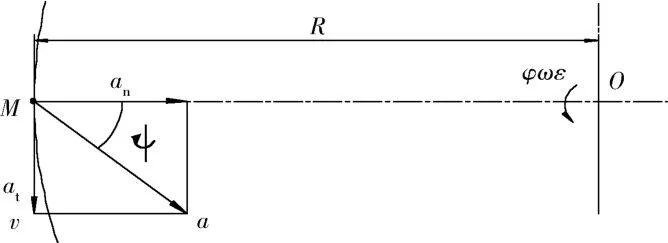
圖6 -1 典型的單軸轉動離心機之運動Fig.6-1 A typical single-axis rotating centrifuge

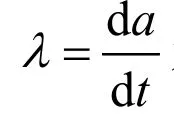
根據圖6-1所示，O為離心機主軸，對離心機轉子上任意點M，可建立單軸離心機運動方程（或稱為主軸運動方程）如下：

對式(6-1)連續求導，可逐步得到主軸轉動角速度ω（rad/s）和主軸轉動角加速度ε（rad/s2）為

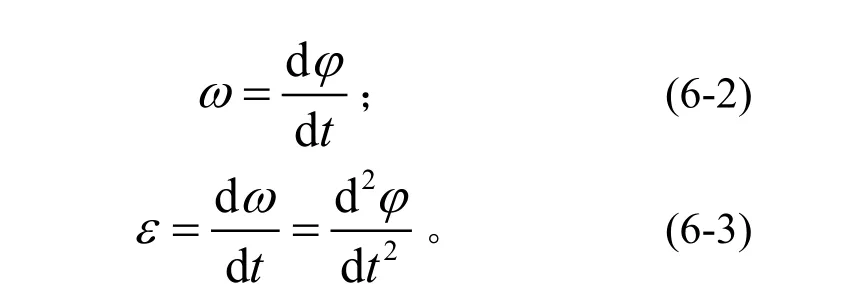
或另表達為

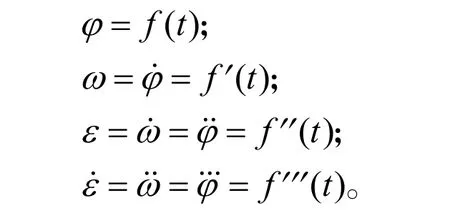
當ε為常數，即勻加速轉動情況下，分別設φ0、ω0為t=0時的初始轉角和角速度，由理論力學得

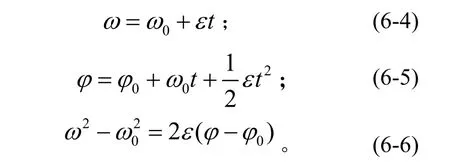
工程計算中通常以每分鐘轉數n（r/min）表示角速度時，它與ω（rad/s）的關系為

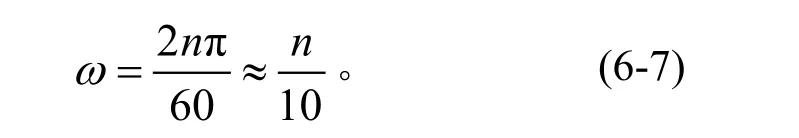
轉子的角速度也就是它的轉動圓頻率或角頻率。而轉子運動周期T（s）則為

轉子轉動頻率f（Hz）為

M點的轉動線速度ν（m/s）為：

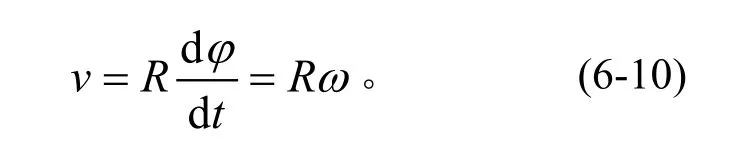
對上式求導，可得M點切向加速度（反映速度大小的變化快慢）為

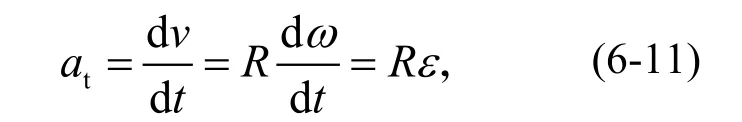
式中at的單位為m/s2。

轉換公式后，得到ε（rad/s2）為

M點法向加速度（反映速度方向的變化快慢）為

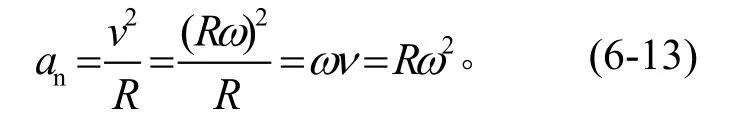
式中an的單位為m/s2。

公式(6-13)經轉換后，得到ω（rad/s）為

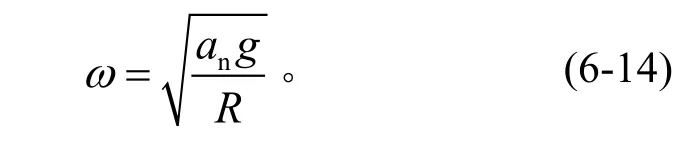
M點合成加速度為

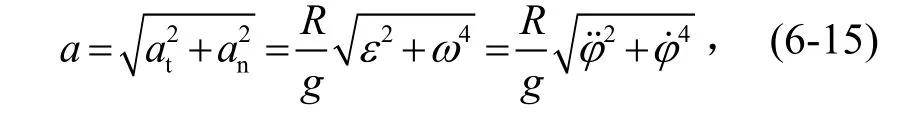
合成加速度a與半徑OM的夾角ψ之正切為

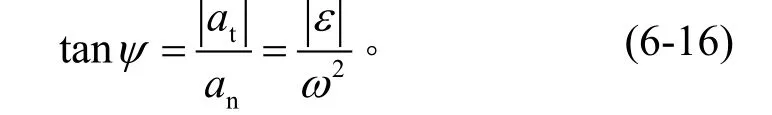
在三維狀態下，當離心機的合成加速度計入重力加速度時（參見圖6-2），變為下式：

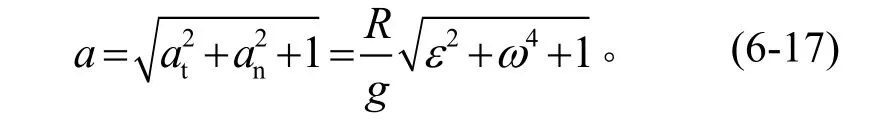
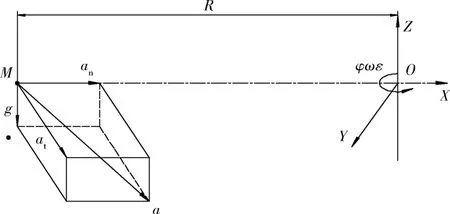
圖6 -2 單軸離心機計入重力加速度的合成加速度Fig.6-2 The composite acceleration including the gravity acceleration of a single axle centrifuge

作為載人離心機和動態飛行模擬器，精確計算時可按公式(6-17)進行；對于物體離心機和土工離心機，一般按公式(6-13)或公式(6-15)直接計算向心加速度或合成加速度即可。

工程上，當已知離心機每分鐘轉數為n（r/min）時，法向加速度式(6-13)可轉換為

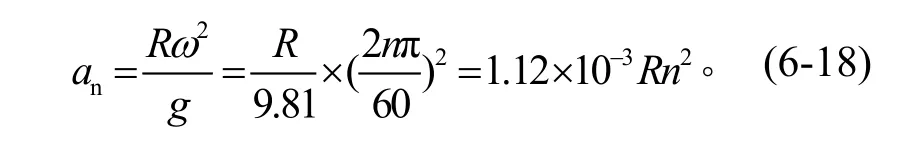
關于各運動參數的方向，統一說明如下：

1）圖6-2表示一系列正向和加速狀態的關系：即轉軸z軸向上為正，從上往下看當φ、ω、ε逆時針方向時為正（按右手規則，拇指指正向，四指自然彎曲方向為正），相應at、a、v也是正向。

2）而法向加速度an永遠指向轉軸中心，稱之為向心加速度。

3）轉動線速度永遠與主軸角速度同向。當角加速度與角速度同向時，切向加速度與線速度同向，轉子加速；反之減速。

6.1.2 單軸離心機動力學

相對于質點動力學基本方程，單軸離心機的質點動力學方程可表達為

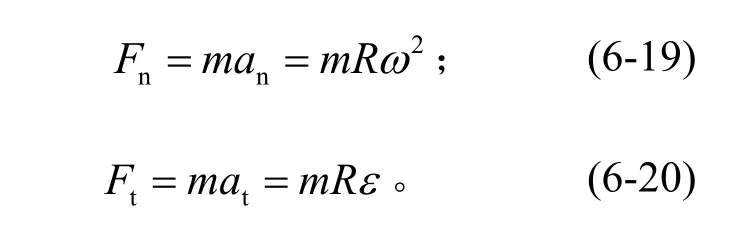
在式(6-19)和式(6-20)中：Fn為法向力或離心力，N；Ft為切向力，N；m為質量，kg。

對于單軸離心機，重點是關注其法向加速度的動力學問題，它乃離心機最主要的應用價值所在。其一般物理概念為：安裝于離心機上質量為 1 kg的物體，當物體旋轉到法向加速度100g時，所引起的離心慣性力將使其質量力擴大100倍，相當于將1g重力場內的物體放置在100g慣性力場內，其“重量”增加了100倍一樣，量綱換算如下：

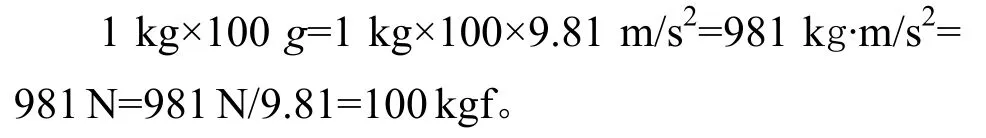
相對于定軸轉動動力學，當不計風阻時，可得到單軸離心機的轉動微分方程為

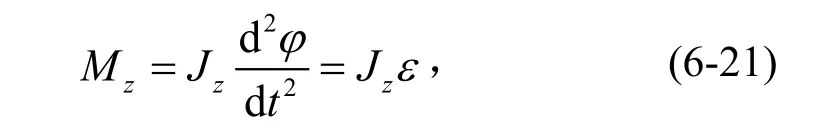
式中：Mz為對z軸（主軸）的力矩，N·m；Jz為對z軸（主軸）的轉動慣量，kg·m2；ε為角加速度，rad/s2。

由此可見，轉軸力矩等于對轉軸的轉動慣量與角加速度的乘積（相當于直線運動時的F=ma），或轉軸力矩與其角加速度成正比。

同樣，我們也可得出以下一些主要表達式。

離心機轉子的動能為式中T為轉子動能，J 。

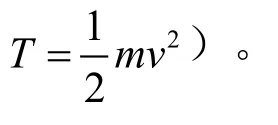
常用量綱換算為 1 J=1 N·m=1 kg·m2/s2。

離心機的轉動功率為：

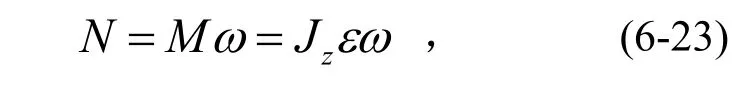
式中N的單位為W。

可見：離心機轉動功率等于其力矩與角速度的乘積（相當于直線運動時P=Fv），或表示為：轉動功率與角速度和角加速度的乘積成正比。

常用量綱換算為

1 W= 1 J/s=1 N·m/s=1 kg·m2/s3。當計入離心機風阻時，且已知無限空間內典型的迎風阻力為

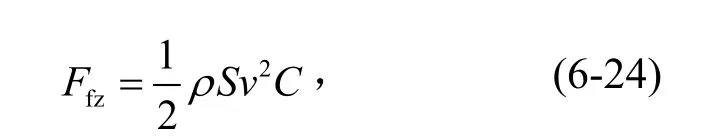
式中：Ffz為風阻，N；C為轉動體正面空氣阻力系數；ρ為空氣密度，ρ=1.185 kg/m3；S為轉動體迎風面積，m2；v為轉動體運動速度，m/s。

由式(6-24)可得到由于風阻產生的力矩為

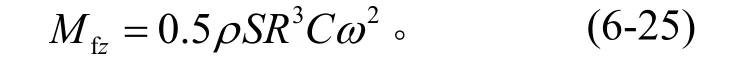
因此，當計入風阻時的單軸離心機，其轉動微分方程式變為

實際上，離心機處于有限空間內，如果計入氣團速度，氣動阻力將會減小，詳細計算與分析可見第7章。

6.2 雙軸轉動離心機

所謂雙軸轉動離心機即除離心機主軸外，轉臂端部增加了一根懸掛吊籃或座艙的轉動軸，使吊籃或座艙隨著離心機轉動，靠著離心力可以自由甩動的離心機，主要指帶擺動吊籃的土工離心機和單軸艙載人離心機。

雙軸離心機穩態運行時的運動學分析與單軸離心機基本相同，只不過將旋轉半徑理解為包含吊籃或座艙甩動半徑在內而已；雙軸離心機動態過程主要發生在啟、制動和模擬隨機曲線的過程中，其中啟動過程更為嚴酷，下面將以啟動過程為例加以說明。

作為穩態加速度模擬試驗設備——離心機的正常運轉，當然應該以“穩”為主，因此在物體離心機和土工離心機相關試驗標準中，特意規定了切向加速度的限制要求；而載人離心機恰恰相反，需要其快速啟、制動以便可以進行機動飛行時的動態模擬，因此，離心機的動態分析主要針對的就是載人離心機。

單軸離心機原理簡單，但雙軸離心機及多軸離心機的運動分析將越來越復雜，會涉及非線性或高次高階微分方程，有的方程不一定有解析解或簡單解，就是有解也不易說明問題。為此，本節將采用MATLAB軟件來圖解方程或采用簡算方法進行分析說明，盡量形象明確地（雖不是精確地）進行闡述。

6.2.1 雙軸離心機運動學

雙軸離心機運動學的分析，除與單軸離心機具有共同之處外，即主軸運動學分析外，只需補充座艙的甩動與離心機主軸間的運動關系即可。

本節分析雖然也適用于具有擺動吊籃的土工離心機，但土工離心機并不需要研究吊籃甩動過程，因此，研究重點從此已經轉向載人離心機。所以，按照相應習慣，將采用重力“G”代替重力加速度“g”來表述“超重”概念。

雙軸載人離心機實際上就是指單軸艙載人離心機；三軸載人離心機也就是雙軸艙載人離心機。

圖6-3為單軸艙載人離心機的甩動過程示意圖。

圖6 -3 單軸艙載人離心機自由甩動過程分析Fig.6-3 Analysis of single-axis cabin free swinging

為了有效利用離心力實現自主甩動，座艙總質心M與其擺動軸O-O'間必須有適當的偏置量r；靜止狀態下，座艙必然會自然下垂，甩動半徑與鉛垂線夾角θ=0°；這時，離心機原始轉動半徑R0剛好等于轉臂的有效長度R'；當座艙甩起后，離心機轉動半徑逐漸在變長，其變化范圍為：R=R'+rsinθ。

設主軸角速度和角加速度分別為ω和ε，座艙甩動角速度為ωg，根據受試者通常的原始座位，可稱之為滾轉角速度，質心M點的法向慣性加速度為anI，與重力加速度g的合成加速度為a。

從圖中，可建立起座艙甩動的運動方程如下：

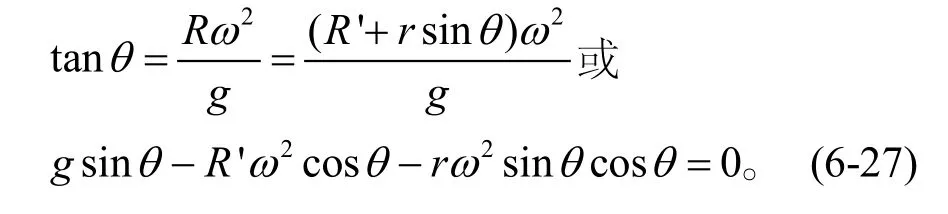
對這個非線性方程求解，不如采用舉例觀察圖形來得直觀。

設某離心機轉臂有效長度為R'=7.5 m，座艙質心偏置量r=0.5 m，利用MATLAB軟件可將式(6-27)繪成如下關系圖（見圖6-4）。

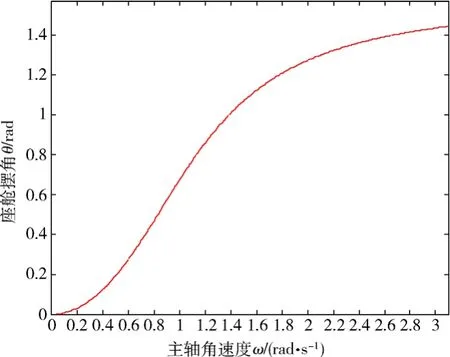
圖6 -4 單軸艙載人離心機座艙擺角與主軸角速度關系Fig.6-4 Relationship between cabin tilt angle and main axle angular speed for single axle cabin centrifuge

討論：

1）單軸艙載人離心機的座艙擺角與主軸角速度密切相關。

2）由圖 6-4可見座艙擺動的規律：當離心機從靜止開始啟動時，一開始，座艙甩動得比較緩慢；之后，擺角則依直線增長；至某角速度以后，增長漸趨緩和，表明座艙已接近水平。因此，呈兩頭慢中間快的特點。

3）單軸艙載人離心機從靜止或某一初始狀態快速啟動時，毋需 1 s，座艙就可基本甩平。在此期間，離心機旋轉半徑是變量，對于本例來說，半徑最大變化率僅為0.5/7.5= 6.67%，意味著對徑向加速度的影響也只不過是如此的比例。

4）單軸艙載人離心機受限于結構關系，座艙甩動過程中，徑向加速度只與重力加速度進行合成，而數值數倍于重力加速度的切向加速度卻無法參與進來；因此，加速度在數值的合成上，就已經包含了更大的誤差，以后討論會知道，其影響遠遠超過半徑變化所引起的法向加速度誤差。并且，切向加速度除數值較大以外，更重要的是方向性誤差對受試者影響更為重要，而半徑變化僅僅影響的只是法向加速度的些許量值而已。

5）因此，綜合對受試者影響程度而言，筆者認為：一般情況下，單軸艙載人離心機進行運動學分析時，完全可以忽略半徑變化這一因素，即可忽略座艙甩動過程對徑向加速度的影響。

6.2.2 雙軸離心機動態過程

預先說明：

1）動態過程的研究重點將放在啟動過程，放在對啟動加速度變化率與主軸運動參數間的關系分析上；

2）以下分析中，將忽略啟動過程的半徑變化量；

3）舉例說明時，一律以半徑R=8 m、g=9.81 m/s2、啟動率為λ=6G/s的相應離心機為例。

6.2.2.1 雙軸載人離心機的啟動

設單軸艙載人離心機以加速度變化率λ啟動。其初始合成加速度為a0、合成加速度a與加速度變化率λ的關系可表示為[1]

對于單軸艙載人離心機，限于結構原因無法計入其切向加速度，而合成加速度主要是由法向加速度和重力加速度二者所構成：

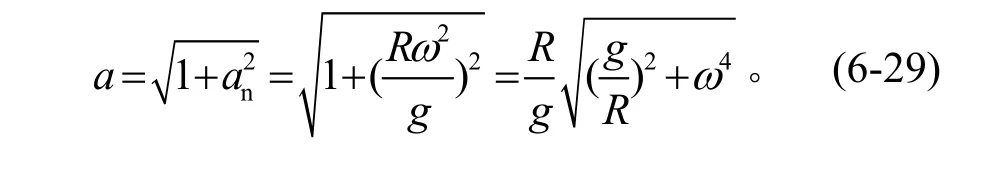
比較式(6-29)和式(6-28)，得到

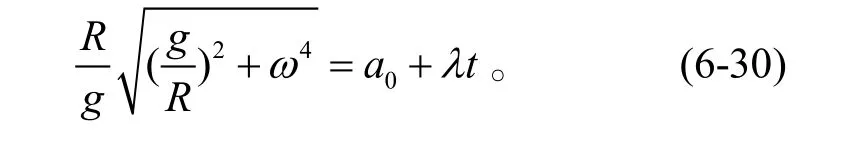
根據該式，當計入重力加速度時：

·初始合成加速度沒有等于零的情況；

·當t=0，an=0，ω0=0時，初始合成加速度a0=1G，即等于重力加速度；當以λ=6G/s啟動后，t=1 s時，合成加速度a=7G；

·當t=0，an=1G，ω0=ω0時，初始合成加速度a0=1.414 2G；當以λ=6G/s啟動后，t=1s時，合成加速度a=7.414 2G；

·也就是說，這種情況下合成加速度始終以一個g為基礎、為背景。

以下再通過舉例進行具體分析。對于固定半徑為8 m的單軸艙載人離心機，其合成加速度與主軸角速度的關系如圖6-5所示。

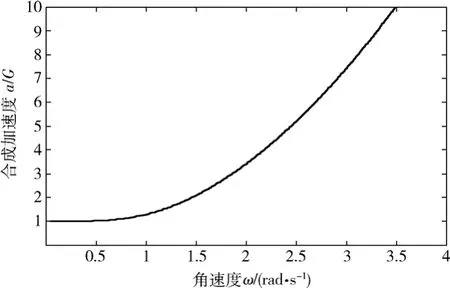
圖6 -5 單軸艙載人離心機合成加速度與主軸角速度關系Fig.6-5 Single-axle cabin human centrifuge resultant acceleration versus main shaft angular speed

由圖可見，隨著主軸角速度增加，合成加速度以圖示曲線增加，角速度為零時，合成加速度為1G。

對式(6-29)求導，得啟動率表達式為

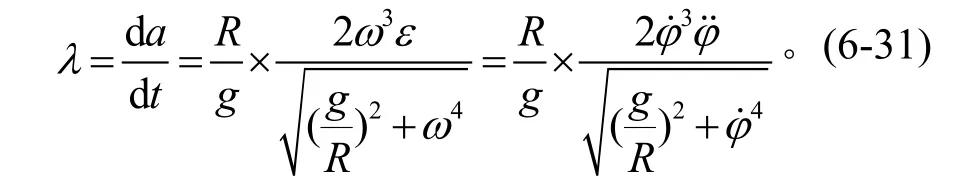
式(6-31)是一個高次二階微分方程式。利用它求半徑 8m單軸艙載人離心機從靜止開始的啟動過程中，啟動率分別為λ=1～6G/s時，主軸角速度與角加速度的關系如圖6-6所示。

圖6 -6 單軸艙載人離心機由靜止啟動時的主軸角速度與角加速度關系Fig.6-6 Relationship between angular velocity and angular acceleration of main axle for single-axle cabin human centrifuge startup

圖6-6表明：當角速度較低時，角加速度呈開放狀態。討論：

1）單軸艙載人離心機由靜止啟動瞬間，當角速度為零時，需要非常大的角加速度，就是說，需要很大的驅動力矩來推動轉子；

2）不論啟動率大小，其規律基本一致；

3）說明，當單軸艙載人離心機以任一啟動率啟動情況下，一開始必然伴隨著超大力矩需求，處理不當，引起沖擊是完全有可能的；

4）啟動后，角速度突然出現階躍值；角速度一旦出現，角加速度迅即減小，之后呈緩慢增長趨勢；

5）這就是關于載人離心機啟動過程，需要建立的第一個必不可少的力學概念，即由靜止直接啟動離心機，需要非常大的驅動力矩。

既然如此，人們就想到從徑向加速度1G啟動的方法。此時，與重力加速度的合成加速度等于1.41G，按固定半徑8 m計算時，其初始角速度為

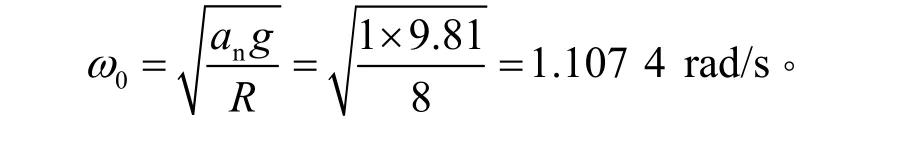
圖6-7表示的就是從1.41G啟動的情況，即以ω0=1.107 4 rad/s啟動。可見：

1）啟動瞬間，角加速度已出現有限值，表明啟動過程所需力矩大為減小，沖擊緩和；

2）隨著啟動率變小，沖擊愈趨減小；

3）角速度由零逐漸增加；

4）其余情況與前基本相同。

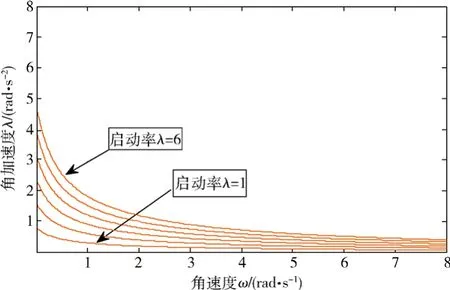
圖6 -7 單軸艙載人離心機由1.41 G啟動時的主軸角速度與角加速度關系Fig.6-7 Relationship between angular velocity and angular acceleration of main axle for single-axle cabin human centrifuge starting from 1.41 G

將式(6-31)轉化為下式：

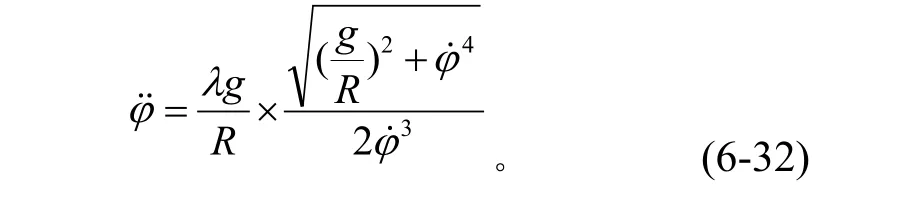
式(6-32)通過MATLAB數值求解，可得到單軸艙載人離心機從靜止以λ=6G/s啟動時的角位移與角速度的變化情況（參見圖6-8）。

圖6-8表明：在時刻為零、靜止狀態時，角速度已有一個跳躍。如前所述，即需要大的角加速度介入。

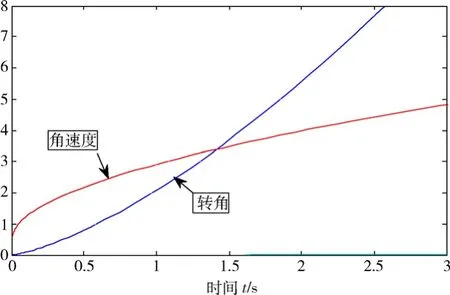
圖6 -8 單軸艙載人離心機由靜止啟動的轉角與角速度Fig.6-8 Single axle cabin human centrifuge’s rotational angle and angular velocity startup from rest

該曲線啟動1 s附近時的具體數據如表6-1所示。

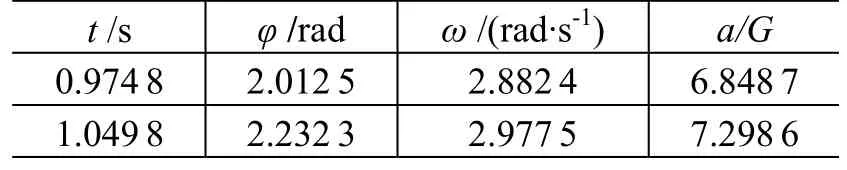
表6 -1 單軸離心機從靜止啟動1 s左右的數據Table 6-1 Single axle cabin human centrifuge’s start data about one second startup from the static

可見，1 s時的合成加速度當為7G。圖6-9表示了由1.41G與由靜止狀態，均以λ=6G/s啟動時的比較圖。

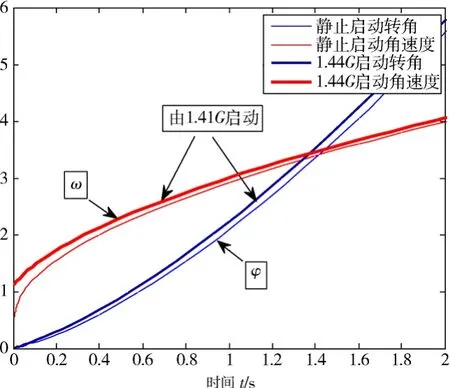
圖6 -9 單軸艙載人離心機由靜止和1.41 G啟動比較Fig.6-9 Single axle cabin human centrifuge startup from rest and from 1.41 G

啟動1 s左右時的數據如表6-2所示：

表6 -2 單軸離心機從靜止啟動1.41 G左右的數據Table 6-2 Single axle cabin human centrifuge’s start data about one second startup from 1.41 G

可見，1 s時的合成加速度約為7.41G。

討論：

1）由1.41G啟動，其初始角速度基本上已相當于靜止啟動時的平穩增長段，躲過了超高角加速度出現的極端情況，所需角加速度大為減少；

2）由1.41G啟動，除啟動瞬間角加速度有一點沖擊之外，其余曲線段都比較平穩；

3）由1.41G啟動，可消除機械傳動系統的齒隙和靜、動態摩擦狀態轉換時的非線性過程；

4）因此，從1.41G啟動，無疑是載人離心機最好的啟動方式。

（未完待續）

（Reference）

[1]Drone K C.Design study for an acceleration research device, AD 268621[R], 1961