離心葉輪軸面液流過水斷面面積解析

馬銀珍

(山西省水利水電勘測設計研究院,太原030024)

軸面液流過水斷面是離心葉輪葉片水力設計中的重要概念,這一斷面指葉輪內一個與所有流面正交的回轉曲面。該斷面上各點處的流體質點的絕對速度都與斷面斜交,但絕對速度的軸面分量將與斷面垂直。這一斷面面積的計算在葉輪設計中有著重要的作用。比如,在計算葉片進口邊某點的葉片安放角時,就必須計算通過葉片軸面圖上給定點的軸面液流過水斷面面積;葉輪軸面投影圖的繪形質量也要通過考察這一斷面面積隨流道中線的變化規律來保證。

盡管軸面液流過水斷面面積與葉片設計精度和質量關系密切,但是長期以來,在傳統的設計方法中,都只能計算這一面積的近似值[1-2]。筆者將以線積分和重心定理為基礎,通過數學分析方法,給出了這一面積的精確解,以供設計人員參考,并可作為設計高水平的葉輪繪圖軟件的重要依據。

1 數學背景

如圖1所示,xoy平面上有一平面曲線AB,其長度為l。這一平面曲線繞y軸旋轉一周生成一回轉面,這一回轉面的面積a可以計算求解如下。

在曲線上取一點,其坐標為(x,y),曲線上包括這一點的一微弧段長d l,如果曲線的線密度為l,這一微弧段對y軸的力矩為x d l,由此,全曲線對y軸的力矩M為：

如果平面曲線的重心C到y軸的垂直距離為xc,由重心定義,全曲線對y軸的力矩M也可表示為

圖1 曲線重心

比較(1)、(2)式,可以得到

另一方面,微弧段d l繞y軸旋轉一周生成的微回轉體可視為一高等于d l,半徑為 x的圓柱面,其表面積d a=2πx d l,全曲線繞y軸旋轉一周生成的回轉面面積a,可積分上式得到

由此得到結論：一平面曲線繞平面上任一直線旋轉一周生成的回轉面面積,等于2π倍曲線長和曲線重心到給定直線的垂直距離的乘積。上述結論稱古魯金定理。但應注意,平面曲線的重心不一定位于曲線上。

2 軸面液流過水斷面面積計算的傳統方法

如圖2所示,在初定或最終確定的葉輪軸面投影圖中作一內切圓O,這一圓與前后蓋板流線相切于A、B兩點。連接OA、OB及AB得到一等腰三角形,存在唯一一條與半徑OA、OB相切于 A、B的圓弧。由于OA、OB與前后蓋板流線正交,且圓弧與兩半徑相切,這一圓弧顯然與前后蓋板流線正交。前后蓋板流線是兩條軸面流線。同時認為,上述圓弧與軸面內其他軸面流線也正交。這一平面圓弧繞葉輪軸心線旋轉一周所得到的回轉面就是一軸面液流過水斷面,這一斷面顯然符合過水斷面的定義。

圖2 尋求曲線重心的傳統方法

在傳統的葉輪設計過程中,當獲取了上述弧長之后,用下述方法確定圓弧重心的位置：將等腰三角形底邊上的高三等分,把靠近三角形底邊的一個分點C視為圓弧重心,量出這一點到葉輪軸心線距離后,即可由上面導出的古魯金定理計算這一過水斷面面積。

3 軸面液流過水斷面面積計算的新方法

為利用古魯金定理計算軸面液流過水斷面面積的精確值,由式(5)可知,必須尋求軸面上作為軸面液流過水斷面形成線的圓弧的長度,及其重心的正確位置。

傳統方法中確定的重心實質是等腰三角形的重心,將三角形的重心作為圓弧重心顯然是一種近似。下面首先將導出重心位置的精確解。

如圖3所示,將直角坐標原點置于圓弧的圓心M,x軸等分圓弧且與圓弧對應的弦AB垂直。設弧半徑為R。在弧上取一點K,通過K點的圓弧半徑與x軸正向夾角為θ,弧上一微弧段長d s且通過K 點。如果d s對應的圓心角為 dθ,那么 d s=R dθ。設單位長度弧長重l單位,這一微弧段對y軸的力矩應為R cosθd s=R2cosθdθ,全弧對 y 軸的力矩顯然為

另一方面,全弧對y軸的力矩應為全弧長s乘以弧重心到y軸的距離x,由此有方程

弧重心顯然位于弧對稱軸即 x軸上。求出了圓弧重心到y軸距離x后,就可以在x軸上標出重心位置。式(6)中未知量圓弧半徑R和圓弧長s的求解將在下面說明。s值不僅關系到式(6)中 x值,在最后應用古魯金定理時也要用到。

在設計實踐中,本文給出的軸面液流過水斷面面積的求解過程如下：

1)在葉輪軸面投影圖上作一與前后流線都相切的內切圓,并作出等腰三角形OAB,如圖3所示。

2)用繪圖軟件量出三角形的腰長(OA或OB)l,同時量出三角形的頂角∠AOB值Φ。在葉輪軸面平面上,量取這兩個幾何量都很容易。

3)按本方法中不必實際作出圓弧。根據測量所得的l和Φ值,可以得到圓弧所在園半徑R=l?tan(Φ/2),這是因為△MAO及△MBO均為直角三角形。

圖3 尋求曲線重心的新方法

圓弧長s比較易于計算。圓弧所在圓的周長為2πR=2πl tan(Φ/2),由于 ∠AMB=π-Φ(括號內的Φ值單位應為弧度,下同),于是弧長

s=2πl tan(Φ/2)?(π-Φ)/2π=

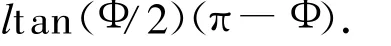
s也可用繪圖軟件直接精確量取。考慮到∠AMO=∠AMB/2=(π-φ)/2,以及 R=l tg(φ/2),由式(6),圓弧重心到M距離x應等于

4)由直角三角形MAO可求出OM長為l/cos(Φ/2),這也是等腰三角形頂點到y軸的距離,那么圓弧重心到等腰三角形頂點距離顯然為

5)在等腰三角形的高上取一點,使這點到等腰三角形頂點距離為上述值,由此就精確地確定了圓弧重心在葉輪軸面圖上的位置。用繪圖軟件量出這點到葉輪軸心線的距離,并乘上2π倍已獲取的s,由前面導出的古魯金定理即可得到平面圓弧(軸面液流過水斷面形成線)繞葉輪軸心線旋轉一周所得軸面液流過水斷面面積。

4 結束語

在離心泵葉輪設計實踐中,準確計算葉輪內軸面液流過水斷面面積是提高設計質量的重要措施。筆者以數學分析和重心定理為依據,導出了這一值的解析求解方法。這一方法將成為水泵設計工程師完成優質設計的新工具。

致謝：本文在寫作中得到西華大學能環學院嚴敬教授的指導和幫助,作者在此表示誠摯的謝意!

[1] 嚴敬.低比轉速離心泵[M].成都：四川科學技術出版社,1998：144-147.

[2] 關醒凡.現代泵技術手冊[M].北京：宇航出版社,1995：203-204.

[3] 哈爾濱工業大學理論力學教研組.理論力學[M].5版.北京：高等教育出版社,2007：176-187.

[4] 同濟大學應用數學系.高等數學[M].5版.北京：高等教育出版社,2002：264-288.

[5] 戴正元,谷傳剛.離心泵葉輪軸面流道計算新方法[J].工程熱物理學報,2003,24(5)：783-785.

[6] 劉棟,楊敏官,王群,等.離心泵內部流場實驗研究與數值計算[J].中國農村水利水電,2008(9)：87-91.