耐熱合金蜂窩等效熱導率的實驗研究①

趙 劍，謝宗蕻，李 瑋，田 江

(西北工業大學航天學院，西安 710072)

0 引言

蜂窩夾芯結構是一種先進的輕質結構型式，其通常由上、下2層薄蒙皮和中間的蜂窩芯體組合而成，具有比強度、比剛度高，隔熱、隔振性能好等優點，在火箭整流罩、飛機機身、航空發動機短艙、現代衛星等航空航天結構件中得到廣泛應用。鑒于上述優點，耐熱合金蜂窩夾芯結構也成為高超音速飛行器和新一代可重復使用運載器熱防護系統面板的理想方案[1－2]。耐熱合金蜂窩夾芯結構用作熱防護系統面板，進行設計時必然涉及傳熱分析。由于蜂窩芯體的幾何不連續性，導致其內部傳熱模式相當復雜，包括金屬胞壁的固體導熱、蜂窩腔體內的氣體導熱，以及蜂窩上下面板間的輻射換熱等幾種不同模式。熱分析時，如果對蜂窩芯體和其內部的傳熱模式進行詳細建模將使分析模型過于復雜，通常期望將蜂窩芯體等效為連續的實體，采用蜂窩芯體的宏觀等效熱導率進行傳熱分析。

關于蜂窩夾芯結構傳熱分析方面的研究多采用細觀方法，分析蜂窩結構的傳熱性能[3－7]，而通過實驗方法獲得蜂窩等效熱導率的研究尚比較缺乏[7－8]。文獻[9－10]進行了金屬蜂窩的傳熱實驗研究，其中文獻[9]分析了鎳基合金蜂窩板在高溫下的防熱特性，但并未討論鎳基合金蜂窩的等效熱導率;文獻[10]對鋁蜂窩平板進行了模擬氣動加熱實驗，測定了加熱表面和非加熱表面的瞬態溫度，同樣未給出金屬蜂窩的等效熱導率。

本文針對可在高溫環境下工作的Hastelloy X合金蜂窩夾芯結構進行穩態傳熱實驗研究，獲取其在不同溫度下的等效熱導率，并采用Swann-Pittman半經驗模型計算其等效熱導率。

1 實驗

1.1 實驗原理

采用穩態方法測量蜂窩夾芯結構試件的宏觀熱導率。如圖1所示，將試件置于加熱板上，試件外表面裸露在空氣中，通過輻射和對流方式向外界散熱。實驗中采用氧化鋯絕熱材料密封試件四周，使絕熱材料高度與試件平齊，以阻止熱量沿側向傳遞。當系統達到熱平衡時，可近似視為一維穩態導熱情況。

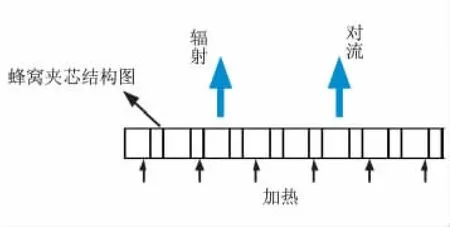
圖1 試件傳熱示意圖Fig.1 Sketch of heat transfer modes at the specimen

由傅里葉定律，沿試件厚度方向傳遞的熱流為

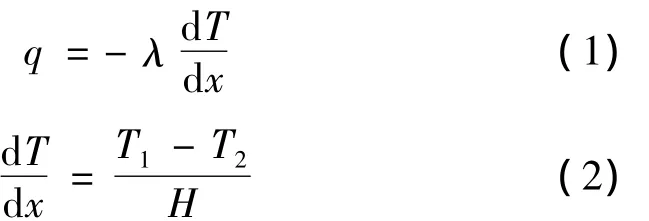
式中q為達到穩態時沿試件厚度方向的熱流密度;λ為試件的等效熱導率;H為試件厚度;T1、T2為達到穩態后試件上下表面的溫度。

系統達到穩態時，試件外表面向環境傳遞的熱量等于從下表面進入試件的熱量。

試件上表面以熱輻射和熱對流形式向環境傳遞熱量。其中，輻射熱流由Stefan-Boltzmann定律得

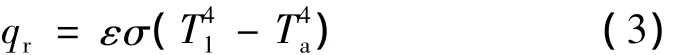
式中 ε為試件外表面的發射率;σ為Stefan-Boltzmann常數，σ =5.67 ×10－8W/(m2·K4);Ta為環境溫度。

試件上表面與空氣間的對流換熱可視作大空間自然對流換熱情況[11]。工程上廣泛采用如下的實驗關聯式計算大空間的自然對流換熱:

其中:

式中Nu為Nusselt數;Gr為Grashof數，在自然對流現象中，其作用相當于強制對流中的Reynolds數;Pr為Prandtl數;C為常數;α為體積膨脹系數;Δt為壁溫與環境之間的溫差;ν為流體在定性溫度下的運動粘性系數;l為定性長度;g為重力加速度。

恒壁溫下，熱板上表面平均Nusselt數推薦實驗關聯式為

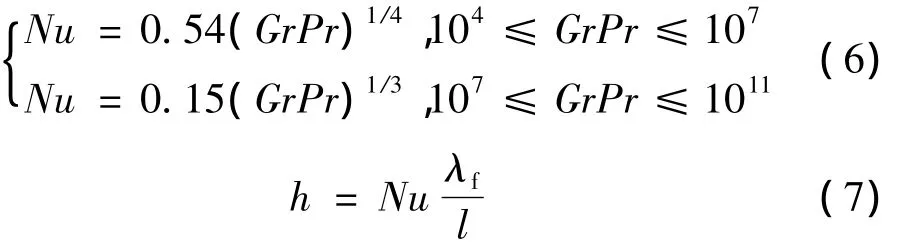
式中l為定性長度;λf為流體在定性溫度下的熱導率;h為對流傳熱中的表面傳熱系數。

對于恒壁溫條件下熱面朝上的平板自然對流問題，定性長度為平板的表面積與周長之比，定性溫度取邊界層膜溫度:

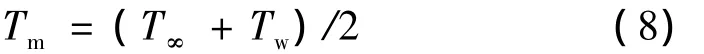
由牛頓冷卻公式，對流換熱熱流為

將式(3)和式(9)疊加，得到試件上表面向外散熱的總熱流qo，則試件的等效熱導率為

由式(10)得到的是耐熱合金蜂窩夾芯結構試件的等效熱導率，其中耐熱合金蜂窩芯體的等效熱導率可采用熱阻分析方法得到。

蜂窩夾芯結構的總熱阻為

蜂窩夾芯結構中的上面板、蜂窩芯體和下面板屬于串聯導熱情況，總熱阻等于各串聯熱阻之和:

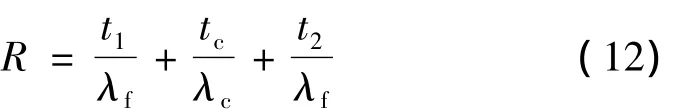
式中t1、t2、tc分別為上、下面板、蜂窩芯體的厚度;λf為面板材料的熱導率;λc為蜂窩芯體的等效熱導率。

聯合式(11)、式(12)可求得 λc。

1.2 實驗系統與試件

實驗系統由大功率高溫加熱器、可控硅控制器、PSI多通道溫度掃描閥、數據采集計算機等組成，如圖2所示。測溫傳感器采用k型快速反應熱電偶。

蜂窩夾芯結構試件由耐熱合金材料Hastelloy X制成，Hastelloy X合金是一種添加了鈷和鎢的鎳-鉻-鉬合金，具有較好的高溫強度，可在900℃以下長期使用。

試件的幾何尺寸如表1所示，Hastelloy X合金材料的熱導率如表2所示。如圖3所示，在試件的裸露表面靠近中心的部分均勻布置5支熱電偶，通過求其平均值來代表試件上的表面溫度。本研究制作了表面情況與待測蜂窩夾芯結構外表面相同的標準試件，采用比較法測量其表面發射率為0.54。

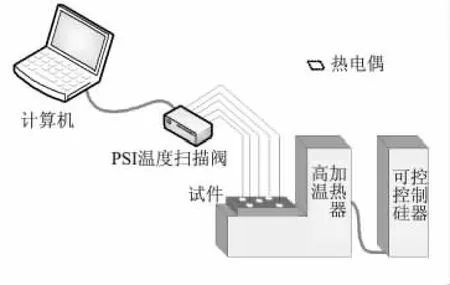
圖2 實驗系統示意圖Fig.2 Sketch of the test system

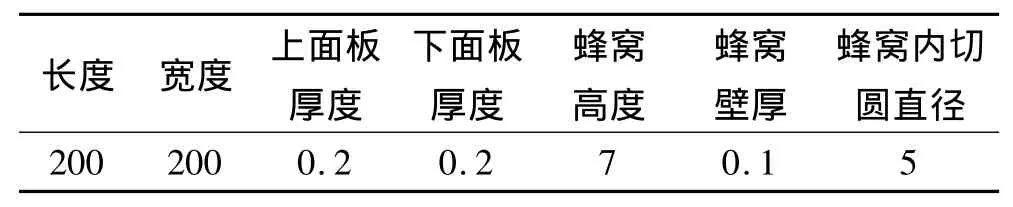
表1 耐熱合金蜂窩夾芯結構試件幾何尺寸Table 1 Geometries of the refractory alloy honeycomb sandw ich specimen mm

表2 Hastelloy X合金熱導率Tab le 2 Thermal conductivities of Hastelloy X alloy

圖3 試件實物照片Fig.3 Photo of the specimen

2 理論預測模型

耐熱合金蜂窩夾芯結構受熱時，蜂窩內部存在的傳熱模式主要包括金屬胞壁材料的固體導熱，蜂窩腔體內的氣體導熱，以及蜂窩腔內面板間的輻射換熱等。Swann與Pittman假定蜂窩夾芯結構的面板厚度足夠小，采用有限差分法分析蜂窩結構的輻射和導熱復合傳熱問題，提出了蜂窩結構內輻射換熱經驗公式[7，12]，利用并聯模型得到了蜂窩結構等效導熱半經驗公式:

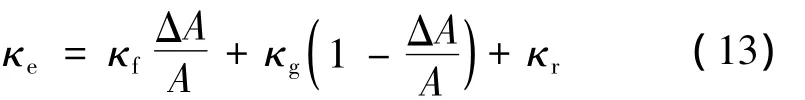
式中 κe為等效熱導率，是蜂窩芯幾何尺寸和材料熱物性參數的函數;κf為蜂窩胞壁材料的熱導率;κg為蜂窩腔內氣體的熱導率;κr為蜂窩芯體輻射換熱等效熱導率;ΔA/A為蜂窩胞壁橫截面積與蜂窩全部面積之比。

氣體熱導率可由式(14)得到:

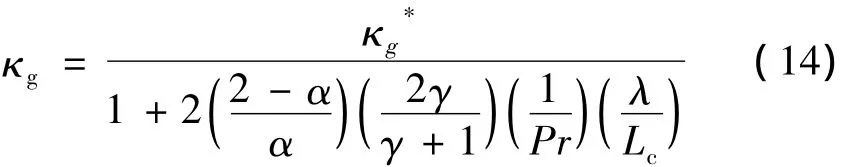
λ值由式(15)決定:

式中KB為波爾茲曼常數;T為溫度;dg為氣體分子碰撞直徑;p為壓力。

式中Tavg為蜂窩板的平均溫度;σ為斯忒潘-波爾茲曼常數ε為蜂窩內部統一輻射率;d為蜂窩單元尺寸。

利用上述半經驗模型預測了文獻[13]中的Inconel 617鎳基高溫合金正方形蜂窩的有效熱導率，并與文中提供的實驗數據進行對比，結果如圖4所示。

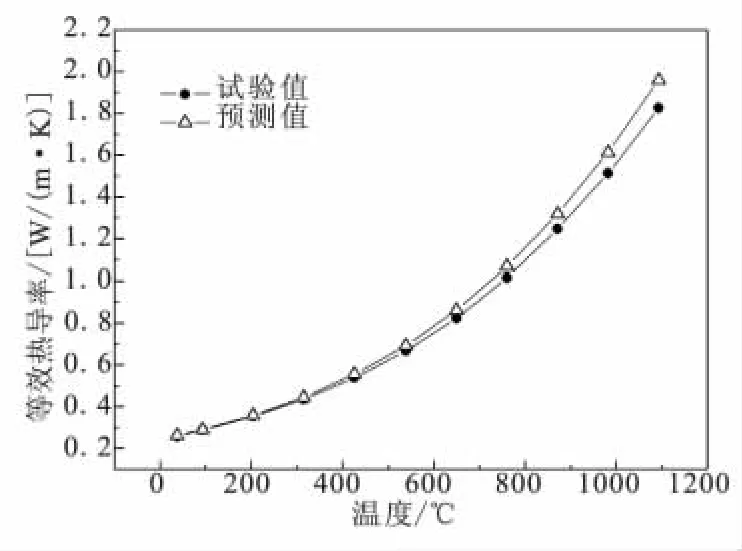
圖4 Inconel 617方型蜂窩等效熱導率實驗值與預測值對比Fig.4 Com parison between tested and p redicted effective thermal conductivities for Inconel 617square honeycomb core

3 結果與分析

圖5為一組系統達到熱平衡后的蜂窩夾芯板熱冷面溫度圖。平衡后冷面溫度較熱面溫度顯著降低，且隨著熱面溫度的升高，熱冷面之間的溫差逐漸增大，在熱面溫度達到630℃時，冷面溫度為549℃，溫差達到81℃。該結果從側面說明耐熱合金蜂窩夾芯結構具有良好的防隔熱效果，且隨著溫度的上升，隔熱效果逐漸增強。

利用Swann-Pittman半經驗模型預測了本研究中采用的Hastelloy X試件的等效熱導率，并與實驗測得的熱導率進行了對比，如圖6所示，兩者吻合良好。對比表2和圖6還可看出，Hastelloy X合金蜂窩的等效熱導率遠小于Hastelloy X合金自身的熱導率，基本小了一個數量級，驗證了蜂窩夾芯結構具有低熱導率特征和良好的隔熱效果。

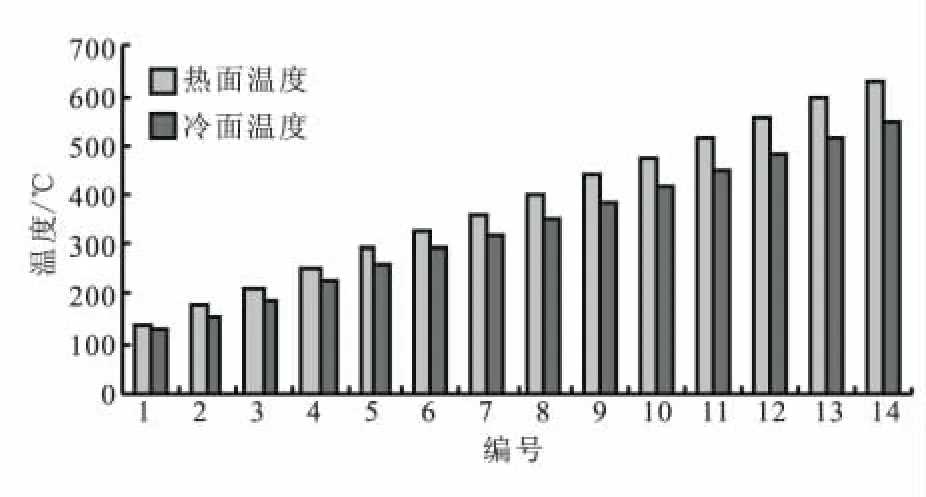
圖5 平衡狀態試件熱冷面溫度Fig.5 Equilibrium tem peratures of the hot and cool sides

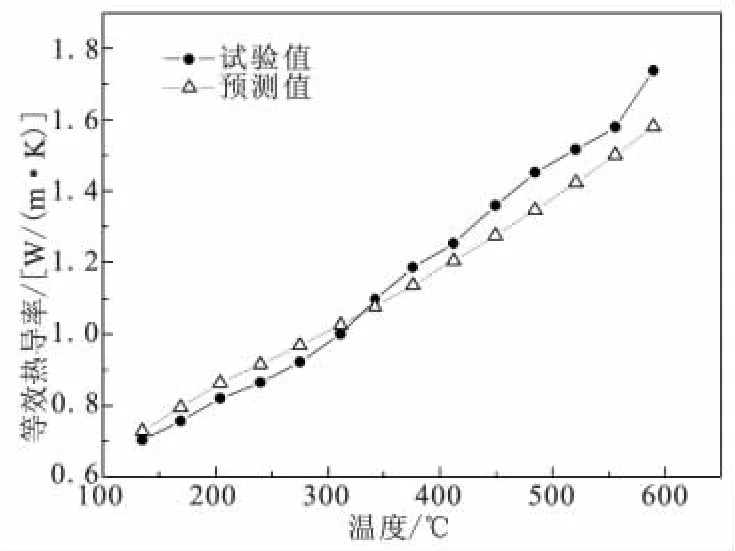
圖6 Hastelloy X六邊形蜂窩等效熱導率實驗值與預測值對比Fig.6 Comparison between tested and predicted effective thermal conductivities for Hastelloy X hexagonal honeycomb core

4 結論

(1)開展了耐熱合金蜂窩夾芯結構穩態傳熱實驗，得到了一組隨溫度變化的蜂窩等效熱導率;采用Swan-Pitmman半經驗模型預測了該蜂窩的等效熱導率，與本實驗結果對比吻合良好，最大相對誤差在10%以內。

(2)溫度越高，耐熱合金蜂窩夾芯結構的隔熱效果越好，耐熱合金蜂窩的等效熱導率比胞壁材料的熱導率小一個數量級。

[1] Max L Blosser.Development of metallic thermal protection systems for the reusable launch vehicle[R].NASA Technical Memorandum 1102996，October 1996.

[2] John T Dorsey，et al.Metallic thermal protection system technology development:concepts，requirements and assessment overview[R].AIAA 2002-0502.

[3] Arulanant ham M，Kaushika N D.Coupled radiative and conductive thermal transfer across transparenthoneycomb insulationmaterials[J].Applied Thermal Engineering，1996，16(3):2092217.

[4] Kamran Daryabeigi.Heat transfer in adhesively bonded honeycomb core panels[R].AIAA 2001-2825.

[5] 唐羽燁，薛明德.蜂窩夾芯板的熱學與力學特性分析[J].航空學報，2005，22(2).

[6] Lu T J.Heat transfer efficiency of metal honeycombs[J].International Journal of Heat and Mass Transfer，1999(42).

[7] Swann R T，Pittman CM.Analysis of effective thermal conductivities of honeycomb-core and corrugated-core sandwich panels[R].NASA TND-714，April，1961.

[8] Stroud CW.Experimental verification of an analytical determination of overall thermal conductivity of honeycomb-core panels[R].NASA Technical Note，TN D-2866，June 1965.

[9] 梁偉，張立春，吳大方，等.金屬蜂窩夾芯板瞬態熱性能的計算與試驗分析[J].航空學報，2009，30(4).

[10] 陳勇，高德平.金屬蜂窩平板加熱過程的數值模擬與試驗研究[J].理化檢驗-物理分冊，2003，39(5).

[11] Bejan Dj M M A，Kraus A D.Heat transfer handbook[M].John Wiley＆Sons，Inc，2003.

[12] Carl CPoteet，Hasan Abu-Khajeel，Su-Yuen Hsu.Preliminary thermalmechanical sizing ofmetallic TPS:process development and sensitivity studies[R].AIAA 2002-0205.

[13] Gorton M P，Shideler J L，et al.Static and aerothermal tests of a superalloy honeycomb prepackaged thermal protection system[R].NASA TP 3257，March 1993.