基于能量法的跨聲速風扇葉片氣彈穩定性研究

趙瑞勇，楊 慧，王延榮

（1.西安航天動力研究所，西安 710100；2.北京航空航天大學能源與動力工程學院，北京 100191）

0 引言

現代葉輪機械正朝著高性能和大容量方向發展，由流體誘發的葉片振動問題也越來越嚴重[1]。其中顫振就是1種典型的流體誘發自激振動[2]。嚴重的葉片顫振可能破壞發動機支撐結構，甚至導致整架飛機失事。因此，在發動機研制過程中，必須避免發動機在整個飛行包線范圍內發生顫振[3]。各類葉片顫振都屬于氣動彈性穩定性問題。氣動彈性試驗破壞性極大，因此，通常應用計算機和CFD技術對氣彈穩定性進行數值仿真研究。葉輪機自身十分復雜，采用直接流固耦合（FSI）計算分析耗時長，很難讓人接受；目前，廣泛采用能量法進行葉輪機械顫振研究，通過計算以轉子振動的某一自然振型表現的顫振與流場之間的能量平衡來預測顫振。計算中通常忽略非定常氣動力對振動模態的影響。因此，該方法實質上是不耦合，或精確地說是弱耦合的，也就不包括非定常氣動力對振型和頻率的反饋影響。基于能量法的簡化方程之所以應用廣泛，主要是因為作用于葉片的非定常氣動力與力矩對金屬葉片的振動模態與頻率影響較小，可以獨立進行結構動力學分析與非定常氣動分析，極大簡化了分析工作。在葉片氣動彈性仿真計算中，由于結構變形，每一計算時間步都需要生成自適應計算網格。采用合理的網格更新方法[6]和尋求高效率、高精度的CSD/CFD數據交換方法是耦合技術應用的關鍵。

本文針對剛性葉片由于變形較小，發展了3維線性插值理論來進行CSD/CFD耦合界面數據交換。

1 葉片結構動力學方程

本文使用有限元法計算葉片的固有振動特性，未考慮葉片間的相互影響，假設每個葉片的振動頻率都相同，模型不計機械阻尼的影響。葉片離心負載下振動的結構動力學控制方程為

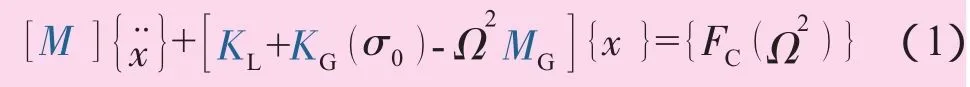
式中：[M]為單元質量矩陣；[KL]為單元彈性剛度矩陣；[KG]為單元離心剛度矩陣；（σ0）為離心力引起的初始應力向量；[MG]為單元離心質量矩陣；{x¨}、{x}分別為單元的加速度向量和位移向量；Ω為葉片的轉動角速度；{FC（Ω2）}為單元節點平衡力向量，此處為離心分布的離散形式。

使用通用軟件ANSYS來計算式（1）。在結構分析中，葉片固連在輪轂上，在葉根處為零線位移和零角位移約束，葉片其它位置為自由約束。給出葉片的各階振型和固有頻率，流場中葉片按照第i階振型和固有頻率進行諧振動

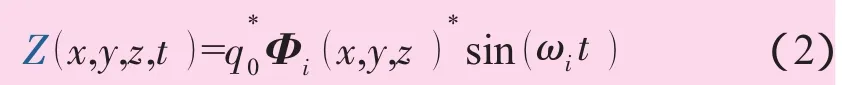
式中：Z（x,y,z,t ）為葉片表面各點的位移矢量；Φi（x,y,z）為葉片的第i階振型矢量；q0為廣義坐標振幅；ωi為第i階振型的固有頻率。

2 氣動控制方程

假設葉片在做簡諧振動的情況下引入運動網格，并對柱坐標系下的雷諾平均N－S方程進行求解來得到振動葉片所受到的非定常氣動力以及氣動力所做的功。

柱坐標系（φ，r，z ）下帶有角速度為ω和有限體積表面運動速度Vg（ug,vg,wg）的3維積分型N－S方程為

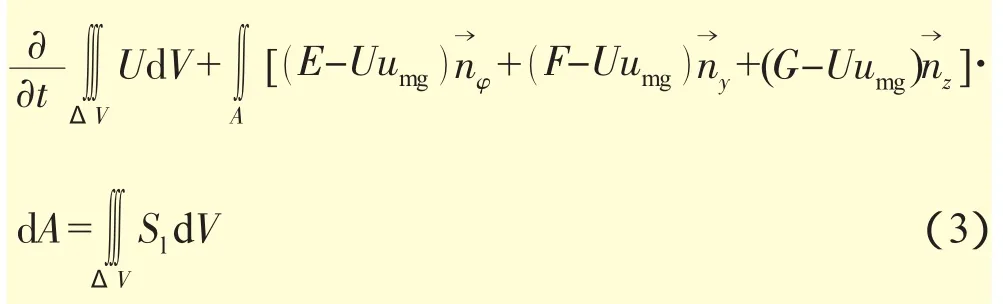
式中：U為氣動參數；E、F、G為無黏通量；Sl為源項。具體表達式見參考文獻[7]。

湍流模型采用對分離模擬較好的SST模型[4],方程求解采用CFD軟件FLUENT。

3 能量法-氣動功

考察在1個振動周期內，流體與葉片發生能量交換，如果非定常氣動力對葉片作正功，則葉片從氣流中吸收能量，發生顫振[8]。

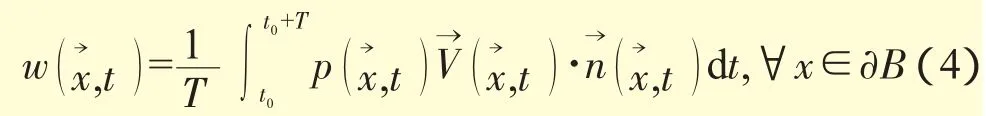
整個葉片的氣動功為葉片單位面積上1個周期內氣動功在葉片表面上的積分

定義等效模態氣動阻尼[10]

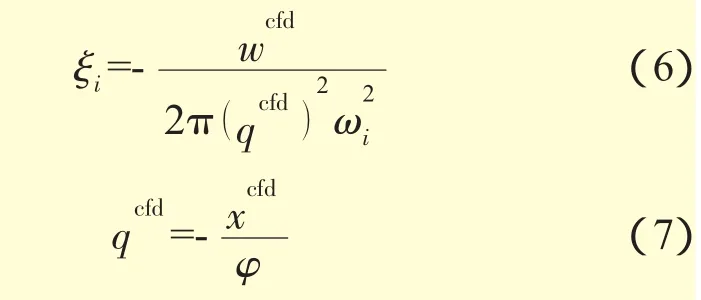
式中：xcfd為葉片實際振幅；φ為模態振幅。

按照上述的能量法，當非定常氣動力總功為正值時，模態氣動阻尼為負，葉片振動發散。

4 CSD/CFD數據插值

由于氣動計算網格比結構計算網格密，如圖1、2所示，要進行氣動與結構耦合計算，快捷、高質量的插值方法對計算時效和計算精度至關重要。本文改進了文獻[9]中的3維線性插值算法，在程序中引入面積控制因子，減小了插值誤差。該算法易懂，比復雜插值方法效率高。非常適用于非結構網格的計算。

圖1 CSD網格

圖2 CFD網格

該算法每個CFD格點選距離最近的10個FE網格點，引入面積控制因子選出其中不小于其值的最近的4個點，4個FE網格點每3個就可以組成1個平面三角形，求得每個平面三角形的單元中心，選定單元中心離CFD網格點最近的三角形平面作為插值平面△A1B1C1，如圖3所示。

圖3 FE網格點可選擇插值面

每個CFD網格點沿選定平面法向量投影如圖4所示。

圖4 CFD網格點投影到插值面

在點 A1、B1、C1上 分別作△A1B1C1的法線，使得 A1A2、B1B2、C1C2分別為點 A1、B1、C1的位移值。過點F做△A1B1C1的法線，在△A1B1C1和△A2B2C2上的交點分別為F1、F2，則F1F2為F點的位移值。如圖5所示。

用Fortran編制插值程序，對NASA R67葉片前6階模態進行了驗證，都得到了很好的結果。以下僅以第1階模態X方向的位移為例。插值前FE網格第1階模態X方向位移如圖6所示，插值后CFD網格模態位移等值線如圖7所示。從圖中可見，插值前、后數值一致。

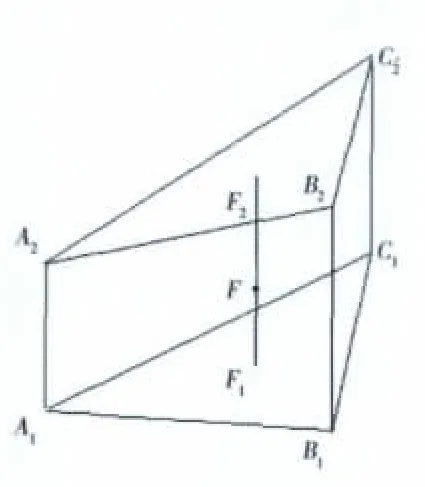
圖5 3維線性插值

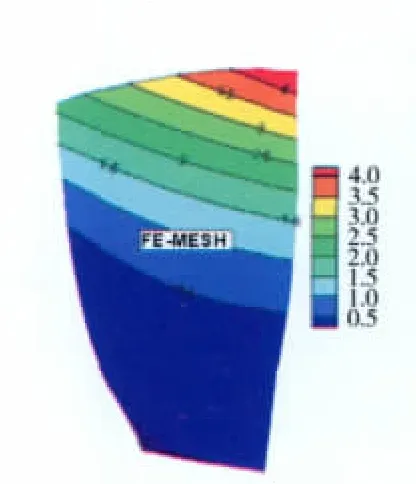
圖6 固體域FE網格第1階X方向模態位移

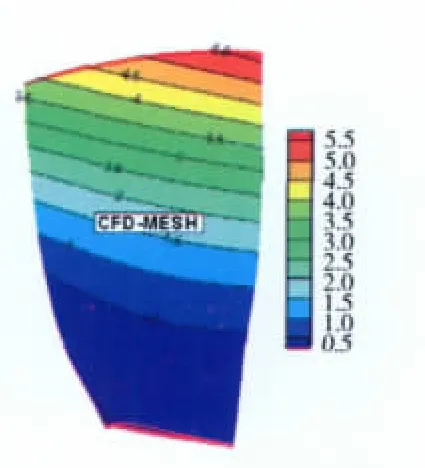
圖7 流體域CFD網格插值結果

5 動網格模型

在葉片氣動彈性仿真計算中，葉片表面各節點每個時間步以某階模態振型按固有模態頻率做正弦運動，這樣由于結構變形，每一計算時間步，周圍流場需要生成自適應的計算網格。本文編制UDF程序用DEFINE_GRID_MOTION（）宏命令指定葉片表面各節點的運動形式，實現葉片的某階模態振動。

由于計算模型單元數較多，非定常計算量大，為保證黏性計算精度和葉片表面附近網格隨著葉片振動畸變小，采用彈簧光順動網格模型，更新葉片周圍流場網格。彈簧光順網格模型更新過程如圖8所示。

圖8 彈簧光順網格模型更新

6 算例與結果

6.1 NASA R67風扇葉片定常場計算與結果分析

本例計算模型選取1個扇區通道，對稱面加周期邊界條件，如圖9所示。采用6面體非結構網格，共317833個節點，299509個單元；葉片表面10198個節點，10072個單元。不考慮葉尖間隙的影響，壁面設定為絕熱條件。為了加速收斂，計算采用多重網格技術，V循環。在定常狀態下，入口總壓為1個標準大氣壓，風扇葉片轉速按照設計轉速給定，通過改變流量得到風扇性能曲線。試驗得到的堵塞流量為34.96 kg/s，計算得到的堵塞流量為34.77 kg/s。不同流量下總壓比計算值與試驗值[12]的對比如圖10所示，試驗值和計算值分別按照各自的堵塞流量進行規一。從圖中可見，二者吻合較好，但是總體上計算壓比值比試驗值稍低。近最高效率點下的計算值和設計值見表1。從表中可見，二者誤差較小。

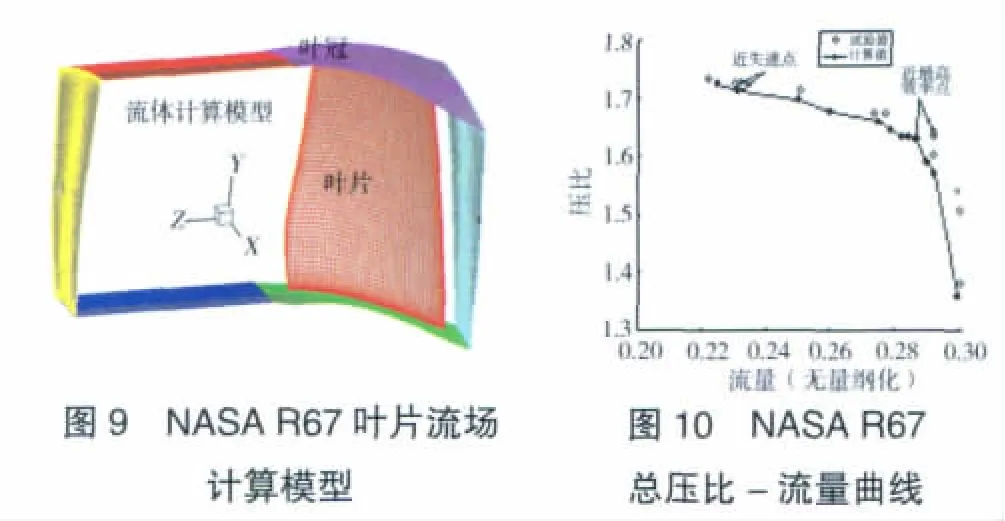
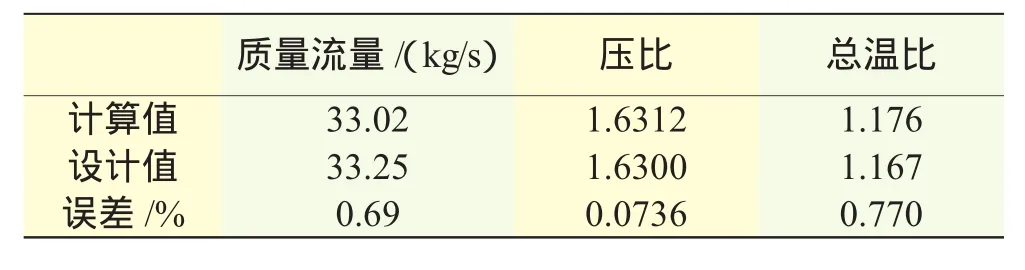
表1 NASA R67定常計算結果

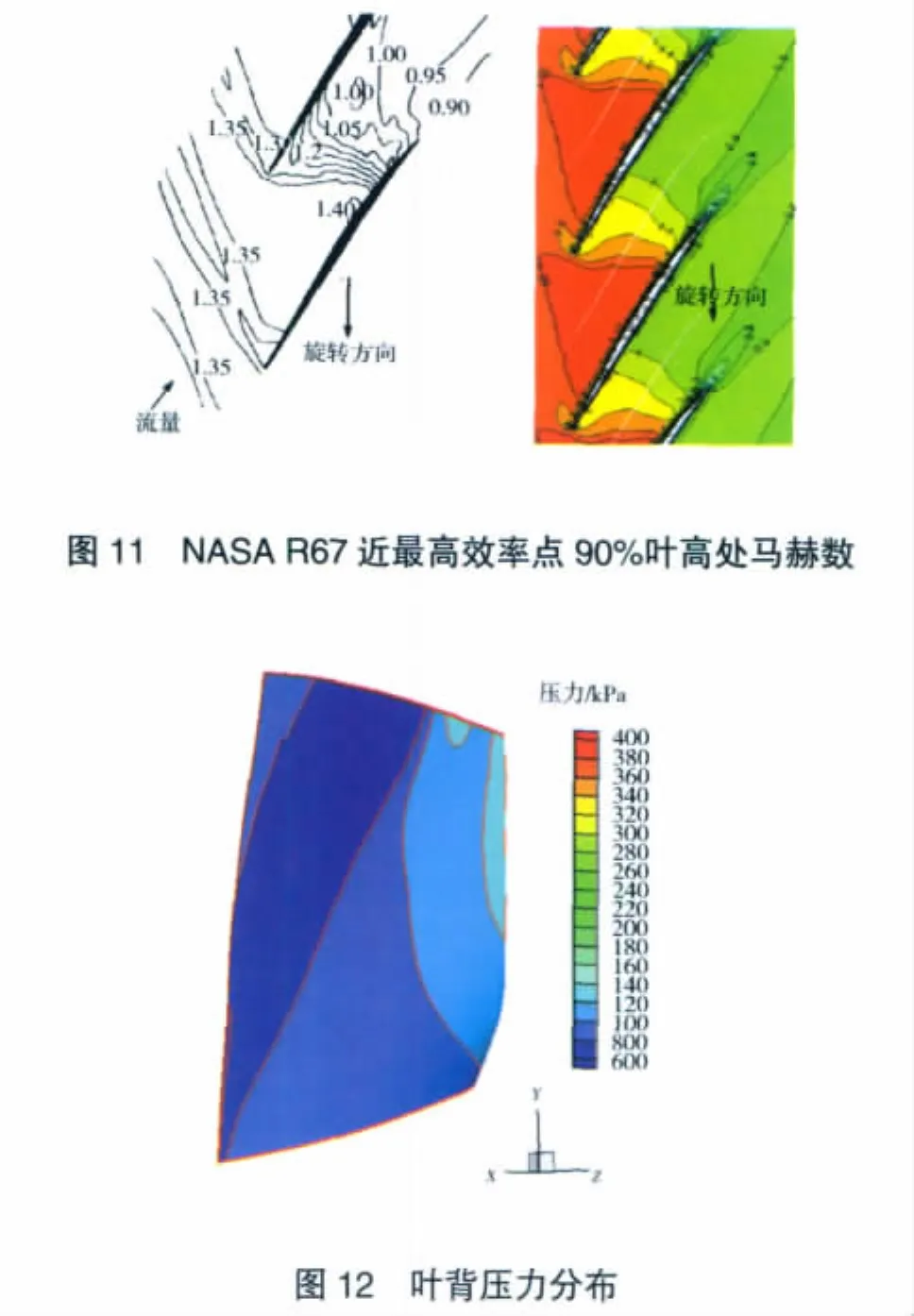
近最高效率點90%葉高處馬赫數如圖11所示。從圖中可見，90%葉高處葉片前緣斜激波和葉道中的垂直波呈“λ”形狀，同時還可以觀察到緊靠垂直激波后面有1道弱激波。

在設計轉速下，葉片前緣壓力值比后緣的低，吸力面上的激波波腳呈明顯的λ形，如圖12所示。

6.2 NASA R67葉片氣彈穩定性計算與結果

6.2.1 NASAR67葉片有限元計算

葉片模型單元類型為solid45，X、Y、Z 3個方向共2×20×22個單元，共1449個節點。考慮離心力，轉速為 16043r/min，泊松比 μ=0.3，彈性模 E=1.12E+11，選取鈦合金材料密度ρ=4440 kg/m3。約束方式為葉根固支全約束，葉尖自由。葉片模態和頻率如圖13所示。

6.2.2 第1階模態下葉片周期氣動功分布

品牌農業區域效應逐步顯現。臥龍區通過發展龍頭企業、培育農業品牌等舉措，充分發揮品牌農業企業的產業鏈優勢，提高標準化、區域化、產業化經營水平，提高農業經濟整體效益，有力地推進區域經濟的增長。如石橋的月季，現已發展到臥龍區的各個鄉鎮；石橋的老姜歷史悠久，姜質優良，在石橋的各個村都有不同規模的種植；謝莊龔河的玫瑰花、董營的紅薯已發展到周邊村種植；蒲山的桃、潦河坡的石榴、潦河的葡萄等因特色不同，形成了不同的旅游觀光區，而且由于產品品質優良，在南陽乃至武漢、上海等大中城市備受歡迎，品質優良價位高，品牌效應有所顯現。

本文計算了前3階模態氣動功分布，限于篇幅僅給出第1階彎曲模態下耦合計算結果。

將有限元結果插值到如圖2所示的CFD網格節點上，得到葉片表面位移數據，調用FLUENT動網格模型和UDF程序，并對模態位移進行歸一化，指定流場中葉片實際最大振幅為1 mm進行葉片第1階模態振動下的非定常計算。葉片前3階模態振動下的總氣動功和氣動阻尼見表2。

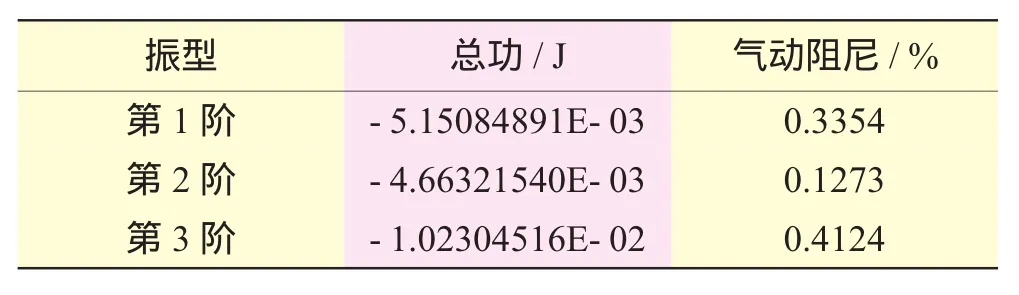
表2 前3階模態氣動功和氣動阻尼比

根據能量法，由表2計算結果可知：前3階模態振動非定常氣動力對葉片作功為負，起到阻尼作用，系統能量耗散，葉片不會發生氣彈失穩。當振幅為1 mm時,在第1階模態（第1階彎曲）和第3階模態（第1階扭轉）下的氣動阻尼較大，在第2階模態（以彎為主的彎扭耦合振動）下的氣動阻尼較小。

在第1階模態下，葉片監視點位移與非定常氣動力隨時間變化如圖14所示，由圖14（b、c、d）中可見，非定常氣動力較振蕩葉片位移變化滯后一定相位角，該相位角是葉片表面非定常氣動功變化因素之一。為了便于比較，放大了氣動力幅值倍數。

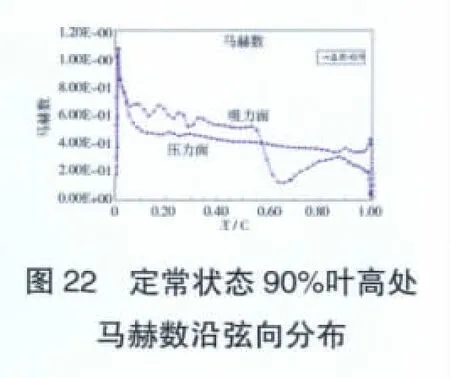
葉片壓力面和吸力面1個振動周期累積氣動功分布如圖15所示。在不同徑向位置（10%、30%、50%、70%、90%葉高），氣動功沿葉片弦向分布如圖16～20所示。文中選取定常場計算70%和90%葉高處相對馬赫數沿弦向分布作為激波參考位置，如圖21、22所示。

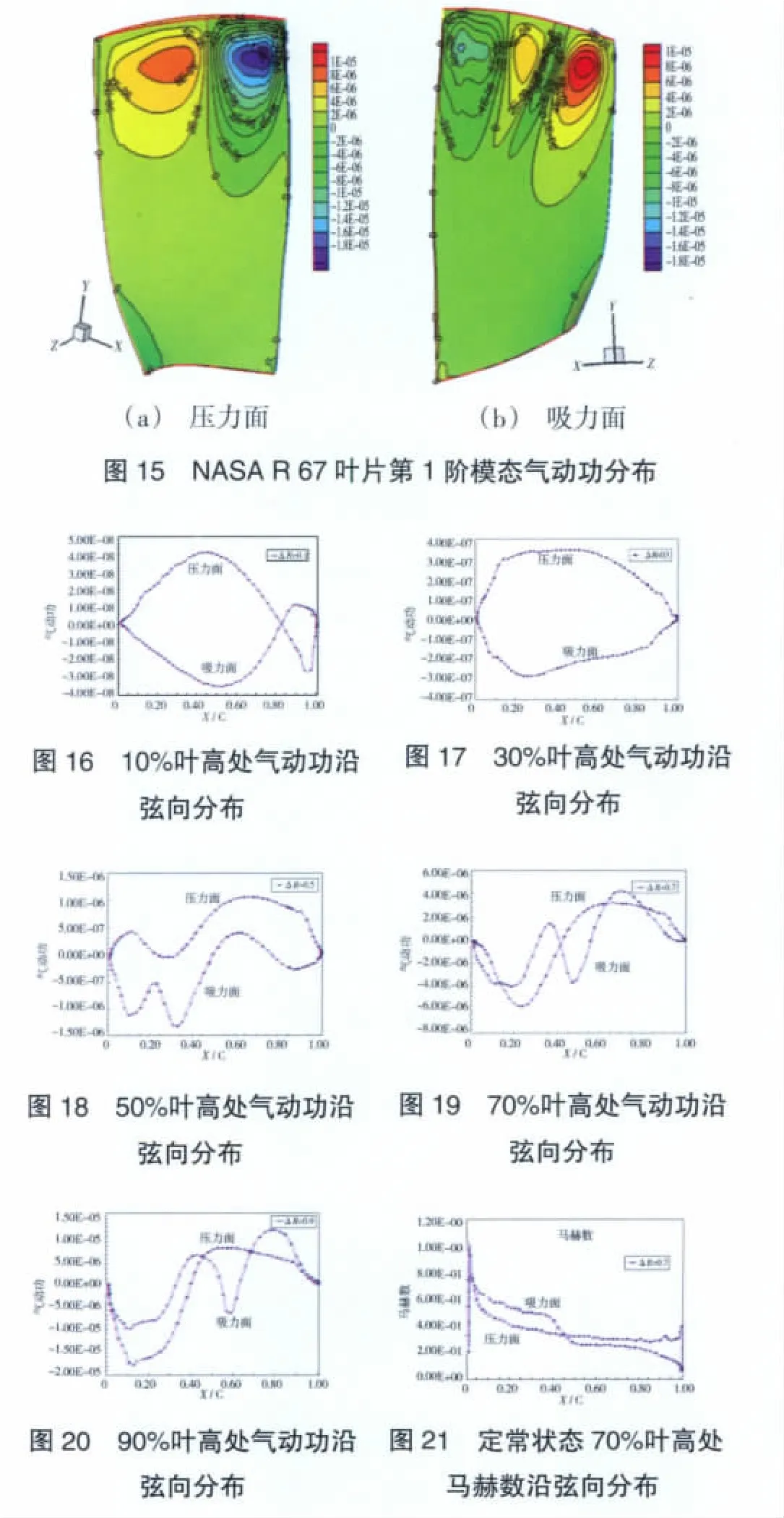
對比圖 15（a）、（b）可知，即使第1階彎曲振動葉片表面總的氣動功為負值，壓力面和吸力面局部仍存在氣動功為正值的區域（約70%～90%葉高，弦向0.6～0.9區域），對此應予以關注。

從圖16、17中可見，在第1階模態振動、50%葉高以下，由于激波的減弱或消失，壓力面、吸力面氣動功沿弦向受激波影響小，基本呈對稱分布。

從圖19、20中可見，在70%、90%葉高處，壓力面、吸力面沿著弦向出現了絕對值較大的正功區。對比圖19、21可知，在70%葉高激波位置處（約弦向0.35），氣動功出現了波動；同樣，對比圖20、22可知，在90%葉高激波位置也出現了氣動功的波動。

由此可見，在跨聲速流動中激波的位置對葉片氣彈穩定性有較大影響。

7 結論

（1）在前3階模態振動下，非定常氣動力對葉片作負功，氣動阻尼為正值，葉片不會發生顫振。

（2）基于3維線性插值理論發展的CSD/CFD網格數據交換程序，可以實現流固耦合計算，該程序對網格限制性小，經對比發現插值結果誤差小，從而減小了數據傳遞帶來的結果誤差。

（3）使用Fluent動網格模型對振蕩葉片擾流進行了仿真計算，給出了葉片表面非定常周期氣動功的分布情況，可為預測顫振提供依據。

（4）通過分析不同徑向位置葉片沿弦線方向的氣動功分布得出：激波位置和位移、氣動力間相位角是影響非定常氣動功分布的重要因素。

[1]袁新，金琰，暢國勇.葉輪機械中流體激振問題的流固耦合研究[C]//第八屆全國空氣彈性學術交流會論文集，北京：中國空氣動力學會，2003：274-280.

[2]宋兆泓.葉片顫振[J].水利水電機械，2006（5）：45-52.

[3]蔣福慶.風扇-壓氣機亞、跨音失速顫振的發作機理及預測技術[J].航空發動機，1996（3）：9-15.

[4]張陳安，史愛明，劉鋒，等.基于SST湍流模型的三維葉片氣動彈性問題研究 [C]//第十屆全國空氣彈性學術交流會論文集，北京：中國力學學會，2007：345-351.

[5]王延榮,郝燕平,宋兆泓.渦輪機械葉片顫振及其研究進展[C]//中國航空學會第九屆航空發動機結構強度振動學術交流會論文集，北京：中國航空學會，1998:265-271.

[6]徐敏，陳士櫓.CFD/CSD耦合計算研究 [J].應用力學學報，2004，21（2）：33-36.

[7]胡運聰,周新海.振動葉柵非定常流動數值模擬與葉片顫振分析[D].西安:西北工業大學,2003.

[8]趙瑞勇,楊慧，王延榮.葉片顫振數值模擬方法研究[D].北京:北京航空航天大學,2010.

[9]張瀟,王延榮.基于能量法的葉片顫振邊界預測方法[D].北京:北京航空航天大學,2008.

[10]Moffatt S，Li He. Blade forced response prediction for industrial gas turbines,Part 1: methodologies[R].ASME 2003- GT- 38640.

[11]楊策,老大中,蔣滋康.風扇轉子在設計轉速下內部流場的數值研究[J].自然科學進展,1999,9（增刊1）：1312-1317.

[12]Anthony J S, Jerry R W, Michael D H，et al. Laser anemometer measurements in a transonic axial- flow fan rotor [R].NASA- TP- 1989- 2879.