地球重力場模型在GPS高程測量中的應用*

原喜屯

(西安煤航信息產業有限公司,陜西西安710054)

0 引 言

在GPS高程測量中,通常的做法是利用水準點對似大地水準面進行曲面擬合,進而求得GPS網中所有待測點的正常高。由于這種方法需要聯測一定數量、分布合理均勻且能有效覆蓋整個擬合區域的GPS水準點,水準點聯測的工作量較大,在水準點稀少的測區實施起來也比較困難。利用EGM2008模型能以較高的精度將GPS測定的大地高差轉換為正常高差,測區內既不需要聯測GPS水準點也不需要測量正常高差,只需少量已知水準點就能夠解決測區所有GPS點的高程測量問題。

1 EGM2008模型的引進

1.1 EGM2008模型介紹

2008年4月,美國國家地理空間情報局在充分利用最新數據的基礎上研制并發布了新一代地球重力場模型—EGM 2008地球重力場模型(階次分別為2190,2159)。EGM2008模型是美國國家地理空間情報局(NGA)經過多年的研究和總結,在以往構建地球重力場模型的經驗和理論基礎上,采用最先進的建模技術與算法,以PGM2007B(PGM2007A的變種模型)為參考模型,利用GRACE衛星采集的重力數據和全球5′×5′的重力異常數據,TOPEX衛星測高數據以及現勢性好、分辨率高的地形數據,結合精度高、覆蓋面廣的地面重力數據完成的最新一代全球重力場模型。

EGM2008模型研制周期長達4年之久,研制期間曾委托許多國家和地區對過渡模型進行了測試與評估,從而使其不斷趨于完善。表1的GPS水準點外部檢測結果表明,EGM2008模型具有很高的精度。

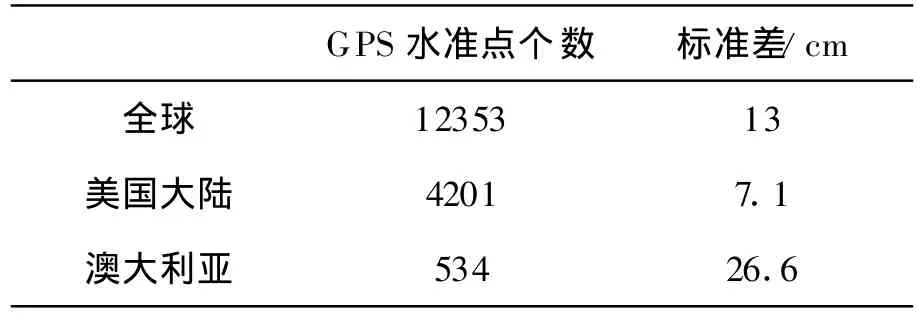
表1 EGM 2008模型GPS水準外部檢核結果

1.2 EGM2008模型在我國的適用性

章傳銀等利用全國858個A、B級、華北地區1305個、華南地區918個、華中華東地區4707個GPS水準數據對EGM 2008模型(無潮汐基準模型)進行外部測試。結果顯示,EGM 2008模型在我國大陸的精度與EGM 2008模型在全球范圍內的精度相當;EGM 2008模型高程異常在我國大陸的總體精度為20 cm,華東、華中地區為12 cm,華北地區達到9 cm,西部地區為24 cm.

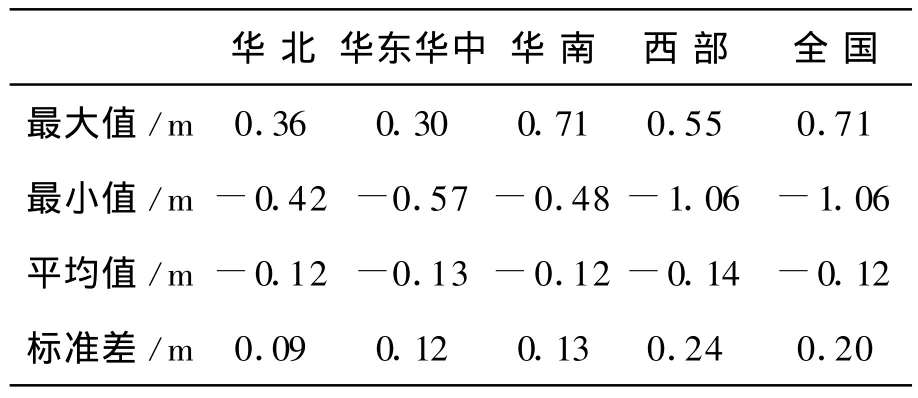
表2 EGM 2008不同階高程異常與GPS水準高程異常的比對結果/m

通過EGM2008模型可以獲得高精度高程異常值,使得GPS高程測量的精度大大提高,為了研究利用EGM2008模型進行GPS高程測量和測區內水準點數量和空間分布的關系對測量精度的影響,采用EGM2008模型(Und min1x1 egm2008 Nmax2190 MeanTide TP global)獲取高程異常,對試驗區內的數據分五種方案進行計算,將各種方法的GPS高程測量成果與水準高進行比較、分析。

2 應用試驗及數據分析

2.1 試驗區介紹

試驗區選取某條高速公路帶狀區域,某條高速公路地處山區,主線全長約100 km,公路自北向南,呈東北-西南走向,經過地段為平原、低山區,高山區,平均海拔1050 m,最低海拔800 m,最高海拔高程為1300 m,最大相對高差約為500 m.測區內有前期沿擬建公路布設的GPS控制點85個,所有控制測量均聯測四等水準。

2.2 試驗方法與結果統計

通過與C級GPS控制點聯測求得所有控制點的準確地心坐標,獲得控制點的大地高;采用EGM2008模型(Und min1x1 egm2008 Nmax2190 MeanTide TP global)獲得控制點的高程異常。GPS高程測量的公式:Hγ=H-ξ(注:Hγ為正常高,H為大地高,ξ為高程異常)。

方案A:利用控制點的大地高和EGM2008模型獲得的高程異常值進行計算求得控制點的正常高。計算結果為:85個待測點中轉換高程與已知高程之差最大為-21.9 cm,平均為-15.9 cm,中誤差為-23.1 cm.

方案B:用測區一端的1個控制點(共1個)的水準高作為約束條件,對方案A計算所得的結果進行改正,獲得所有控制點正常高。計算結果為:85個控制點與已知水準高之差最大為12.9 cm,平均為7.1 cm,中誤差為10.6 cm.

方案C:用測區中部的1個控制點(共1個)的水準高作為約束條件,對方案A計算所得的結果進行改正,獲得所有控制點正常高。計算結果為:85個控制點與已知水準高之差最大為10.8 cm,平均為5.6 cm,中誤差為8.6 cm.

方案D:測區兩端段各取的1個控制點(共2個)的水準高作為約束條件,對方案A計算所得的結果進行改正,獲得所有控制點正常高。計算結果為:85個控制點與已知水準高之差最大為6.5 cm,平均為2.7 cm,中誤差為4.3 cm.

方案E:測區兩端、中間各取的 1個控制點(共3個)的水準高作為約束條件,對方案A計算所得的結果進行改正,獲得所有控制點正常高。計算結果為:85個控制點與已知水準高之差最大為5.3 cm,平均為2.2 cm,中誤差為3.1 cm.

方案F:沿測區均勻選取5個控制點(共5個)的水準高作為約束條件,對方案A計算所得的結果進行改正,獲得所有控制點正常高。計算結果為:85個控制點與已知水準高之差最大為3.8 cm,平均為2.0 cm,中誤差為2.8 cm.

方案G:沿測區均勻選取6個控制點(共6個)的水準高作為約束條件,對方案A計算所得的結果進行改正,獲得所有控制點正常高。計算結果為:85個控制點與已知水準高之差最大為3.7 cm,平均為2.0 cm,中誤差為2.6 cm.

方案H:沿測區均勻選取12個控制點(共12個)的水準高作為約束條件,進行常規的高程曲面擬合計算,求得控制點的正常高。計算結果為:85個控制點與已知水準高之差最大為17.6 cm,平均為6.9 cm,中誤差為12.6 cm.

計算高程與水準高差值具體分布見表三。

從表3數據進行分析可以看出,方案A計算高程與水準高之差未呈現偶然誤差的分布特征,說明該方法存在系統偏差,統計精度與前文引用文獻的結論一致;方案B、C計算高程與水準高之差的分布未呈現偶然誤差的分布特征,說明該方法存在系統偏差,但測區內僅用1個GPS水準點就可以使計算正常高的最大誤差控制在10 cm左右,優于方案H中采用12個水準點進行曲面擬合的結果,因約束點處于測區中央方案C的結果稍優于方案B;方案D、方案E計算正常高與水準高呈現偶然誤差的分布特性,而且轉換精度較取方案B、C有所明顯提高;方案F、方案G水準點數量增加了,但計算精度提高不明顯。

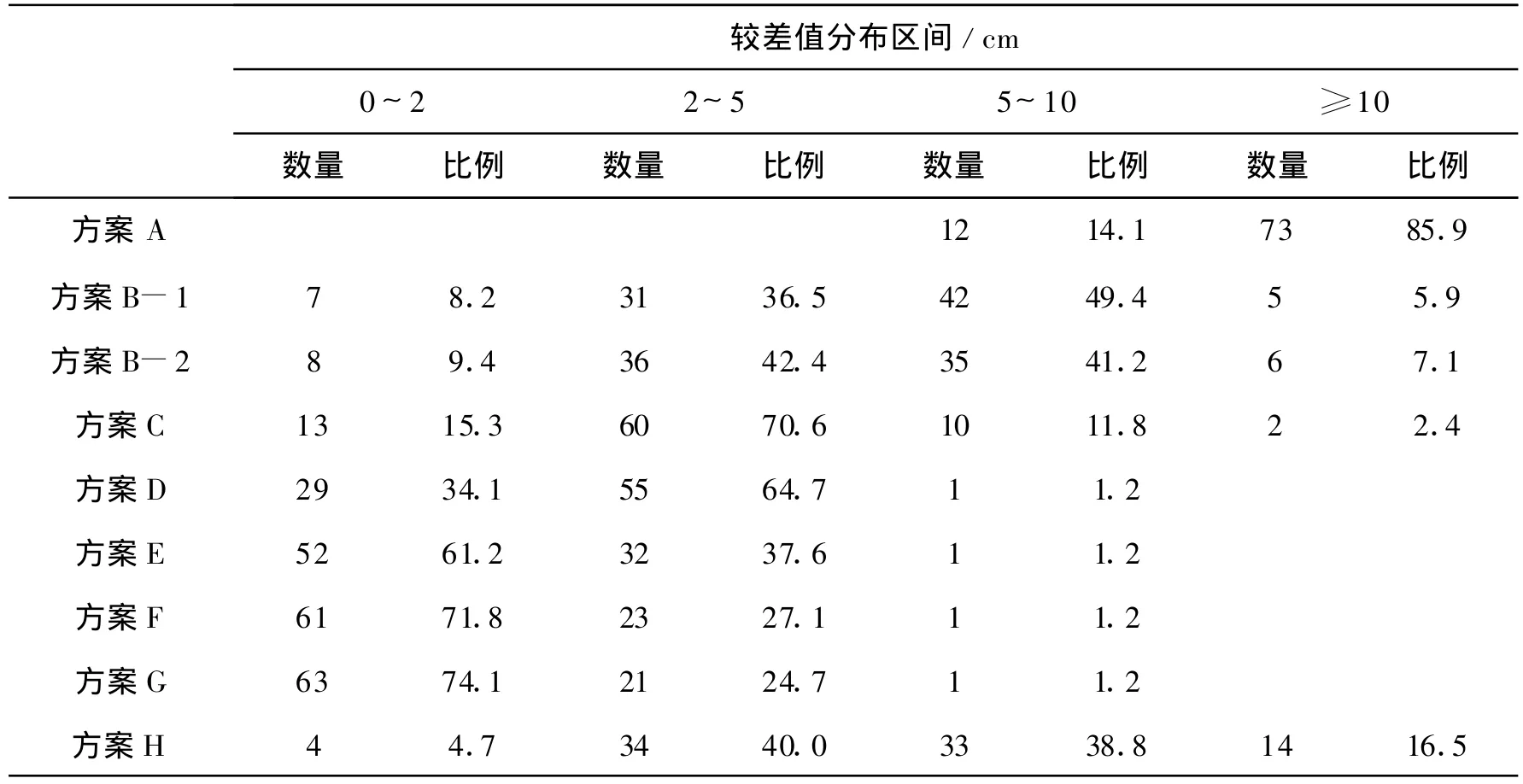
表3 計算高程與水準高差值統計表

3 結論與展望

綜合以上分析,可以得出以下幾點結論:

1)基于EGM2008模型的GPS高程測量對GPS水準聯測點數量要求較少,可以解決已知點少而測區大的GPS高程測量問題,且轉換效果較好。

2)基于EGM2008模型轉換GPS高程,對于較大測區,一般需要3～5個GPS水準點,再增加已知點數對提高轉換精度意義不大。

3)基于EMG2008模型的GPS高程測量,完全能達到等外水準測量的精度要求,可以用于各種比例尺地形圖測圖以及其他一些高程測量精度要求不太高的行業和部門。

基于EGM2008模型的GPS高程測量,在較大的測區范圍內僅用很少量的GPS水準點(至少為1個),就可以獲得令人滿意的轉換結果。通過不同方案的計算表明,利用EGM2008實現GPS高程測量,不僅可以降低對GPS水準點數量和分布的要求,而且能夠消除在擬合時的某些系統偏差,提高擬合精度,有時還能起到檢查GPS水準點高程的作用。

統計數據顯示,基于EGM2008模型的GPS高程測量有能夠達到四等水準測量的可能,如果在GPS大地高差轉換為正常高差時,能夠利用更高精度的國內模型,那么GPS高程測量將可以達到四等水準的精度。

EGM2008模型的精度高于國內已有地球重力場模型,在區域似大地水準面精化中可首選其作為參考重力場模型。在缺乏地面重力數據以及數字地形模型的區域,基于EGM2008模型的區域似大地水準面確定方法具有較好的應用價值,有望獲得更好的結果。

[1] 章傳銀,郭春喜,陳俊勇,等.EGM2008地球重力場模型在中國大陸適用性分析[J].測繪學報,2009,38(4):283-289.

[2] 馮林剛,楊潤甫,李 勝,等.基于EGM96的GPS高程轉換方法[J].測繪通報,2006(3):22-23.

[3] 章傳銀,黨亞民,晃定淀,等.似大地水準面誤差分析與抑制技術[J].測繪科學,2006,31(6):26-29.

[4] 張興福,劉 成,劉紅新,等.利用GPS/水準數據檢核EGM2008重力場模型的精度[J].測繪通報,2009(2):7-9.

[5] 李征航,黃勁松.GPS測量與數據處理[M].武漢:武漢大學出版社,2005.