《數值方法》課程理論與實踐教學改革探究

余承依，陳躍輝 （漳州師范學院數學與信息科學系，福建 漳州363000）

隨著計算機和數值計算技術的發展以及它們在生產生活中的廣泛應用，科學工程計算已成為科學實踐的重要手段之一。《數值方法》作為介紹現代科學與工程計算中常用的計算方法的一門課程，受到越來越多院校的重視，相繼成為了各高等院校理工科本科生和研究生的專業課程。從 《數值方法》研究對象可以看出，《數值方法》不像純數學那樣只研究數學本身的理論，而是把理論體系與計算機應用緊密結合在一起的實用性、服務性很強的課程。隨著現代課程體系的改革和深入，應用性人才的培養越來越引起人們的重視，傳統的教學方法和手段已經不能適應數值方法課程的培養目標，需要結合現代的教育技術觀念進行改革［1-2］。下面，筆者結合建設 《數值方法》精品課程過程中的經驗和體會對 《數值方法》理論與實踐教學提出了幾點改革建議??漳州師范學院精品課程建設項目。。

1 注重課程中的思想和方法

《數值方法》很多內容在 《數學分析》、《高等代數》、《微分方程》等課程中都學過，但 《數值方法》更注重應用性，其思想方法較傳統的數學課程相比發生了較大轉變。

1）離散化思想與方法 《數值方法》中各種連續性變量的求解問題都要轉化為離散問題求解，不同的離散化方法得到不同的數值求解方法，因此教師授課時要引導學生從微積分中連續的思維模式轉變到離散的思維模式下，講清楚離散化的基本思想，如數值積分、微分方程數值解等涉及到眾多的離散化問題。

2）近似計算思想與方法 傳統的數學中強調邏輯的嚴密性和數學計算的準確性，但科學工程計算中所接觸的數據可能是帶有舍入誤差的近似數據，涉及到的很多數學問題無法求出準確解，只能被具有一定精度的近似解替代，且經典完美的求解析解的方法在數值求解中也不一定適用，故近似計算在數值計算過程中成為了一種有效的方法和手段。

3）逐次逼近的思想與方法 逐次逼近的思想與方法是 《數值方法》課程中的重要內容之一，很多數值方法都依賴于逐次逼近的思想與方法。

4）函數逼近的思想與方法 插值法、數值積分與微分中涉及到眾多的函數逼近思想，微積分中所討論的定積分的計算，主要是針對被積函數的原函數可以用初等函數表示且易計算。但這類積分只有很少部分，在實際問題中得到的很多積分的被積函數的原函數無法用初等函數來表示，即使能表示也很復雜，不易計算，這時對被積函數的各種不同的函數逼近方法就可以得到很多不同精度的數值積分公式。

《數值方法》課程的教學過程中要始終貫穿這些思想和方法，對涉及到的這些思想和方法的深刻理解有助于對課程知識的理解和把握。

2 優化教學內容，融入知識背景和數學建模思想

1）優化教學內容 《數值方法》作為介紹科學計算中的基礎理論與基本方法的課程，已成為眾多專業學生的必修或選修課程。針對不同專業和不同層次的學生，首先結合學生的實際情況和課程的要求制定合理的教學大綱和考試大綱；其次應對現有教材內容進行加工，做到所講授的內容既保證知識的完整性、理論的系統性，又體現不同專業方向對數值方法課程的不同要求［3］。

對于數值方法，學生普遍感到難學，面對眾多的數學公式，不在乎能記住多少，關鍵是構造各種算法的思想和如何運用算法來解決實際問題。對計算機專業側重如何運用算法解決實際問題，可以采用已有的專門的數學軟件包教學，如Matlab等，計算數學專業注重算法的構造和細節推理過程，宜采用C語言教學。

2）融入背景知識 《數值方法》課程具有很強的科學工程計算背景，傳統的數值方法課程教學中忽視了知識背景的教學。講授純科學只能教給學生知識，而融入背景知識卻能教給學生更多智慧。介紹一些經典算法的歷史背景和一些常用的數值計算方法工程背景，往往可以引發學生對于學習意義的深入思考，原本較為枯燥的課程內容也會因此變得生動有趣，激發同學們的學習積極性。例如在講授插值，擬合等問題時可以結合社會生活中的經濟數據的預測等教學。

3）融入數學建模的思想和方法 為了凸現實用性，在課程改革和建設過程中注重與其他學科的融合，主動融入數學建模的思想和方法。很多數學模型最終都要借助于數值方法課程中的各種理論、算法來求解，如果精選一些既涉及到數值方法理論和算法又能體現數學建模思想的內容，將兩者有機結合起來，從實際要解決的問題出發，建立數學模型，然后結合 《數值方法》課程中相關理論、算法研究解決數學問題。《數值方法》課程中融入數學建模思想和方法，為數值方法找到了實際的應用背景，體現了數值方法的實用性。

3 注重上機實驗教學

1）重視算法構造和上機實現 《數值方法》課程中多種算法及其理論分析結果，只有通過上機實驗才能得到驗證，也只有通過上機運算后才能更好地更深刻地理解和掌握。在算法的構造過程和理論分析介紹完之后，當需要用實例驗證說明算法時，要通過實驗引導學生結合實例將算法逐步轉化為對應的高級語言源程序，并調試、運行。

2）精心設計實驗題目 上機題目的選擇安排至關重要，一方面要體現該課程的重點與難點，另一方面又要具有一定的探索性。緊密結合 《數值方法》課程，尋找理論知識所能解決的實際生活和生產中的實際問題，通過問題的解決幫助學生理解和鞏固所學的理論知識。既有基礎性的實驗，也有專題性的實驗，又有綜合性的實驗；既有統一布置的題目，又有鼓勵學生根據自己的專業、能力選擇其他的開放性題目。要求對同一題目盡可能的采用不同的算法設計，從病態性、敏感性及計算復雜程度等方面來分析每種算法的優缺點，加深對算法的理解。

例如在講授非線性方程的數值解這一章中的不動點迭代法時，同學們都知道在求解非線性方程時高于5次的方程沒有求根公式可以利用。迭代法是一類重要的求解非線性方程數值解的方法，迭代法中最關鍵的問題是將方程f（x）=0轉化為等價方程x=φ（x），φ（x）稱為迭代函數。φ（x）選取的好壞直接關系到得到的迭代序列｛xn｝是否收斂到方程的真解x＊以及收斂速度的快慢，為了使學生充分理解這一點，在講完這一節后可安排如下的上機習題。

例1 已知方程x3＋4x2-10=0在 ［1，2］有唯一根，若選取迭代函數φ（x）為：

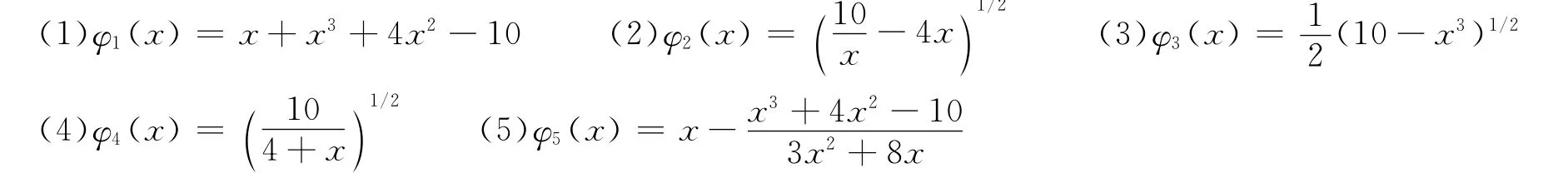
選取初值x0=1．5，對于φ（x）的以上5種選擇觀察不同的迭代效果。通過比較該實驗中的5種結果，學生很容易掌握迭代法的關鍵是迭代函數的選取，對于不同的迭代函數迭代的效果不一樣，有的發散，如 （1）和 （2）；有的收斂，如 （3）、（4）、（5），并且收斂的速度也不一樣，迭代函數 （5）收斂效果最好。這種方法剛好就是下一節所要講解的經典牛頓迭代法，這樣安排的實驗既有利于學生掌握本節知識，又能起到較好的銜接作用。

3）實行團隊合作的分組實驗教學 注重實驗的組織和管理，以項目為主導，實行分組教學，加強團隊合作。將學生分成實驗小組，教師給出一定范圍內的具有啟發性的實驗問題，各實驗小組根據教師指定的范圍結合學過的知識，在濃厚興趣的支配下自行設計方案，分析理論并上機實驗，最終解決問題。筆者曾在數學與信息科學系2009級學生中試用這種項目主導，團隊合作分組實驗教學法，將2個同年級的不同班級進行對比實驗教學。一個班級采用項目主導，團隊合作實驗教學的方式，學生的反應異常積極，由學生自行組合 （4～5人）成一個實驗小組，小組成員根據教師的實驗內容一起討論、研究問題的解決方案，分工合作，將一個復雜的問題分成幾個小問題，每個人負責一個方面的工作，大家完成以后組裝在一起形成最終的成果。每周的實驗課上由每小組派一名代表現場演示說明各自小組研究的成果，向同學介紹自己小組采用的方法以及獨特的地方。另一個班級采用傳統的單槍匹馬上機方法，學生個人獨立編制程序、調試。通過對比，2個班級的效果完全不同，前一班級每次都能按時完成任務，并能保證上機調試成功。而后一班級80%同學在課后都沒有抽出時間編寫程序，而是等到上機時才臨時編寫程序，匆忙之下寫出的程序調試很難成功，不易在規定的時間內完成任務，并且對在調試過程中出現的問題也沒有進一步深入探討。對比實驗教學結果說明以項目主導，團隊合作的分組實驗教學方式能充分調動同學們的積極性，激發研究興趣。學生利用課余時間查找有關的資料，學習課本中所沒有的其他專業知識，編制程序并反復實驗，確保實驗課上演示成功，培養了學生自我收集資料和主動學習的能力與習慣。另外，對于不同的課題內容，小組中必須派不同的代表演示說明，這樣小組成員之間就發展起了良好的合作關系，充分調動了小組中每位成員的積極性，每位成員都盡力為主講同學服務，同時下一次也同樣能感受到同小組其他成員的支持，這為學生以后走上工作崗位發揚團結協作精神奠定了良好的基礎。

4）制定合理的考核方法 實驗結束后學生及時對實驗總結，填寫實驗報告。教師從多方面多角度全面評價學生的實驗技能與創新能力。數值實驗的教學十分重要，實驗的選題、組織與管理、程序的設計編寫、結果的分析和學生的考核評價等每一個環節都要從嚴把關。只要精心設計出新穎的數值實驗，注重解決問題的思想與方法，勇于創新，就能取得較好的效果，成為為其他課程服務的有力工具。

4 嘗試開放式教學模式

傳統意義上教師講解、學生聽課的方式不利于激發學生的學習興趣。對于一些新知識，教師可以不直接講解，以問題驅動［4］為主導，老師通過提出相關的問題，引導學生積極思考，學生提出自己的見解，教師組織課堂討論，學生就不同的觀點發表意見，最終歸納總結學得知識，并得到問題的最優答案。對于這種方式獲得的知識學生理解最為深刻，但對教師的要求比較高，教師除了具有本課程的相關知識外，還應具有收集分析整理相關資料能力，能結合教學的內容有針對性地設計出合理的教學問題。教師在以問題驅動為主體的這種開放式教學模式中，教師是活動的組織者，有序的引導學生進行相關內容的討論是關鍵，在一種輕松融洽的學習氛圍中，推動學生不斷的質疑和思考，調動學生的主動探尋真理和學習的熱情。

《數值方法》課程公式復雜，傳統的教學模式效率低下，教學過程中宜采用多媒體課件為主，黑板板書為輔的教學手段［5］。通過多媒體演示增加課堂的信息量和感染力，展現出傳統黑板教學不能展現出的直觀、動態的效果。

［1］鐘爾杰，黃廷祝 ．關于數值分析課程教學改革研究的綜述和思考 ［J］．大學教學，2007，23（2）：8-12．

［2］宋松和，朱建民，唐玲艷，等 ．高等數值分析課程教學改革探討 ［J］．高等教育研究學報，2008，31（4）：66-67．

［3］孟國艷，趙青杉 ．計算方法課程教學改革探討 ．忻州師范學院學報 ［J］．2008，24（2）：111-113．

［4］陳煥禎，姜子文，劉尊東 ．計算方法課程改革與建設的探討 ［J］．山東師范大學學報 （自然科學版），2002，17（4）：88-90．

［5］李小林 ．關于數值計算方法課程教學改革的探討 ［J］．重慶文理學院學報，2010，29（2）：85-87．