兩輪機器人的舞步運動規劃和仿真研究

孫 亮，呼德夫

SUN Liang,HU De-fu

（北京工業大學 人工智能與機器人研究所，北京 100124）

0 引言

兩輪自平衡機器人屬于輪式機器人的范疇，這種機器人兩輪共軸，獨立驅動，作為差動驅動式，通過運動控制保持平衡，可直立行走。它結構簡單、運動靈活，適于在狹小和危險的空間內工作，具有較好的機動性。兩輪自平衡機器人屬于非線性、時變、欠驅動、非完整約束系統 。目前，兩輪機器人的自平衡控制方面的研究較多，常用DSP或單片機作為主控制器，陀螺儀和加速度計采集機器人姿態和傾角數據，同時電機編碼器采集車輪轉速數據，將數據傳到主控制器，通過卡爾曼濾波數據融合和PID算法來進行機器人車輪轉速控制，從而實現自平衡控制效果。兩輪機器人在實現自平衡的前提下可以完成多種動作。若機器人能夠響應舞曲優美的韻律，完成諸如華爾茲這樣的特定舞步動作，則會最大程度地體現出兩輪機器人動態性能好、機動性強的特點。本文基于兩輪機器人的基本運動方式，提出機器人完成簡單舞步動作的運動規劃，給出了基于有限狀態自動機的運動規劃描述方法，并用基于廣義雅可比矩陣的兩輪機器人分解運動速度控制算法 進行了仿真實驗。實驗結果表明算法具有良好的準確性與可靠性。

1 運動學模型

兩輪移動機器人的運動學模型如圖1所示。其中主要有：C為機器人車身前端一點；O為機器人平臺質心；b為兩車輪間距；r為車輪半徑；lc為點C與質心O點之間距離；φ為機器人車身傾角；θl和θr分別為左右輪轉角。

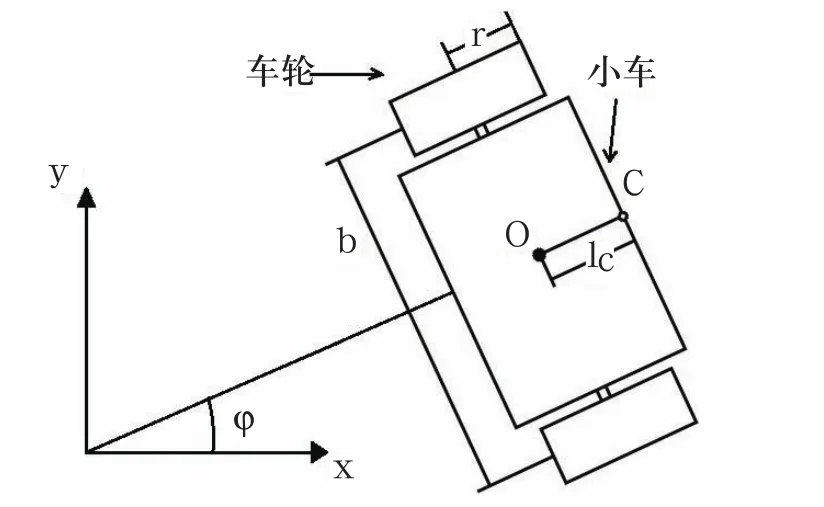
圖1 兩輪移動機器人幾何模型

J為兩輪機器人的廣義雅克比矩陣，反映機器人上點C速度與車輪轉速之間的關系[2]。

2 基于有限狀態自動機的運動規劃描述

為了規劃兩輪機器人的運動軌跡，使其按照華爾茲舞步軌跡運動，可以用有限狀態自動機來描述其狀態變化情況。有限狀態自動機（Finite State Automata,FSA）定義為一個五元變量組[3]，即：

其中，T為對應于基元的符號集合，Q為機器狀態集合，δ為映射關系集合，q0為機器的初始狀態，q0∈Q， F為終端狀態集合，F∈Q。

兩輪機器人的符號集合為：

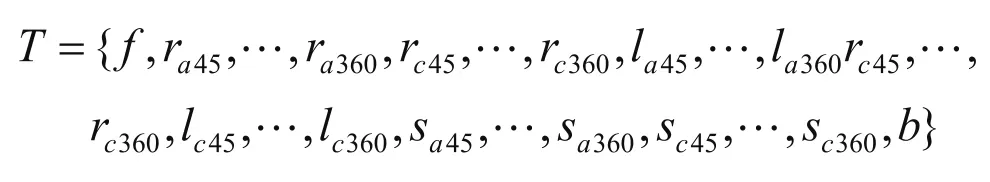
其中，f表示機器人前進（forward），b表示機器人后退（backward），r表示右輪以左輪為軸轉動，即轉動輪為右輪，同理l表示左輪以右輪為軸轉動，即轉動輪為左輪，s表示機器人無半徑自旋轉，c表示在俯視視角中機器人順時針（clockwise）轉動，即向右轉，a表示在俯視視角中機器人逆時針（anti-clockwise）轉動，即向左轉，45等數字表示其相應轉動的角度，所以ra45表示機器人右輪以左輪為軸逆時針轉動45°，即機器人左轉45°。其他的符號以此類推。

機器人狀態集合，即機器人車身朝向狀態集合為Q={F,B,L,R,FL,FR,BL,BR}

其中，F表示向前方向（Forword），B表示向后方向（Backward），L表示向左方向（Left），R表示向右方向（Right），FL表示左前方向，FR表示右前方向，BL表示左后方向，BR表示右后方向，如圖2所示。

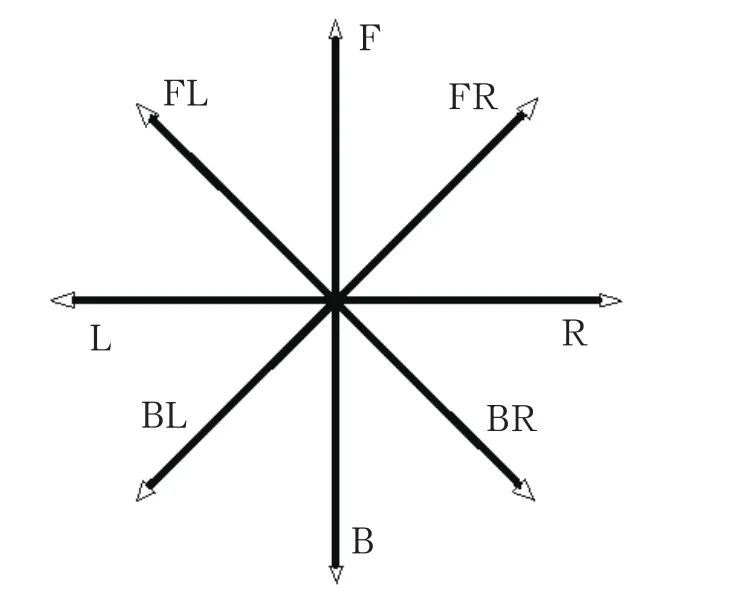
圖2 兩輪機器人舞步運動方向

在映射關系δ=(A,a)=B中：A表示轉移源狀態，為狀態Q的元素；a表示轉移要素或輸入信號，即符號集合T中的元素：B表示轉移終狀態，也為狀態Q的元素。

機器人的所有狀態遵循以下映射關系：

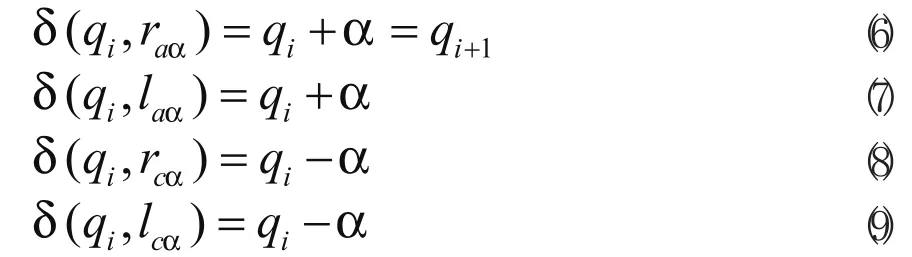
上式(5)中，qi表示第i時刻機器人的朝向狀態，當它收到raa符號指令（即機器人右輪以左輪為軸逆時針轉動α0）后逆時針轉α0，狀態變為qi+1，表示為qi+α。其他的映射關系以此類推，如式(7)-(9)所示。

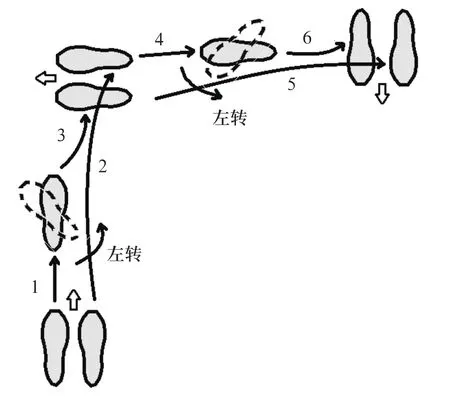
圖3 人的連續左轉舞步示意圖

下面以較為典型的華爾茲舞步——連續左轉為例，給出相應的有限狀態自動機描述方式。如圖3所示，人的連續左轉90°舞步由前進左轉90度和后退左轉90度組成，共可以分解為六個步伐。以男士步伐為例，在圖3中以向上方向為向前：

1）邁左腳前進；

2）再邁右腳，同時身體向左側身，開始左轉；

3）收回左腳，兩腿并攏，身體朝左，完成前進左轉90°；

4）退右腳后退；

5）再退左腳，同時身體向左側身，開始左轉；

6）收回右腳，兩腿并攏，身體朝后，完成后退左轉90°。

同理，如圖4所示，可以得到機器人的模擬舞步運動示意圖，分別模擬得到上述6個步伐：

1）左右輪勻速前進；

2）右輪繞左輪左轉（前進）45°；

3）左輪繞右輪左轉（后退）45°，完成前進左轉90°；

4）左右輪勻速后退；

5）左輪繞右輪左轉（后退）45°；

6）右輪繞左輪左轉（前進）45°，完成后退左轉90°。

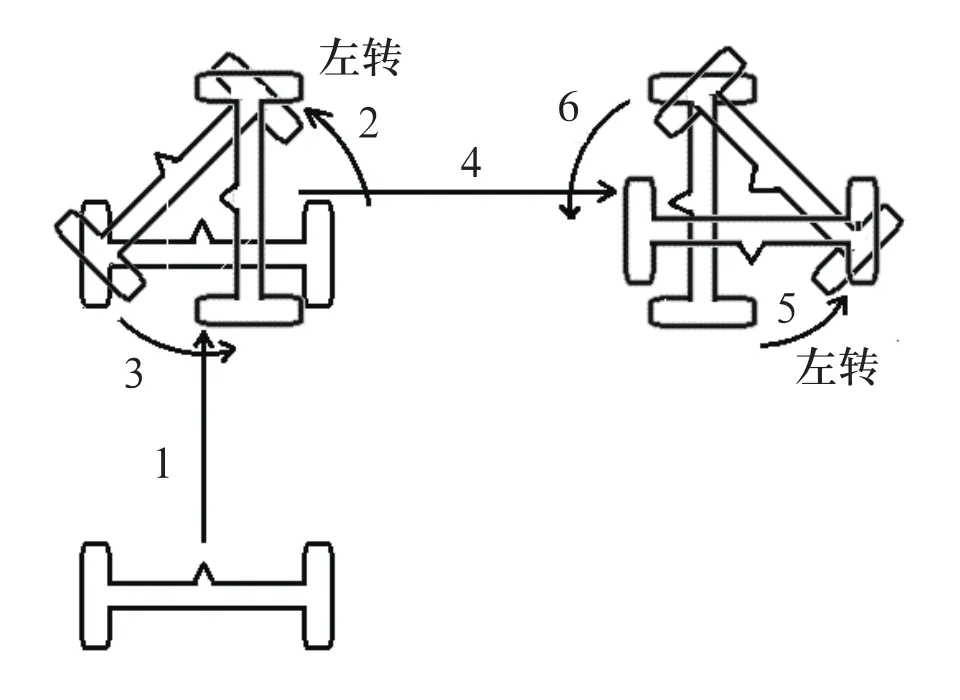
圖4 兩輪機器人模擬的連續左轉舞步示意圖

根據以上六個步伐分解，應用基于有限狀態自動機的舞步規劃方法得到連續左轉90度舞步的相應集合為：

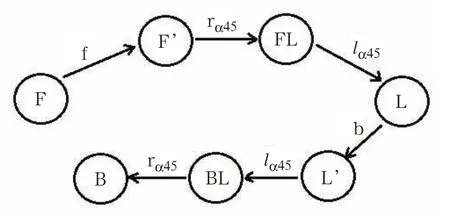
圖5 機器人連續左轉舞步的狀態轉移圖

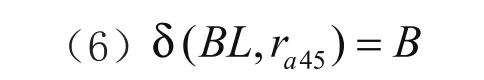
4）繪制狀態轉移圖。根據步驟3）中的映射關系，得到機器人舞步的狀態轉移圖，如圖5所示。

以此類推，可以得到機器人模仿華爾茲舞步的所有映射關系及其基于FSA的表達方式。

3 分解運動速度控制及仿真實驗

由式(4)可知，由機器人上一點C的速度也可以求出車輪轉速。此時車輪控制量如下：

采用計算機控制，該方程變為離散式。速度項可以表示為單位時間里（控制周期Δt）的位移增量， 即：

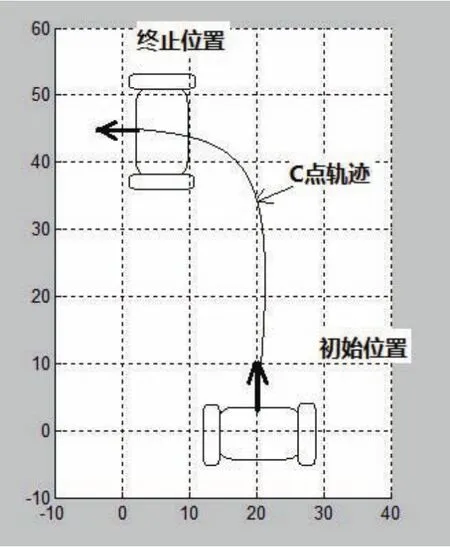
圖6 兩輪機器人的期望運動軌跡

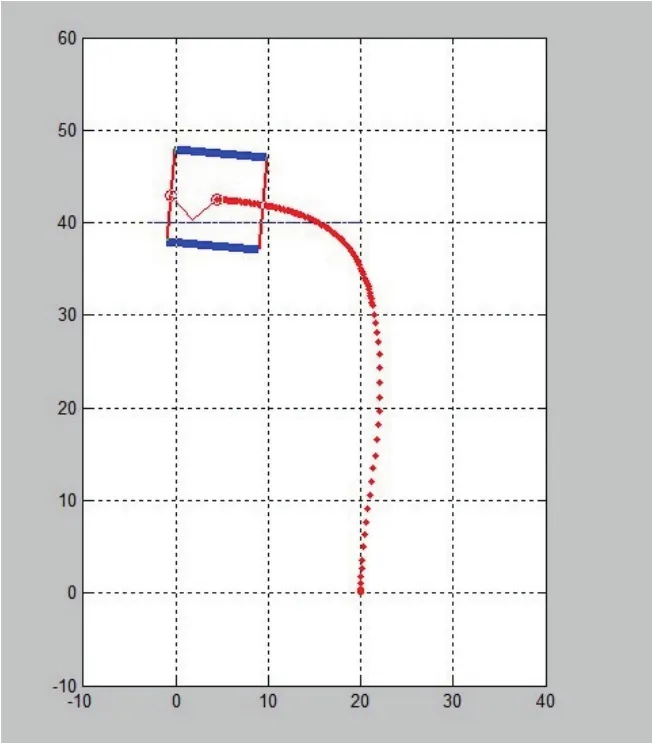
圖7 兩輪機器人運動軌跡仿真結果

式中：Δp為一個控制周期內的位移變化；ΔΦ為同一時間間隔內的角度變化。如果給定C點的軌跡，當Δt選定時，可以確定Δp，將其代人上式求出各個角度增量ΔΦ，可得到各個角度的給定值，最后由角度伺服控制系統去實現位置控制。差動驅動式移動機器人的分解運動速度控制是一種基于逆廣義雅可比矩陣的連續路徑跟蹤控制方法。該算法要考慮合理的控制周期，通過控制每個周期內的角度輸出量實現對軌跡的跟蹤或速度控制。

為了驗證本文提出的兩輪移動機器人運動規劃算法的正確性和可行性，在MATLAB平臺上做華爾茲基本舞步-左轉90°的模擬仿真實驗。為了能使機器人按照指定的軌跡運動并移到指定的位置，可以讓機器人跟蹤某種特定的軌跡[4]。機器人的參數取：b=1.5,lc=0.5,r= 1.3。

初始位置為(xc0,yc0,φ0)=(20,0,90o)， 終止位置(xc1,yc1,φ1)=(0,43,180o)，為了實現機器人車身左轉，使C點跟蹤近似軌跡為y=40。圖6給出了機器人平臺上點C的期望運動軌跡，圖7給出了兩輪機器人運動過程仿真結果。從仿真結果可以看出，控制算法使兩輪機器人驅動兩車輪轉動可以實現機器人車身上一點跟蹤預定軌跡，完成了基本舞步左轉90°的位置與方向角的相應改變。

4 結束語

本文用有限狀態自動機描述了兩輪移動機器人的舞步運動規劃。有限狀態自動機是具有有限狀態的離散輸入輸出的系統數學模型。華爾茲基本舞步動作是由若干個基本動作元素組合而成的，且這些元素都是較為固定的運動模式。所以可以用有限狀態自動機規范地描述兩輪機器人舞步的運動規劃。同時本文運用基于廣義雅克比矩陣的分解運動速度控制算法來實現機器人對軌跡的跟蹤和速度控制，并用MATLAB驗證了該算法的準確性。

[1] 王建俊.兩輪同軸機器人的自平衡控制研究[J].數字技術與應用,2010,7：105-106.

[2] 柳長安,李國棟,劉春陽.差動驅動式移動機器人的運動規劃[J].哈爾濱工業大學學報,2003,35(9)：1095-1097.

[3] 孫亮,禹晶.模式識別原理[M].北京：北京工業大學出版社,2009,2：54-56.

[4] Yoshio Yamamoto,Xiaoping Yun.Coordinating Locomotion and Manipulation of a Mobile Manipulator. IEEE Transactions on Automatic Control,1994,39(6)：1326-1332.

[5] SERJI H.A unified approach to motion control of mobile manipulators[J].The International Journal of Robotics research,1998,17(2)：10-15.