采用選擇性分段PCA算法的高光譜圖像異常檢測

趙春暉，胡春梅，石 紅

(哈爾濱工程大學 信息與通信工程學院，黑龍江 哈爾濱 150001)

高光譜圖像具有“圖譜合一”特性，成像波段密集且連續，具有很高的光譜分辨率，在檢測、識別地面的低空間分辨率目標方面具有獨特的優勢.異常檢測算法不需要利用光譜的先驗知識，而能直接檢測出與周圍景物光譜存在明顯差異的光譜信號所在位置作為異常點，由于目標先驗光譜信息很多實際情況下難以獲得，所以異常檢測算法對于未知場景中光譜特性未知目標的檢測識別具有重要意義［1］.常用的異常檢測算法主要有RX檢測算法，正交子空間算法(OSP)，約束能量最小化算法(CEM)，低概率檢測算法(LPD)等.利用高光譜圖像對目標進行檢測的常用算法通常在檢測之前先對圖像進行預期的處理，如將其投影到特征向量空間中，選取其信息量較大的波段用于后續的異常檢測，但是在預期處理的過程中往往會遇到這樣的問題:高光譜圖像各波段在成像過程中受波段響應特性、大氣吸收和成像系統噪聲等因素的影響不同，各波段反映的光譜特性不同，且相鄰波段具有很強的相關性，而在變換的過程中經常包含對各個波段中背景與目標之間光譜差異的加權或乘方加權等運算，由于地物光譜的復雜性，由不同的光譜特性所得到的最終運算結果可能相近［2］，且需要消除波段之間很強的相關性，并選取其中包含目標信息較多的波段用于異常檢測.因此，本文算法先將一組多維的高光譜數據根據波段間的相關性劃分成多組波段子集數據，并分別對每一波段子集進行特征提取，去除波段之間的相關性，這樣使得高光譜數據的可分性投影到了各波段子集上，然后在各波段子集中分別尋找出局部平均奇異度(LAS)最大的波段，并將其映射到高維的特征空間中，充分利用數據的高階統計量對目標進行檢測，最終實現異常檢測.

1 算法原理

1.1 選擇性分段PCA算法

本文算法主要思想是通過在各波段子集中選取局部平均奇異度最大的主成分用于后續的KRX異常檢測，使得在減少數據量的同時，最大限度地保留異常目標的信息，從而在降低計算復雜度的同時盡可能地提高檢測性能.算法實現流程如圖1所示.

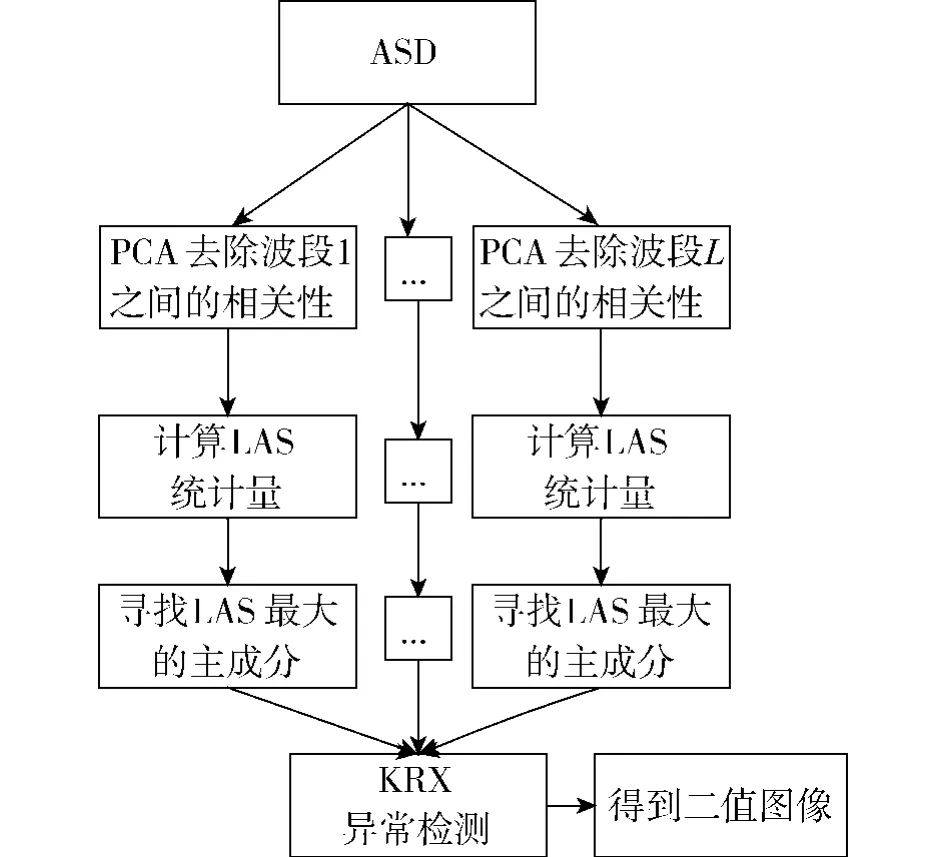
圖1 算法流程圖Fig.1 Algorithm flowchart

高光譜圖像各波段之間的相關性大小不一樣，且各波段反映的光譜特性不同［2］.根據這一特性，為克服不同光譜特性所造成的運算結果相近的問題，則應根據波段之間的相關性(如圖2所示)，采用自適應子空間分解(ASD)算法在相關性極小值點小于閾值處，將一組多維的高光譜數據按波段之間的相關性大小分為若干個獨立的波段子集，然后分別在各個相關性較大的波段子集內進行主成分分析［3］去相關處理.

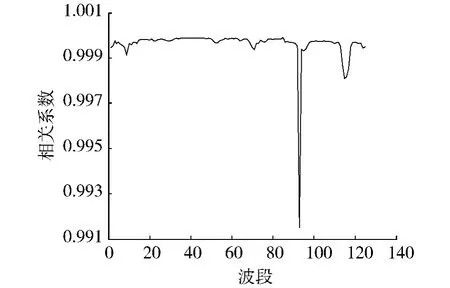
圖2 高光譜圖像相鄰波段之間的相關系數Fig.2 Correlation coefficient of adjacent bands for hyperspectral image

主成分分析是均方差最小意義上的最佳正交變化，亦可以看作是以均方差最小為投影指標的投影尋蹤，在幾何意義上相當于進行空間坐標的旋轉，第一主成分是波譜中數據散布最集中的方向，第二主成分是與第一主成分正交且數據散布次集中的方向，以此類推.它能使變換后產生的新分量正交或者不相關，均方差最小且能量最集中［3］.每一個高光譜圖像都可被看作是一個采樣向量，采樣樣本的數目為原始波段的數目L，即將高光譜圖像數據整理成L×N矩陣X，X=［x1x2…xN］，其中xi代表一個像素點，每一行代表一個波段.估算矩陣X的協方差矩陣C，并將估算的背景協方差矩陣進行特征值分解為

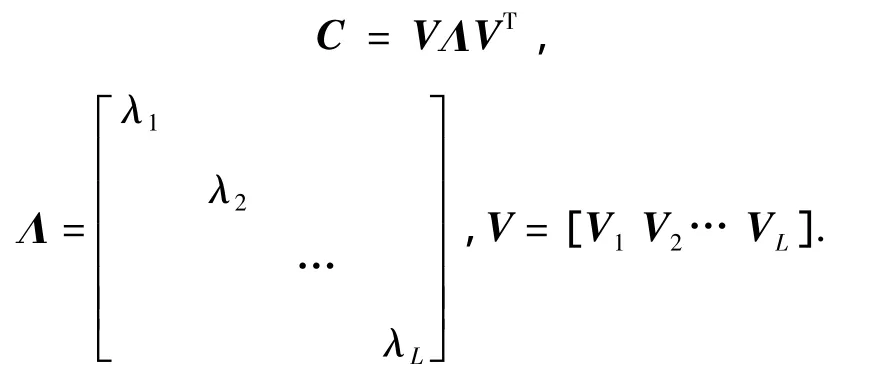
式中:Λ的對角元素為背景協方差矩陣C的非零特征值λi;V為非零特征值所對應的特征向量，由于其特征值是一個對角陣，則其各特征向量之間是相互正交的，或者是不相關的.將采樣數據X投影到特征向量V上，從而得到Y=VT·X，使得新分量之間是正交的或者是不相關的.

利用三階累積量(偏度)和四階累積量(峭度)來衡量每個主成分的非高斯特性.在異常檢測中，若某局部窗口服從高斯分布，則相應的偏度和峭度都為零［4］.如果某局部窗口中包含有異常目標，則高斯分布就會被打破，偏度和峭度的絕對值就會變得很大.根據這一特性，用局部平均奇異度(LAS)［5］來度量各主成分的非高斯特性，即包含異常目標的可能性大小，并用NLAS來標記.實驗中根據圖像的大小適當地選擇窗口的大小，最終采用一個10×10的窗口模板來遍歷每一個主成分.當在某局部窗口內其偏度和峭度均大于設定的閾值時，該主成分的局部平均奇異度NLAS自加1，用這個窗口模板遍歷該主成分，統計該主成分的局部平均奇異度NLAS.所得的NLAS越大，則該主成分的非高斯特性越強，所包含的異常目標信息越多，即選取這樣的主成分用于后續的異常檢測［6］.

1.2 KRX算法

RX算法是應用最為廣泛的一種異常檢測算法，而將原采樣數據通過非線性映射函數映射到高維(可能是無限維)的特征空間中，就形成了核空間中的KRX算法［7-8］，其算子可表示為

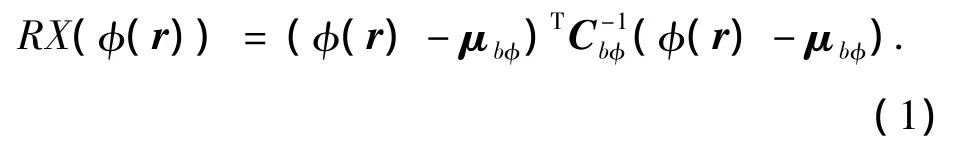
式中:Cbφ和μbφ分別為特征空間中背景協方差矩陣和均值的估計.經過特征值分解后得到核空間RX算法的表達式為

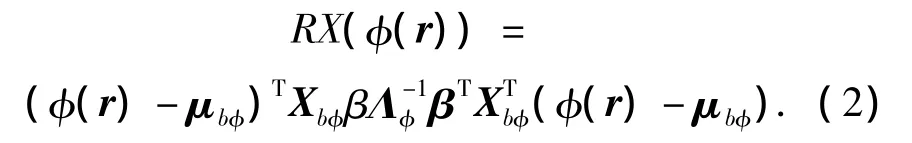
式中:β=［β1β2… βN］T為經過核矩陣K相應特征值的平方根歸一化之后的特征向量.但是由于數據的維數很高(甚至是無限維的)，不能直接通過非線性映射函數φ將原始數據映射到高維特征空間中來實現該算法.為了避免直接計算式(1)，采用核技術［9-10］，用原始數據空間中的核函數來間接地實現高維特征空間中的內積，即由

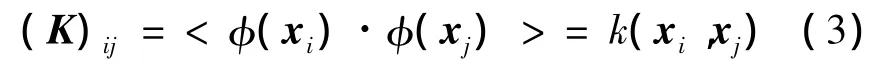
來間接地計算式(2).由文獻［5-6］和KPCA［8］得到KRX算法最后的檢測算子為

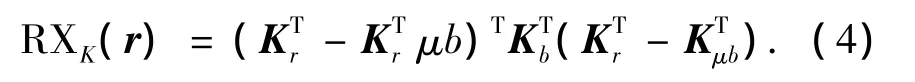
式中:

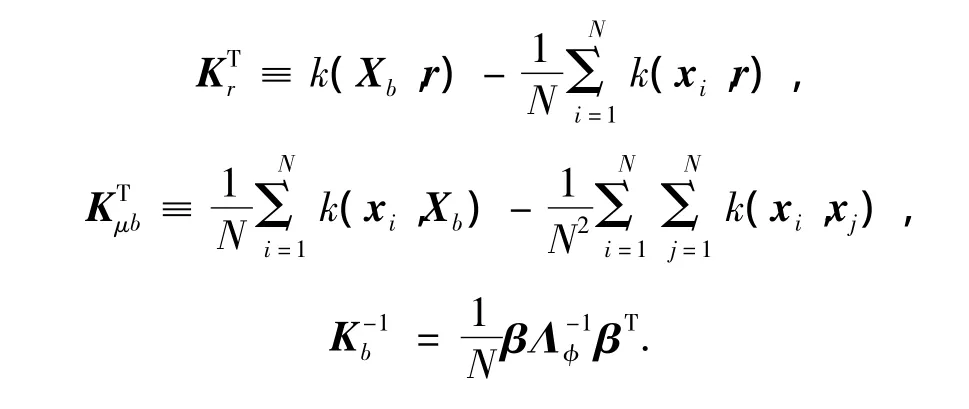
2 仿真結果及其分析

2.1 數據描述

為驗證本文提出的異常檢測算法的有效性，筆者利用AVIRIS高光譜數據源進行了仿真實驗.該圖像覆蓋了從可見光到短波紅外的光譜范圍，除去水的吸收帶和信噪比較低的波段后，余下的126個波段參與仿真實驗.所用實驗圖像大小為100× 100，該圖中包含了38個異常小目標.所用實驗圖像的第10個波段以及地面目標分布如圖3、4所示.

圖3 第10波段Fig.3 The tenth band

圖4 地面目標分布圖Fig.4 Ground target distribution

2.2 實驗結果與分析

在實驗中，首先對數據進行歸一化處理，之后計算相鄰波段之間的相關性，根據相關性的大小從相關性值的極小值點小于設定的閾值處將高光譜圖像分為5個波段子集，波段子集1為第1－8波段，波段子集2為第9－70波段，波段子集3為第71－94波段，波段子集4為第95－114波段，波段子集5為96－126波段.在每一個波段子集上進行主成分分析，消除波段之間的相關性，選取局部平均奇異度最大的波段，綜合起來作為最終用于KRX異常檢測的數據源.

圖5 SSPCAFig.5 SSPCA

在進行KRX算法檢測時，采用局部同心雙窗口，其中外窗為背景檢測窗，用來計算背景特性，內窗為目標檢測窗，中心點為待檢測像素點，并根據圖像的大小和空間分辨率，將背景檢測窗口大小定為11×11像素，目標檢測窗口大小定為3×3像素.對于核函數的選擇，本文采用徑向基核函數，在核函數選擇之后其參數的確定是及其重要的，這是因為參數合適選取可使得數據體現所需要的非線性特性.本實驗中需要確定的參數為徑向基核函數的寬度σ，由于最優參數的選擇還沒有完善的指導理論，因此文中的參數是通過大量的實驗仿真比較其結果最終確定的，本文將徑向基核函數的寬度σ定為0.07.

在利用式(4)得到各像素點對應的檢測值之后，由于目標都是孤立和較小的，因此采用形態學方法提取出像素點較少的目標區域.利用本文提出的算法(SSPCA)檢測最終得到的二值圖像如圖5所示.為了便于分析比較，試驗中還對原始數據直接進行KRX算法和綜合各波段子集中能量最大的波段(記為SMIPCA)用于KRX檢測進行了仿真，并進行形態學處理.在相同閾值下其檢測效果分別如圖6、圖7所示.

圖6 KRXFig.6 KRX

從圖5、6的比較可以看出，本文提出算法的檢測性能明顯優于其他2種.這是因為直接將KRX算法用于原始高光譜圖像，忽略了波段之間的高度相關性，從而產生了較多的虛警.而圖7所示檢測結果不理想是因為能量最大主成分中包含的異常目標信息相對于局部平均奇異度最大波段要小得多，甚至包含的很少，其主要包含的是背景能量信息.因而，在相同的檢測閾值下，本文提出算法有明顯的優勢，證明了算法的有效性.

圖7 SMIPCAFig.7 SMIPCA

為了更具體地說明本文提出算法的優越性，以高光譜圖像檢測到的目標個數、目標所占像素數、虛警所占像素數以及計算時間(單位為s)為指標對上述仿真結果進行比較，其比較結果如表1所示.

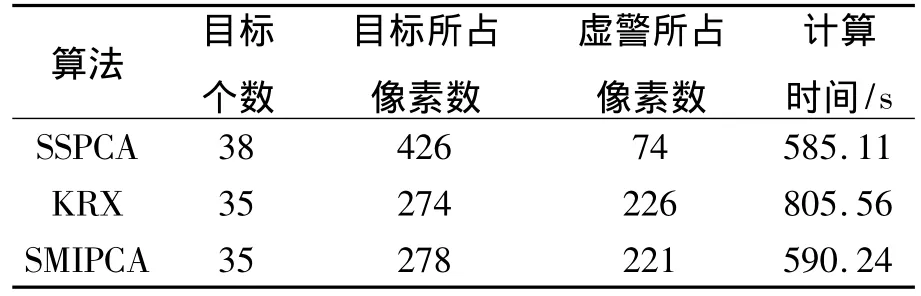
表1 算法性能比較Table 1 Algorithm performance comparison

從表格的數據中可明顯看出，本文提出的算法可檢測到較多的目標，具有較高的目標檢測率和較低的虛警率，且節省了計算所用的時間，充分說明了本文算法的優越性能.

算法特性曲線用于描述不同檢測閾值下檢測概率Pd與虛警概率Pf之間的變化關系，提供算法檢測性能的定量分析.將檢測概率Pd定義為檢測到的真實目標像素數目與地面真實目標像素數目的比值;虛警概率Pf定義為檢測到的虛警像素數目同整幅圖像像素數目總和的比值.通過考察檢測到的異常點是否落入真實目標分布模板區域來判定檢測到的是真實目標還是虛警.上述3種算法的特性曲線如圖8所示，從圖中可以看出本文提出算法較好地改進了KRX算法，具有良好的檢測性能和較低的虛警率.

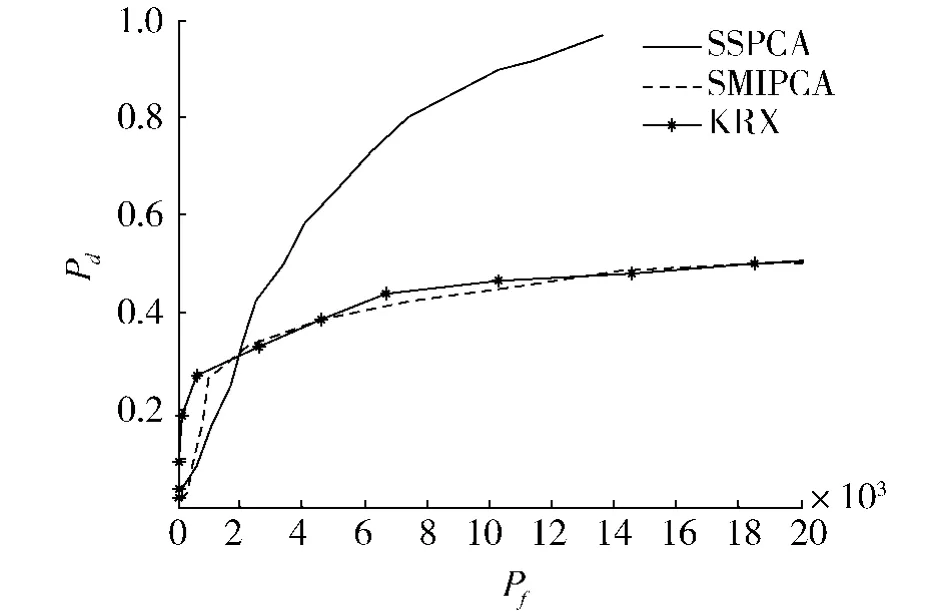
圖8 算法特性曲線Fig.8 Algorithm characteristics curves

3 結束語

本文提出了一種基于選擇性分段主成分分析與KRX算法相結合的異常目標檢測算法.該算法充分利用了各波段子集內部較高的相關性，在有效降低數據維數的同時盡可能地保留了異常目標信息，并充分挖掘了數據的高階統計信息，運用KRX算法對目標進行檢測，達到了比較好的異常檢測效果.

［1］童慶禧，張兵，鄭蘭芬.高光譜遙感——原理、技術與應用［M］.北京:高等教育出版社，2006:218-237.

［2］賀霖，潘泉，趙永強.基于波段子集特征融合的高光譜圖像異常檢測［J］.光子學報，2005，34(11):1752-1755.

HE Lin，PAN Quan，ZHAO Yongqiang.Anomaly detection based on feature fusion of band subset for hyperspectral image［J］.Acta Photonica Sinica，2005，34(11):1752-1755.

［3］張媛，何明一，梅少輝.基于主分量和獨立成分分析的多光譜目標檢測［J］.遙感技術與應用，2006，21(3):227-231.

ZHANG Yuan，HE Mingyi，MEI Shaohui.Target detection of multi-spectral image based on PCA and ICA［J］.Remote Sensing Technology and Application，2006，21(3):227-231.

［4］梅鋒，趙春暉.基于空域濾波的核RX高光譜圖像異常檢測算法［J］.哈爾濱工程大學學報，2009，30(6):697-720.

MEI Feng，ZHAO Chunhui.Spatial filter based anomaly detection algorithm for hyperspectral imagery kernel RX detectors［J］.Journal of Harbin Engineering University，2009，30(6):697-720.

［5］GU Yanfeng，LIU Ying，ZHANG Ye.A selective kernel PCA algorithm for anomaly detection in hyperspectral imagery［J］.IEEE Trans Geosci Remote Sensing，2006，2(10): 725-728.

［6］趙春暉，王楠楠.基于背景抑制及頂點成分分析的高光譜異常小目標檢測［J］.應用科技，2009，36(9):11-14.

ZHAO Chunhui，WANG Nannan.Anomaly detection of hyperspectral imagery based on background restrain and VCA［J］.Applied Science and Technology，2009，36(9):11-14.

［7］KWON H，NASRABADI N M.Hyperspectral anomaly detection using kernel RX-algorithm［C］//2004 International Conference on Iamge Processing.Singapore，2004:3331-3334.

［8］KWON H，NASRABADI N M.Kernel RX-algorithm:a nonlinear anomaly detector for hyperspectral imagery［J］.IEEE Trans Geosci Remote Sensing，2005，43(2):388-397.

［9］SCHOLKOPF B，SMOLA A J.Learning with kernels［M］.Cambridge:The MIT Press，2002:1-21.

［10］SCHOLKOPF B，SMOLA A J，MULLER D R.Kernel principal component analysis［J］.Neural Computation，1999，24(10):1299-131.