巖體結構面模擬方法探析

韓春秀,胡英,施繼余

(昆明冶金高等專科學校建筑工程學院,云南昆明650033)

國際巖石力學學會將巖體中的斷層、軟弱層面、大多數節理、軟弱片理和軟弱帶等各種力學作用形成的破裂面和破裂帶定義為結構面(Discontinuity)。據統計,全球350座水庫壩址區的基巖滑坡,有50%以上的岸坡失穩是因巖體結構面的影響而引發的。因此,準確認識和描述結構面特性對研究巖體的工程穩定性具有重要意義。由于結構面的復雜性,關于巖體中結構面的模擬,仍是至今未能得到妥善解決的一個重要問題。

1 巖體結構面的模擬技術

目前對巖體結構面進行模擬的方法有兩種,一種是為獲得表征結構面幾何關系的網絡模擬,另一種是為獲得表征結構面力學特征的數值模擬。筆者認為只采用一種方法進行是不合適的,因為不同類型的結構面所表現的形態、大小、特征等方面都存在差異,所以首先應對結構面進行分類,再有針對性地采取不同方法進行模擬分析。

1.1 結構面的分類

結構面按其是否可由地質調查完全確定分為確定性結構面和隨機性結構面。確定性結構面(工程分級為Ⅰ、Ⅱ級的結構面)通常是指發育規模較大的結構面,這種結構面近似連續,有確定的延伸方向,延伸長度為數十米至數百米不等,可有一定的厚度或影響帶。如：斷層面或斷層破碎帶、軟弱夾層、長大緩裂隙,長大裂密帶,貫通性結構面等。

隨機結構面(工程分級為Ⅲ級的結構面)指大量隨機分布于巖體中的短小節理,這類結構面屬于硬性結構面,它們隨機斷續分布,延伸長度為米級至十幾米,具有統計優勢方向,主要是各類原生裂隙和構造裂隙。

1.2 巖體結構面的模擬方法分析

確定性結構面構成巖體力學作用邊界,控制巖體變形破壞的演化方向,對巖體穩定性具有很大的控制意義,主要通過數值模擬進行分析。就目前模擬技術來說,無論是有限元、邊界元、離散元、還是它們的耦合計算,以及它們與模糊數學、概率統計、分形幾何或損傷力學、斷裂力學的結合等等,其計算結果的可靠性均取決于巖體結構模型的正確與否以及結構面的參數選取。

隨機結構面的分布具有隨機性、形態多樣、分布不均勻和空間組合的復雜性,所以很難表征結構面的分布。目前在這方面的工作主要遵循兩條途徑：(1)統計模型方法。(2)概率模型方法。第一種方法往往需要大量的現場調查和測量,受測量露頭限制的影響較大,而第二種方法對巖體結構的描述較為籠統,不夠具體。實際上結構面在巖體的分布既具有隨機的一面,也有其確定性的一面,應該結合這兩種方法進行分析。

筆者認為應綜合考慮現場調查測量的局限性,充分利用統計、概率模型的優勢以及數值模擬技術,從綜合的角度探討結構面的模擬技術。具體做法是：把模型看成是一個等效連續復合體,先針對短小、非貫通的隨機結構面,采用蒙特卡洛方法對其進行網絡模擬,以獲得這些結構面的傾角、跡長等幾何特征,并計算出力學參數;再利用Ansys模擬技術對規模較大的確定性結構面進行數值模擬,按非均質體處理,同時看成宏觀的連續體,隨機結構面對模型的影響在巖體參數選擇中考慮,而不是在模型的尺寸上考慮。

2 工程應用分析

鹽津橋水庫位于貴州省仁懷市境內,是一個以灌溉、發電、供水及旅游為目的的綜合水利工程。壩址河床高程為569m,正常水位高650m。右岸壩肩下游為復式谷坡,地形為陡崖,地形坡角70°～80°,為斜向坡,相對高差約124m。597～660m高程內距壩端下游20～50m左右巖體為臨空面。邊坡坡體出露地層為寒武系中上統婁山關群第二段的淺灰至灰色中厚層夾薄層含硅質粉、細晶白云巖、砂屑白云巖及薄層泥質白云巖,白云巖偶夾軟弱夾層。第四系主要由殘、坡積堆積的亞粘土夾塊石、碎石和石灰石組成,厚約0.5～1.0m。由于壩肩巖體為順層邊坡,再加上裂隙發育,嚴重影響壩肩的穩定性。

2.1 隨機結構面的蒙特卡洛模擬

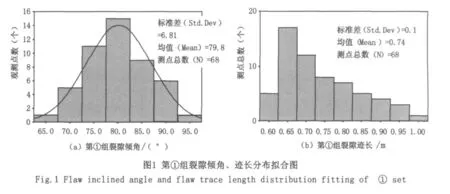
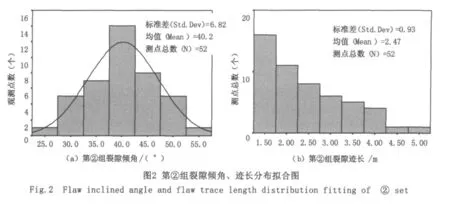
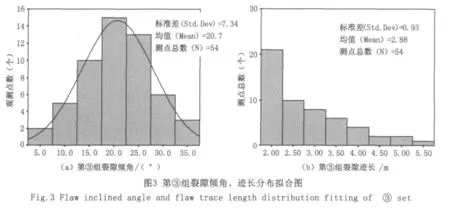
隨機結構面的統計模型：在右壩肩下游處,首先由測網數據統計出裂隙的優勢方位,確定出三組裂隙組,其產狀為：①N72°E/80°NW、②N23°E/40° SE及③N33°W/20°NE。采用統計軟件SPSS分別對三組裂隙進行傾角分布擬合(圖1(a)、圖2(a)、圖3(a)),通過假設檢驗得到,樣本中三組裂隙的傾角均服從正態分布;對各組的裂隙跡長進行分布擬合(圖1(b)、圖2(b)、圖3(b)),得到第①組樣本的裂隙跡長服從對數正態分布,第②、③樣本的裂隙跡長服從負指數分布。

隨機結構面的概率模型。上節中計算的跡長屬于測線跡長,而我們需要的是總體跡長,總體跡長取測線跡長時的概率有多大呢?跡長的分布情況不同,兩者參數的轉換結果也不一樣,表1列出的是Priest和Hudson推導出的全跡長與測線交切跡長參數的轉換關系。從而可算出三組裂隙的總體跡長均值分別為μL1=0.56m(μL+0.12/μL=0.74),μL2=2.47/2=1. 235m,μL3=2.88/2=1.44m。

表1 各種跡長分布的均值轉換(據Priest和Hudson,1981)Tab.1 Transformation of typical value for all kinds of distributed trace lengths (Base on Priest and Hudson,1981)

隨機結構面的蒙特卡洛模擬。采用Monte-Carlo方法,在右岸下游研究區進行裂隙網絡的模擬,二維裂隙網絡是由不同長短、不同傾角的裂隙形成的圖形(圖4)。該圖從直觀上描述了隨機裂隙的幾何分布,分布的結果可用于推求巖體的綜合統計力學參數。論文在進行數值模擬時,計算復合模型力學參數就用到該成果。

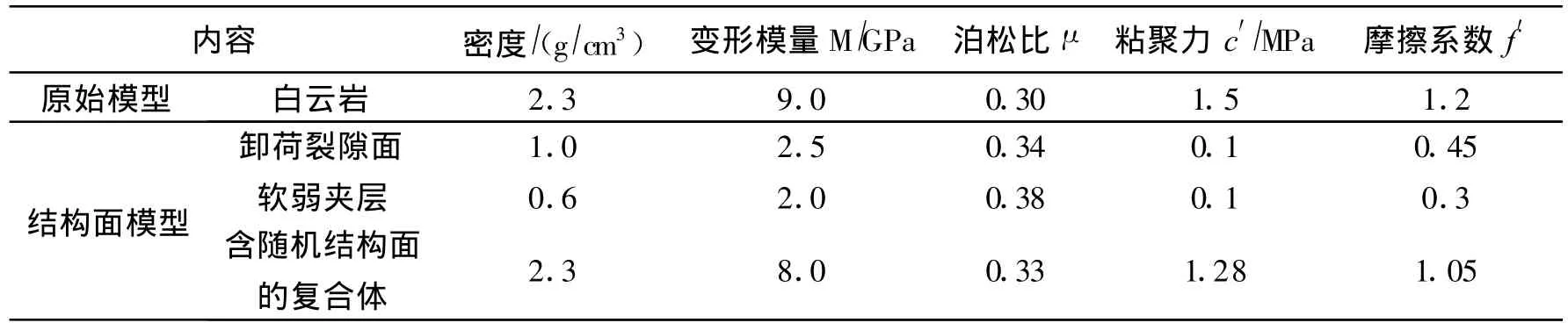
表2 計算模型各材料力學參數選用表Tab.2 All kinds of parameters of mechanics of materials in computation module

2.2 確定性結構面的數值模擬

結構面的參數選取：巖體的參數確定一直是巖土工程中的一個重要及困難的問題,巖體力學參數的合理取值,是計算機模擬結果合理的關鍵。根據結構面的規模情況,本論文中巖體材料力學參數的選取分兩部分：一是完整巖塊、卸荷裂隙、軟弱夾層及隨機裂隙的力學參數均參考水利水電勘測設計研究院提供的地質資料以及相關巖石室內試驗資料。二是含隨機結構面的力學參數采用等效連續復合模型,通過理論計算獲得(表2)。

其它計算要素說明：采用有限元軟件ANSYS進行模擬,為了研究巖體的某些特定的性質(例如結構面變形的影響程度),忽略了一些次要的因素(例如巖石內部的一些微觀缺陷),而著眼于巖體的最主要的性質。因此,論文在模擬時進行以下假設：力學模型為宏觀連續體,本構關系采用彈塑性模型;不考慮巖石內部微觀孔洞等缺陷的影響;結構面是平滑的,不考慮粗糙度的影響;結構面兩側巖體的變形為小變形;巖體的屈服破壞符合德魯克-普拉格準則;結構面模型如圖5。

3 結論

1)采用蒙特卡洛(Monte-Carlo)方法可以對結構面進行由局部到整體、由表及里的模擬,能在統計意義上了解在一般情況下難以觀察、測量到的巖體內部結構面的發育情況。

2)此方法有效解決了無法對數量多、尺寸小的節理進行逐條模擬的問題,又從變形和強度的弱化方面把節理考慮進去,與現實情況近似,是一種行之有效的方法。

[1]黃潤秋.復雜巖體結構精細描述及其工程應用[M].北京：科學出版社,2004.

[2]魏云杰.金沙江白鶴灘水電站巖體結構及其對壩肩抗滑穩定性的控制作用[D].成都：成都理工大學,2004.

[3]張有天.巖石水力學與工程[M].北京：中國水利水電出版社,2005.

[4]博弈創作室.ANSYS7.0基礎教程與實例詳解[M].北京：中國水利水電出版社,2004.

[5]小颯工作室.最新經典ANSYS及Workbench教程[M].北京：電子工業出版社,2004.

[6]龔曙光.ANSYS操作命令與參數化編程[M].北京：機械工業出版社,2004.

[7]趙建鋒.巖體弱面的分形性與含弱面巖體破壞的力學行為研究[D].遼寧：遼寧工程技術大學,2001.

[8]李達仕.巖體結構面網絡模擬及工程應用研究[J].工程技術,2009(12)：60-60.

[9]徐衛亞,楊圣奇.節理巖石剪切流變特性試驗與模型研究[J].巖石力學與工程學報,2005,26(6)：1323-1236.

[10]沈明榮,張清照.規則齒型結構面剪切特性的模型試驗研究[J].巖石力學與工程學報,2009,29(4)：713-719.

[11]陳新朝,李斌,張永央.盤石水庫右壩頭巖體結構面工程特性淺析[J].山西建筑,2009,35(23)：127-129.

[12]楊錫祥,周英芳,趙小稚.蠶莊金礦上莊礦區巖體結構面分析及應用[J].黃金,2010(2)：27-30.

[13]方俊彥.邊坡巖體結構面特征[J].研究科學與管理, 2010(4)：95-96.