無線傳感器網絡延時測量數據的信息熵與不確定性

王 婕

（中北大學電子與計算機科學技術學院，太原 030051）

0 引言

無線傳感器網（wireless senser network，WSN）由大量傳感器節點組成，傳感器節點負責對監測區域內的某些特定數據進行采集，并通過無線通信方式形成的一個多跳自組織網絡，是一種新的分布式系統。WSN能夠檢測、監控和處理現實生活中的很多問題，在軍事上實現戰場的實時監控，對森林火災和動物棲息地的監控口，在醫學上監護病人的病情等都有很好的應用。

WSN是一個以數據為中心的網絡，通常具有數據融合功能的網關節點會收集普通節點發送給它的原始信息，然后對信息進行分析和處理。為了保持節點本地時間的一致性，必須調整本地時鐘。時間同步協議為精確地調整本地時鐘提供了依據。

目前許多科學家和工程技術人員對無線傳感器網絡時鐘同步進行研究，并取得了很好的成果，概括起來大致分為3類[1]：

（1）基于發送者和接收者的單向機制

在這個機制中，發送節點廣播含有節點本地時間的分組，廣播范圍內的節點測量分組的傳輸延遲，再根據接收到的分組中包含的時間，即可得到與發送者間的偏差，進而同步。典型的算法如FTSP算法和由伯克利英特爾研究實驗室提出的延時測量時間同步協議（DMTS）算法。

（2）基于發送者和接收者的雙向機制

這種機制類似于Internet上的NTP協議，典型的算法如TPSN算法。

（3）基于接收者和接收者的機制

這種機制利用無線數據鏈路層的廣播信道特性，引入第三方節點廣播一個參考分組，在廣播域內的接收節點收到這個分組后，通過比較各自接收到消息的本地時間，即可得到接收者間的偏差，如RBS算法。

本文在 DMTS算法基礎上結合時延的指數分布特性，建立了相應的模型，然后又用最大熵方法的網絡延遲概率密度函數，結合不確定度對其函數進行評價，使得根據最大熵原理計算的概率密度函數更接近于真實值。

1 傳感器網絡時鐘同步原理

傳感器網絡中節點的本地時鐘依靠對自身晶振中斷計數實現，晶振的頻率誤差和初始計時時刻不同，使得節點之間的本地時鐘不同步。如果能估算出本地時鐘與物理時鐘的關系或者本地時鐘之間的關系，就可以構造對應的邏輯時鐘以達成同步。

節點時鐘通常用晶體振蕩器脈沖來度量，所以任一節點i在物理時刻t的本地時鐘讀數可表示為[2]：

其中t為真實物理世界的時間；f0為節點晶振的標稱頻率；f(t)為晶振的實際頻率；t0代表開始計時的時刻；Ci(t0)為計時開始t0的時鐘讀數。

對任何兩個時鐘A和B，分別用CA(t)和CB(t)來表示它們在t時刻的時間值，那么[3]：

偏移可表示為：CA(t)—CB(t)

2 DMTS算法

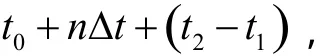
然而我們用公式 t0+nΔ t + (t2? t1)調整時鐘是有誤差的，而這個時延誤差一般符合指數分布。DMTS協議的精確性要取決于延時測量的精確度，它是一種靈活輕量級能量，利用高效的時鐘同步機制可應用于時鐘同步要求不太高的無線傳感網絡中，該機制還能夠更好地支持與外部時鐘源及多跳點的同步。

3 模型的建立

由DMTS算法，不難得到：

化簡得：

圖1 DMTS時鐘同步算法

其中 表示接收方與發送方的時鐘偏移量，nΔ t表示傳輸時延的固定部分，X表示時延的可變部分。

文獻[5-7]不但證明了指數分布對隨機時延是正確的，而且還提出了幾種估計時鐘偏移量的算法。這都證明了假設隨機延遲服從指數分布是正確的。

令Y= (t1?t0)， z = n Δ t +，X=Y?z，因為X服從均值為 的指數分布，它的密度函數為：

最大熵原理[1-2]是在1957年由E.T.Jaynes提出的，其主要思想是，在提供數據有限或概率空間不完備的情況下，估計概率分布或確定未知參數，應充分利用現有信息，選擇出具有信息熵最大的那一種概率分布，作為估計或預測的結果。

運用最大熵原理附加其約束條件和屬性條件：

基于最大熵原理，對信息熵函數附加的（3）和（4）約束條件和屬性條件，借助拉格朗日乘子法，推導出對數正態分布隨機變量所服從的最大熵分布公式。

M對 f ( x)求偏導，并使其等于0得：

所以滿足上述3個約束條件的最大熵分布的概率密度函數為：

4 時鐘同步測量結果的不確定性分析

報文傳輸延遲的不確定性是無線傳感器網絡時鐘同步的挑戰之一。 一方面傳輸延遲比要求的時間同步允許的誤差大得多，另一方面它極易受到處理器負載、網絡負載等因素的影響。通常，報文的傳輸延遲可分為：發送延遲、訪問時間延遲、傳輸時間延遲、傳播時間延遲、接收時間延遲、接收處理時間延遲。傳輸延遲的不確定性嚴重影響了同步精度，因此需要對傳輸延遲仔細的測量、分析和補償才能設計出高精度的時間同步協議。

我們用仿真實驗的方法再來驗證模型，根據DMTS算法對無線傳感器時鐘的測量，為方便計算，在確定的[0ms，4ms]區間內，取出300個樣本如圖2所示，經過計算得0= 0 . 3 4 1 和1= ? 1 . 4 2 8 ，最大熵分布的概率密度函數分布圖如圖3所示。

圖2 原始數據

圖3 概率密度函數分布圖

根據不確定度的評定如下[10]：

用本文采用的方法所估計的測量結果及其不確定度，比較接近于指數分布的被測量理論真值0.7和理論不確定度0.7，符合模型的結論。

5 結束語

本文主要利用時鐘偏移量誤差的規律性，提出基于指數時延的無線傳感器網絡時鐘同步估計算法。基于發送者同步模型，在DMTS算法的基礎上引入指數時延得到的。針對無線傳感器網絡延遲測量數據處理中摻雜的主觀因素不能準確反映客觀現實的問題，采用最大熵方法，根據測量數據求取被測量的概率分布，進而結合不確定度對此概率分布在約束條件下進行估計和評價。

[1] 楊博，廖明宏.基于統計的無線傳感器網絡時鐘同步協議[J].哈爾濱工業大學學報,2007,39（1）:98-100.

[2] 陳橋.無線傳感器網絡的時鐘同步算法的研究與應用[D].西安:西安理工大學,2010:11-12.

[3] 劉曉璐，周書民.無線傳感器網時間同步算法的比較[J].江西科學,2010,28（4）:521-523.

[4] 程麗娟.無線傳感器網絡時間同步算法研究[D].西安:西北工業大學,2007:26-27.

[5] Jeske DR.On maximum-likelihood estimation of clock offset[J].IEEE Transactions on Communications，2005,53(1)：53-54.

[6] Qasim M Chaudhari,Erchin Serpedin.Clock estimation for longterm synchronization in wireless sensor networks with exponential delays[J].EURASIP Journal on Advances in Signal Prossiong,2008,(1):1-6.

[7] 田賢忠,龔婷.基于指數時延的無線傳感器網絡時鐘同步估計[J].小型微型計算機系 統,2009,11:2186-2188.

[8] 田寶玉,楊潔.信息論基礎[M].北京:人民郵電出版社,2008:255-273.

[9] 凌能祥.信息熵在復雜性供應鏈協調中的應用[D].合肥:合肥工業大學,2007:20-24.

[10] 程亮,童玲.最大熵原理在測量數據處理中的應用[J].電子測量與儀器學報,2009,23(1):47-50.