一種新型SMA阻尼器及其減震性能*

凌育洪 彭輝鴻 張帥

(1.華南理工大學建筑設計研究院，廣東廣州510640;2.華南理工大學土木工程系，廣東廣州510640)

形狀記憶合金(簡稱SMA)是一種被廣泛研究的新型功能材料［1-2］.近20年來，國內外眾多學者對SMA的力學性能進行了深入的研究，并設計出了多種類型的被動阻尼裝置，發現SMA阻尼裝置在建筑結構耗能減震方面具有很好的適用性.文獻［3-4］中研究了SMA絲的力學性能，結果表明SMA絲不僅具有良好的耗能能力，而且在經歷多次滯回變形后，殘余變形幾乎為零.Dolce等［5］設計了一種具有自復位能力的阻尼器，試驗結果表明該阻尼器具有初始剛度大、自復位和耗能能力強、構造簡單的特點;Zhang等［6］采用超彈性NiTi鉸線設計了一種可重復使用的遲滯阻尼器(RHD);Wilde等［7］采用SMA設計了一種用于高架橋梁的隔震裝置;Li等［8］利用SMA超彈性開發了兩種新型的SMA阻尼器——拉伸型SMA阻尼器和剪刀型SMA阻尼器，并對安裝了該阻尼器的五層鋼框架模型進行了振動臺試驗，發現兩種阻尼器均能有效降低結構的位移響應;Zuo等［9］提出了一種SMA復合摩擦阻尼器;陳海泉等［10］提出了一種SMA橡膠支座;此外，倪立峰、薛素鐸等［11-12］也相繼提出了不同形式的SMA阻尼器.

文中采用國產超彈性NiTi絲設計了一種新型SMA自復位阻尼器，該阻尼器構造簡單且便于安裝.文中首先介紹了NiTi絲的材性試驗結果，根據Brinson一維本構模型模擬了該種NiTi絲的相變超彈性;隨后詳細介紹了一種新型SMA阻尼器的構造與工作原理，并對阻尼器的滯回模型進行了數值模擬;最后對裝有該阻尼器的一層鋼框架模型進行動力時程分析，驗證該SMA阻尼器的減震效果.文中主要是通過數值方法研究一種新型SMA阻尼器的力學性能，從而為制作阻尼器及后續阻尼器性能試驗奠定基礎.

1 Brinson本構模型

Brinson本構模型［13］具有很強的工程應用性且便于進行有限元分析，因此在實際工程結構中的應用十分廣泛.它采用非常數材料參數，并將馬氏體含量表示為應力誘發馬氏體含量和溫度誘發馬氏體含量.經積分后，其一維本構方程可寫成下述形式:

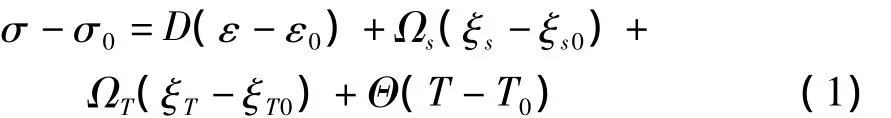
式中:

D、Θ、Ωs分別為彈性模量、熱彈性系數和應力相變系數;ΩT為溫度相變系數，當材料溫度恒定且完全處于奧氏體狀態時，ΩT≡0;DA、DM分別表示奧氏體狀態和馬氏體狀態下的彈性模量;σ、ε分別表示材料的應力和應變;ξs、ξT分別表示應力誘發馬氏體含量和溫度誘發馬氏體含量;T為材料的溫度;εL為形狀記憶合金在相變過程中的最大可恢復應變;式中帶下標“0”的量表示相應變量的初始值.

當材料發生正相變時，即當T＞As且+CM· (T－Ms)＜σ＜+CM(T－Ms)時，材料的相變控制方程為

當材料發生逆相變時，即當T＞Ms且CA(TAf)＜σ＜CA(T－As)時，材料的相變控制方程為

式中，Ms表示馬氏體相變開始溫度，As、Af分別表示奧氏體相變開始溫度和結束溫度，CM、CA分別為馬氏體、奧氏體相變時應力對相變溫度影響程度的材料參數，σcrs、σcrf分別為馬氏體相變開始時和結束時的臨界應力.

2 NiTi絲超彈性簡化模型的建立

首先對一種常溫下處于奧氏體狀態的NiTi絲進行了超彈性性能試驗［14］.NiTi絲由西安賽特有限公司提供，直徑1 mm，組分含量(質量分數)為:Ni 55.8%，Ti 44.2%.經差示掃描量熱儀(DSC)測試測得相變溫度分別為:Mf=－40.8℃，Ms=5.3℃，As=－26.8℃，Af=12.0℃，其中Mf表示馬氏體相變結束溫度.

試驗在華南理工大學土木與交通學院的INSTRON 5567萬能試驗機上進行，主要考慮循環次數、應變幅值和加載速率等參數對NiTi絲超彈性力學性能的影響，試驗溫度為室溫(25℃).試驗中采用等位移加載，力和變形結果由計算機自動采集，應力和應變結果則根據試件直徑及標距換算得到，試件標距為100mm.試驗前，預先對所有試件進行30個加卸載循環以穩定其性能.圖1(a)給出了在加載速率為 0.1 mm/s，應變幅值分別為 0.02、0.03、0.04、0.05、0.06、0.07、0.08時NiTi絲的滯回曲線;圖1(b)給出了在應變幅值為0.06，加載速率分別為0.1、0.5、1.0、2.0mm/s時NiTi絲的滯回曲線.

圖1 不同應變幅值和加載速率下NiTi絲的滯回曲線Fig.1 Hysteretic curves of NiTi wire at different strain amplitudes and loading rates

從試驗結果可以看出，該種NiTi絲表現出了良好的超彈性，卸載后，殘余應變幾乎為零.圖1(a)表明，隨著應變幅值的增大，滯回曲線包圍的面積幾乎呈線性增加，說明材料耗能能力受應變幅值的影響非常大;由圖1(b)中可以看出，隨著加載速率的增加，滯回曲線向斜上方發展，滯回環包圍的面積有所減小，但減小幅度不大，說明材料耗能能力受加載速率的影響不大.因此，在實際工程應用中，一般可忽略加載速率的影響.

為了便于理論計算，文中根據Brinson模型，采用Matlab語言編程求解本構方程［15］，模擬了試驗NiTi絲的超彈性應力－應變關系.圖2給出了加載速率為0.1mm/s、應變幅值為0.08時的試驗及模擬結果.從圖中可以看出，模擬結果能夠較好地反應合金絲的相變超彈性，模擬得到的等效剛度比試驗值小0.051，單圈耗能和等效阻尼比分別比試驗值大0.015和0.070，誤差在允許的范圍內，因此可用圖2的模擬曲線進行后續理論分析.

圖2 NiTi絲的超彈性應力－應變關系試驗曲線與Brinson模型模擬結果Fig.2 Superelastic stress-strain test curve and simulated results based on Brinson model of NiTi wire

3 阻尼器的設計及計算模型

3.1 阻尼器的構造與工作原理

文中設計的阻尼器［16］如圖3所示，該阻尼器同時具有耗能和自復位能力，即在地震過程中，阻尼器利用NiTi絲的超彈性滯回特性耗能，并且在地震結束后，阻尼器能夠回復至震前的狀態.

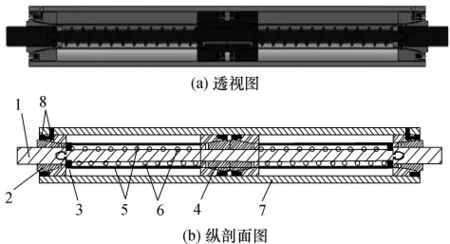
圖3 SMA阻尼器結構圖Fig.3 Construction of SMA damper1—內桿;2—外錨;3—滑動擋板;4—內錨;5—NiTi絲; 6—預壓彈簧;7—外筒;8—螺釘;圖4中與此同

由圖3可以看出，阻尼器由內桿1、外錨2、滑動擋板3、內錨4、預壓彈簧6、外筒7和NiTi絲5組成.內桿1與內錨4焊接在一起，外錨2與外筒7通過螺釘固結;NiTi絲5一端通過擠壓錨具與內錨4連接，另外一端通過擠壓錨具與外錨2連接(將NiTi絲拉伸至超彈性平臺的中間位置后再與錨具連接)，左右兩NiTi絲組構成了阻尼器的耗能組，用于耗散地震能量;預壓彈簧6一端緊靠內錨4，另外一端緊靠滑動擋板3，兩預壓彈簧組構成了阻尼器的復位組，確保地震結束后阻尼器能夠回復至初始狀態.該阻尼器的最大行程取決于NiTi絲的長度以及NiTi絲的應變幅值，因此通過調整這兩個參數可設計出滿足不同設計要求的阻尼器.

阻尼器可以層間支撐的形式安裝于結構層間，例如外筒7通過斜撐與上層框架相連，內桿1通過斜撐與下層框架相連，這樣，層間位移即轉化為內桿與外筒的相對位移.因此，當內桿相對外筒發生相對滑動ΔL時(見圖4(a))，一側合金絲伸長ΔL，而另一側合金絲縮短ΔL，根據內桿的平衡條件有

式中，Fn為伸長絲組和縮短絲組的內力差，F1、F2分別為伸長絲和縮短絲作用于內桿上的力，S0為NiTi絲的截面積，σ1、σ2分別為伸長絲和縮短絲的應力.

當內桿相對外筒發生相對滑動ΔL時，復位組的運動如圖4(b)所示，一側彈簧被壓縮ΔL，另一側彈簧則保持初始狀態不變，因此根據內桿的平衡條件有

圖4 SMA阻尼器工作原理圖Fig.4 Working principle of SMA damper

式中，Fs為復位組產生的回復力，F3為縮短彈簧的恢復力，Fc為彈簧的預壓力，εs為彈簧新狀態下的應變，ks為彈簧剛度.

綜上所述，阻尼器的受力F(即內桿與外筒發生相對位移ΔL時，外界作用在內桿上的力)可表示為

3.2 阻尼器的數值模擬

根據阻尼器的工作原理以及絲材的試驗結果，文中設計了一縮尺阻尼器，其參數如下:外筒長1200mm、外徑50 mm、內徑35 mm;NiTi絲總根數24(每側12根)、直徑1mm、長度500 mm;NiTi絲預應變(即初始應變)0.036、應變幅值0.030;彈簧預壓力2.4kN、剛度0.05MN/m.阻尼器的最大行程為15mm，因此只要阻尼器的行程不大于15mm就可以使NiTi絲在結構振動過程中始終處于拉伸狀態，從而避免了合金絲的受壓屈曲.

若設NiTi絲的預拉伸應變為ε0，預應力為σ0，彈簧預應變εs0，則當阻尼器產生位移ΔL時，伸長絲、縮短絲和彈簧的應變如下:

式中:ε1為伸長絲應變;ε2為縮短絲應變;L0為合金絲和彈簧的初始長度.將新的應變值代入Brinson本構方程(1)中，并與方程(2)或(4)聯立求解出新狀態下伸長絲與縮短絲的應力σ1、σ2，然后將其依次代入公式(7)－(12)，則可求出阻尼器的受力F.

根據文中提出的計算模型，采用Matlab語言編程，計算出阻尼器的力－位移關系.圖5給出了位移幅值分別為±7.5、±10.0、±15.0 mm時的滯回曲線，其中圖5(c)所示為將圖5(a)和5(b)曲線疊加得到的阻尼器的力－位移曲線.從圖中可以看出，耗能組的滯回環比較飽滿，說明所設計的阻尼器具有良好的耗能能力，且具有較大的初始剛度.另外，彈簧的預壓力取為2.4 kN，這樣保證當阻尼器受力卸載至零時，阻尼器的殘余位移為零，即阻尼器具有完全自復位能力.

4 SMA阻尼器減震分析

為了驗證阻尼器的減震性能，文中采用Matlab語言編寫了動力時程分析程序［17-18］，對裝有該阻尼器的單層鋼框架模型進行了減震性能分析，框架模型如圖6所示.結構模型參數為:k=1×106N/m， m=3000kg，c=0.阻尼器的外筒與內桿通過斜撐分別與鋼框架頂部和底部連接，因此，樓層的相對位移即完全轉化為阻尼器的行程.

圖5 阻尼器滯回曲線Fig.5 Hysteretic curves of damper

圖6 鋼框架模型示意圖Fig.6 Sketch of steel structural model

動力時程分析程序編寫的思路如下:結構動力方程式可表示為

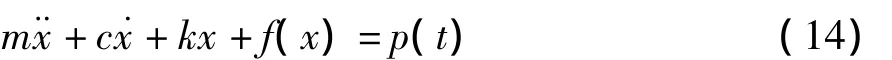
式中:m、c、k分別為結構質量、阻尼與剛度;p(t)為外荷載;f(x)為阻尼器單元提供的回復力，可表示為

式中:kd為阻尼器單元的瞬時切線剛度;fd為阻尼器滯回曲線在豎軸上的截距.將其代入式(14)可得

式(16)可采用Newmark-β法求解，從圖5(a)中可看出，當阻尼器單元的狀態跨越拐點時，其瞬時剛度kd和截距fd都將發生變化，因此需要進行迭代求解，文中采用了Newton-Raphson迭代法，為了簡化編程，程序忽略了鋼框架剛度k的退化，程序流程如圖7所示.SMA阻尼器特征參數如下:初始剛度k0d=1.2×106N/m，屈服后剛度k1d=6×104N/m，屈服力Fdy=2600N，屈服位移Δdy=2.17mm.

圖7 程序流程圖Fig.7 Flowchart of program

地震波采用了Elcentro(NS)波，加速度峰值為3.417m/s2，時間步長0.02s，持續時間8s.經計算得到結構的位移和加速度響應時程曲線如圖8所示.從圖中可以看出，阻尼器對結構的位移與加速度均有控制作用，但對位移的控制更加明顯，無控結構的位移峰值為26.0mm，有控結構的位移峰值為12.5mm，若定義減震率

式中，X0為未安裝阻尼器的原結構(無控結構)振動反應，X1為安裝有阻尼器的結構(有控結構)的振動反應，則由此可知減震率達52%.無控結構的加速度峰值為8.3m/s2，有控結構的加速度峰值為7.2m/s2，減震率為13.3%.由此可見，文中提出的阻尼器具有良好的減震性能，但對加速度的控制效果稍差.最后，通過提取阻尼器的行程及對應的恢復力可得阻尼器的恢復力曲線，如圖9所示.可見文中編制的程序能夠很好地模擬阻尼器的力學性能.

圖8 位移與加速度響應時程曲線Fig.8 Time history response curves of displacement and acceleration

圖9 SMA阻尼器耗能組恢復力曲線Fig.9 Restoring force curves for energy dissipation group of SMA damper

5 結語

文中在對一種國產形狀記憶合金絲力學性能進行試驗研究的基礎上，設計了一種新型的SMA阻尼器，介紹了它的構造與工作原理，通過編程計算得出了阻尼器的滯回模型，用時程分析法比較了安裝和未安裝阻尼器結構的響應，驗證了文中所提出的阻尼器的減震性能.研究發現:(1)由于設置了預壓彈簧，因此阻尼器具有較大的初始剛度和良好的自復位能力;(2)該SMA阻尼器對結構在地震作用下的位移響應具有很好的控制效果，但對加速度的控制效果不顯著.阻尼器模型的制作和試驗驗證還有待進一步探討.

［1］ 崔迪，李宏男，宋鋼兵.形狀記憶合金在土木工程中的研究與應用進展［J］.防災減災工程學報，2005，25 (1):86-94.Cui Di，Li Hong-nan，Song Gang-bing.Progress on study and application of shape memory alloy in civil engineering［J］.Journal of Disaster Prevention and Mitigation Engineering，2005，25(1):86-94.

［2］ Song G，Ma N，Li H N.Applications of shape memory alloys in civil structures［J］.Engineering Structures，2006，28:1266-1274.

［3］ Dolce M，Cardone D.Mechanical behavior of shape memory alloys for seismic applications:austenite NiTi wires subjected to tension［J］.International Journal of Mechanical Sciences，2001，43:2657-2677.

［4］ 李廣波，崔迪，洪樹蒙.超彈性形狀記憶合金絲力學性能試驗研究［J］.大連大學學報，2008，29(3):129-133.Li Guang-bo，Cui Di，Hong Shu-meng.Experimental investigation on mechanical properties of new form superelastic shape memory alloy wires［J］.Journal of Dalian University，2008，29(3):129-133.

［5］ Dolce M，Cardone D，Marnetto R.Implementation and testing of passive control devices based on shape memory alloys［J］.Earthquake Engineering and Structural Dynamics，2000，29:945-968.

［6］ Zhang Y，Zhu S.A shape memory alloy-based reusable hysteretic damper for seismic hazard mitigation［J］.Smart Materials and Structures，2007，16:1603-1613.

［7］ Wilde K，Gardoni P，Fujino Y.Base isolation system with shape memory alloy device for elevated highway bridges［J］.Engineering Structures，2000，22:222-229.

［8］ Li Hui，Mao Chen-xi，Qu Jin-ping.Experimental and theoretical study on two types of shape memory alloy devices［J］.Earthquake Engineering and Structural Dynamics，2008，37:407-426.

［9］ Zuo Xiao-bao，Chang Wei，Li Ai-qun，et al.Design and experimental investigation of a superelastic SMA damper［J］.Materials Science and Engineering:A，2006，438/ 439/440:1150-1153.

［10］ 陳海泉，李忠獻，李延濤.應用形狀記憶合金的高層建筑結構智能隔震［J］.天津大學學報，2002，35 (6):761-765.Chen Hai-quan，Li Zhong-xian，Li Yan-tao.Intelligent isolation of high-rise building structures applying shape memory alloy［J］.Journal of Tianjin University，2002，35(6):761-765.

［11］ 倪立峰，李秋勝，李愛群.新型形狀記憶合金阻尼器的試驗研究［J］.地震工程與工程振動，2002，22 (3):145-148.Ni Li-feng，Li Qiu-sheng，Li Ai-qun.Investigation and experiment of damper based on shape memory alloy (SMA)［J］.Earthquake Engineering and Engineering Vibration，2002，22(3):145-148.

［12］ 薛素鐸，董軍輝，卞曉芳，等.一種新型形狀記憶合金阻尼器［J］.建筑結構學報，2005，26(3):45-50.Xue Su-duo，Dong Jun-hui，Bian Xiao-fang，et al.A new type of shape memory alloy damper［J］.Journal of Building Structures，2005，26(3):45-50.

［13］ Brinson L C.One dimensional constitutive behavior of shape memory alloy:thermomechanical derivation with non-constant material functions and redefined martensite and internal variable［J］.Journal of Intelligent Material Systems and Structures，1993，4:229-242.

［14］ 凌育洪，彭輝鴻，張帥.超彈性NiTi絲力學性能試驗研究［J］.華南理工大學學報:自然科學版，2010，38 (4):131-135.Ling Yu-hong，Peng Hui-hong，Zhang Shuai.Mechanical behavior of superelastic NiTi wires［J］.Journal of South China University of Technology:Natural Science Edition，2010，38(4):131-135.

［15］ 樊劍，彭剛，龍曉鴻.復雜應力狀態下SMA熱力學方程的求解［J］.華中科技大學學報:自然科學版，2003，31(9):22-24.Fan Jian，Peng Gang，Long Xiao-hong.The solution of thermodynamic non-linear equation of SMA under complex stress state［J］.Journal of Huazhong University of Science and Technology:Natural Science Edition，2003，31(9):22-24.

［16］ Ma Hongwei，Cho Chongdu.Feasibility study on a super-elastic SMA damper with re-centering capability［J］.Materials Science and Engineering:A，2008，473:290-296.

［17］ 徐趙東，郭迎慶.MATLAB語言在建筑抗震工程中的應用［M］.北京:科學出版社，2004.

［18］ 彭凌云.向心式摩擦阻尼器的理論分析與應用研究［D］.北京:北京工業大學建筑工程學院，2004.