基于可靠性約束的熱固耦合結構拓撲優(yōu)化*

李冬梅 張憲民 王念峰 管貽生

(華南理工大學機械與汽車工程學院，廣東廣州510640)

式中，L為伴隨載荷矩陣，U2為伴隨載荷L產(chǎn)生的位移矩陣，u2為單元伴隨位移矩陣.

結構拓撲優(yōu)化的目的是尋求材料的最佳分布，以達到某種性能最優(yōu)化.柔順機構拓撲優(yōu)化設計的目的是在機構輸入端給定輸入后，高效地將其轉(zhuǎn)化為輸出端的輸出［1］.柔順機構的輸入可以是指定的力、位移、熱量和電信號等.若在輸入端加載熱源，則結構會產(chǎn)生熱應力，由此驅(qū)動柔順機構運動，這種機構稱為熱固耦合柔順機構.它的設計屬于多場耦合的設計范疇，拓撲優(yōu)化方法為其提供了工具［2］.由于不可避免地存在各種隨機因素，拓撲優(yōu)化研究正在由確定性拓撲優(yōu)化［3-4］向可靠性拓撲優(yōu)化方向發(fā)展［5-6］.

可靠性拓撲優(yōu)化的目的是以最少的材料和最低的造價來獲得性能更優(yōu)的結構［7-8］.目前柔順機構拓撲優(yōu)化的大量工作集中在力場或溫度場等確定性的物理場［9-10］中，所建立的模型絕大多數(shù)屬于確定性模型，即將結構幾何尺寸、材料特性、載荷環(huán)境、設計變量等均視為確定值.這在一定程度上簡化了結構的設計，降低了計算量.但實際中存在著各種誤差和不確定性因素，若未能合理考慮不確定性因素的影響，往往無法做出合理的分析與設計.Jung等［6］將可靠性分析與拓撲優(yōu)化方法相結合用于結構優(yōu)化中;Kharmanda等［7］提出了剛度最大化的可靠性拓撲優(yōu)化方法，在使用等量材料的情況下得到最大的結構剛度;Maute等［8］將可靠性拓撲優(yōu)化用于微機電系統(tǒng)(MEMS)的設計中.在國內(nèi)，羅陽軍等［11］以概率可靠性為約束，考慮多種參數(shù)的不確定性，得到了更合理的材料分布;占金青等［12］采用基礎結構法建立了可靠性拓撲優(yōu)化對偶數(shù)學模型，得到了性能比確定性拓撲結果更優(yōu)的柔順機構.迄今為止，雖然國內(nèi)外關于可靠性拓撲優(yōu)化的研究已有大量文獻，但主要集中在單一物理場中，有關多場耦合的可靠性拓撲優(yōu)化研究尚需補充和發(fā)展.

文中將可靠性方法和拓撲優(yōu)化方法相結合，在保證一定概率可靠性約束的條件下，尋找最優(yōu)的拓撲設計方案.考慮了材料屬性、幾何尺寸和溫度場的不確定性，采用一次二階矩法得到可靠性指標，然后以可靠性指標為約束條件，分別以結構柔度最小化和節(jié)點位移最大化為目標函數(shù)，建立熱固耦合結構的可靠性拓撲優(yōu)化數(shù)學模型，并使用數(shù)學規(guī)劃法進行求解.

1 耦合場隨機變量分析

物體受熱將產(chǎn)生熱膨脹，從而引發(fā)熱變形和位移.由機械載荷與溫度載荷共同作用的結構稱為熱固耦合結構，其有限元平衡方程為［13］

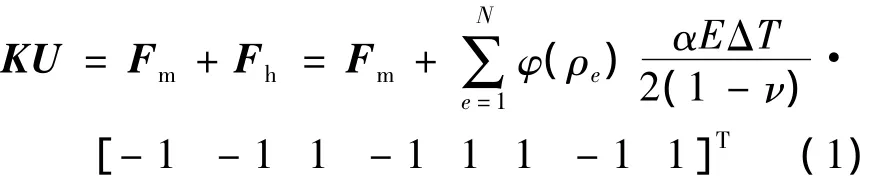
式中，K為結構整體剛度矩陣，U為位移列向量，F(xiàn)m為機械外載荷，F(xiàn)h為由溫度變化引起的熱載荷，φ(ρe)為與材料屬性相關的函數(shù)，ρe為單元相對密度設計變量，α為熱膨脹系數(shù)，E為彈性模量，ΔT為溫度變化，ν為泊松比，N為設計域節(jié)點總數(shù).

上述的分析是確定性分析，當材料屬性、溫度場及幾何尺寸隨機變化時，則式(1)應改寫為

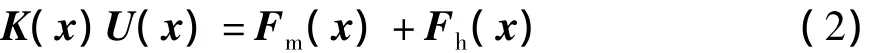
式中，x是由n個隨機參數(shù)組成的隨機向量，x= (x1，x2，…，xn)T.

設隨機變量均服從正態(tài)分布.以E為例，其均值為μE，標準差為σE，即E～N(μE，σ2E).隨機變量的標準差與均值的關系為

式中，γE為變異系數(shù)，當它為零時，表示該變量不具有隨機性，即為確定性參數(shù).

2 熱固耦合結構可靠性分析

以隨機向量x=(x1，x2，…，xn)T表示結構中的隨機因素，各隨機因素與結構功能狀態(tài)間的關系為

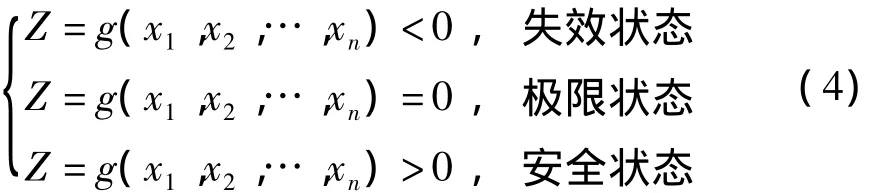
式中，Z=g(x1，x2，…，xn)=0為極限狀態(tài)方程，它將空間劃分為失效和安全兩個區(qū)域.結構處于失效狀態(tài)的概率為Pf，用一次二階矩法來求解Pf，通常是把基本隨機變量x=(x1，x2，…，xn)T映射為標準化空間的標準正態(tài)變量y=(y1，y2，…，yn)T，即

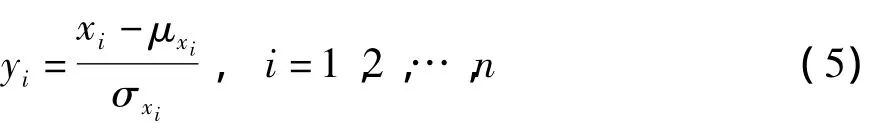
式中，yi～N(0，1)，μxi、σxi分別為隨機變量xi的均值與標準差.可靠度β的幾何意義為原點到失效面G(y)=0的最短距離［14］.Pf與β存在如下一一對應關系:

式中，Φ(·)為標準正態(tài)分布函數(shù).由式(6)可知，要使結構不失效，Pf要盡量小，可靠度β要盡量大.由此可將結構安全使用的條件轉(zhuǎn)化為具有足夠大的可靠性指標約束，即

式中，β*為許用可靠性指標，可以根據(jù)實際需要選擇.符合許用可靠性指標約束的正態(tài)隨機變量yi可由下式求出:

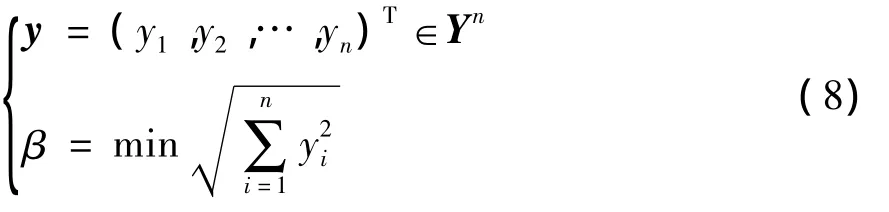
s.t.β(yi)≥β*.

可靠度對正態(tài)隨機變量的敏度為

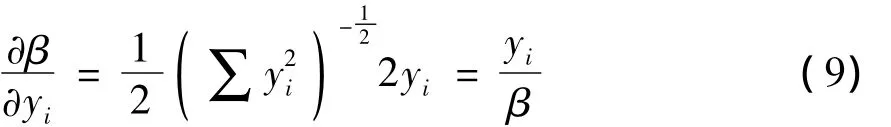
yi迭代的過程如圖1所示，B*為初始迭代點，根據(jù)迭代公式確定下一迭代點，直至滿足收斂條件.

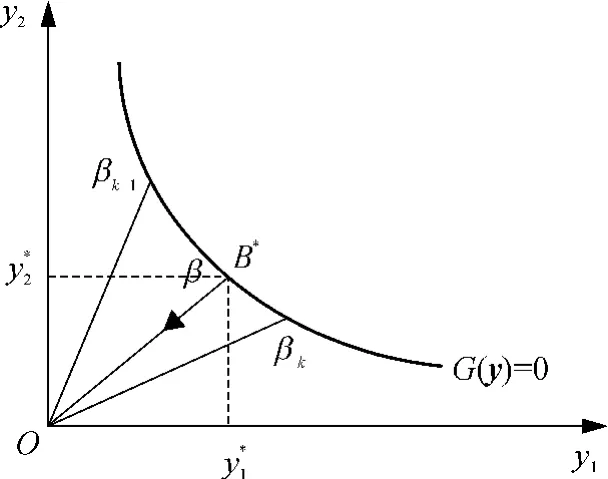
圖1 可靠性指標迭代搜索過程示意圖Fig.1 Schematic diagram of iterative search process of reliability index

3 可靠性拓撲優(yōu)化模型與敏度分析

3.1 熱固耦合結構的可靠性拓撲優(yōu)化數(shù)學模型

由方程(2)解出節(jié)點位移u后，可求出熱固耦合結構的剛度與柔度［13］.結構剛度可由應變能 C來表征.以結構應變能最小化為優(yōu)化目標，熱固耦合結構的可靠性拓撲優(yōu)化模型如下:

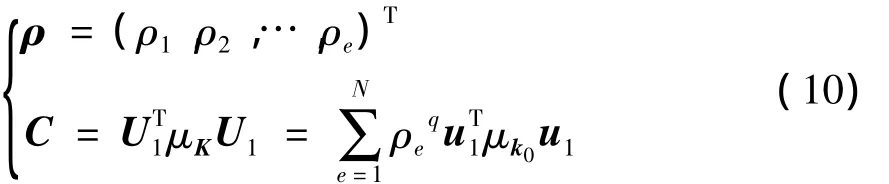
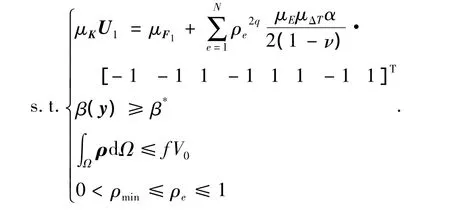
式中，U1為耦合場的整體位移矩陣，u1為單元位移矩陣，Ω為設計域，f為優(yōu)化體積比，V0為整個設計域的初始體積，F(xiàn)1為外力矢量，ρmin為單元相對密度的最小值，N為結構離散單元數(shù)，μE為彈性模量的均值(確定性部分)，μK、μk0分別為整體剛度矩陣的均值和優(yōu)化前單元剛度矩陣的均值，μΔT為溫度變化的均值，μF1為外載荷的均值，β*為給定的可靠性指標，q為懲罰因子.

機構的柔性可由互應變能(MSE)來表征［13］.以機構輸出位移最大化為優(yōu)化目標，熱固耦合柔順機構的可靠性拓撲優(yōu)化模型為

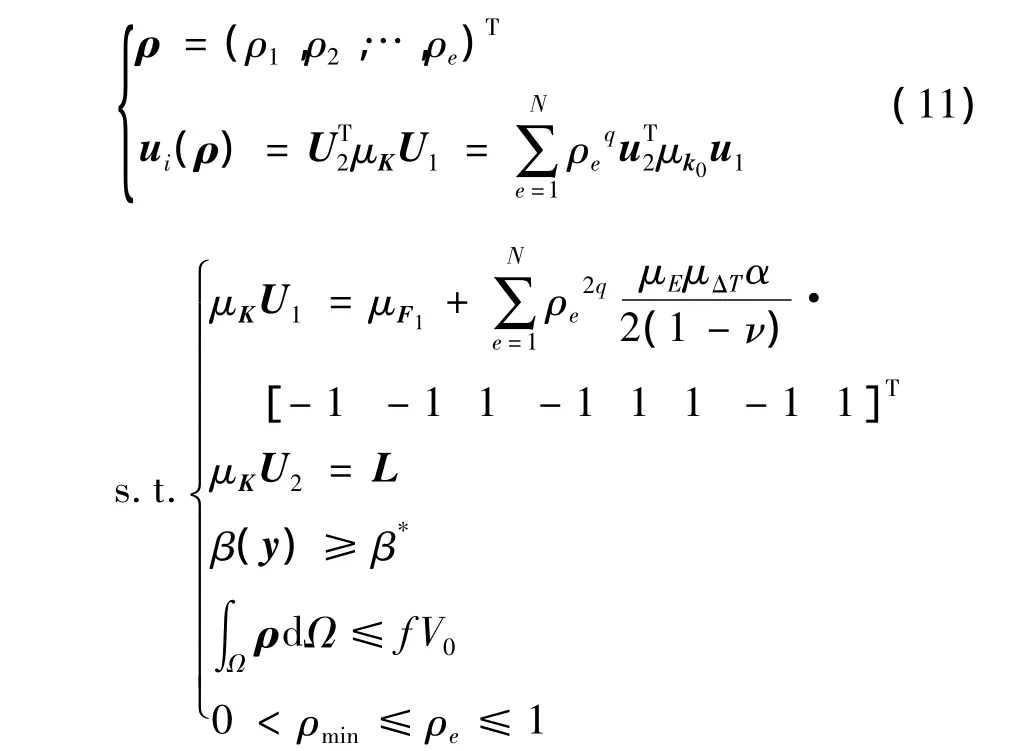
式中，L為伴隨載荷矩陣，U2為伴隨載荷L產(chǎn)生的位移矩陣，u2為單元伴隨位移矩陣.

3.2 敏度分析

文中采用伴隨矩陣敏度分析方法.自由度i處的位移ui可寫為ui=LTU.在L中除輸出位移自由度i處的載荷分量值設為單位力外，其他載荷分量均為0.位移敏度可寫為

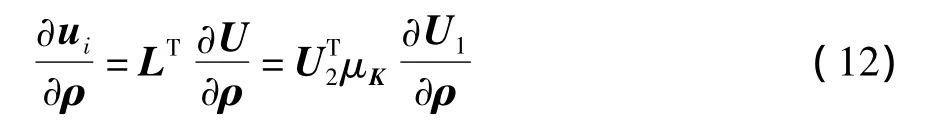
由于F1為給定的與設計變量無關的機械外載荷，則由平衡方程可推導出:

Fh為與設計變量相關的溫度載荷，由式(11)得

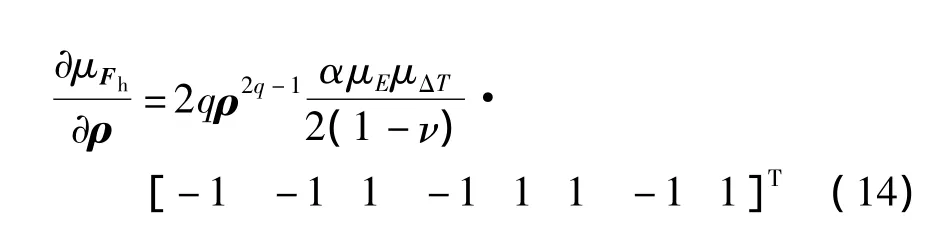
將式(13)、(14)代入式(12)得到結構位移的敏度:

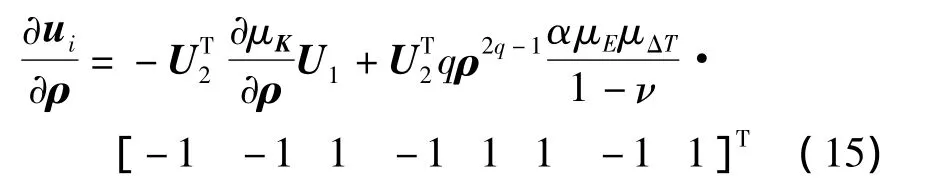
由式(10)可得

將式(14)代入式(16)得到結構柔度的敏度:

多場耦合的可靠性拓撲優(yōu)化流程如圖2所示.

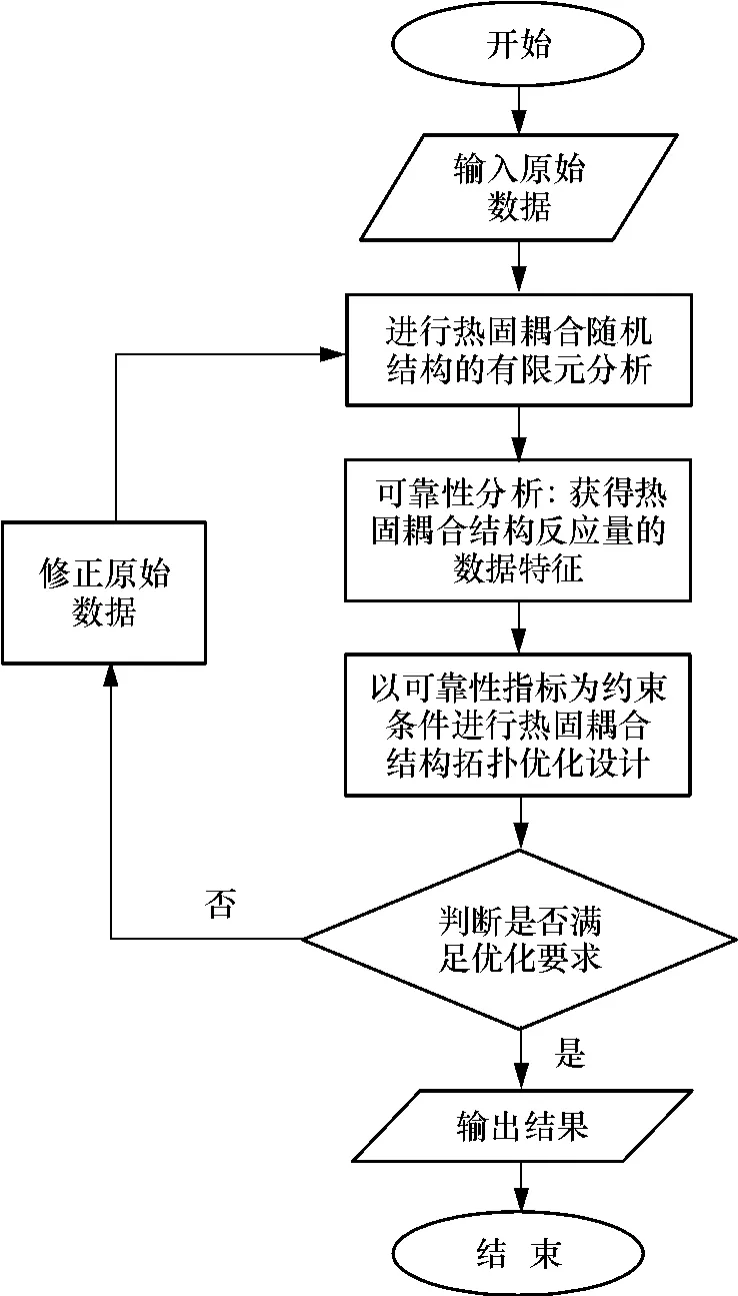
圖2 基于可靠性約束的熱固耦合結構的拓撲優(yōu)化流程圖Fig.2 Flow chart of topology optimization of thermo-mechanical coupling structures based on reliability constraint

4 數(shù)值算例分析

算例1 考慮如圖3所示的結構，對其均勻加熱，溫度變化ΔT=100K，在結構下邊中點處施加一機械外載荷F=10N.初始設計域為80mm×30mm，實體材料與整個設計域之比為0.5，熱膨脹系數(shù)α= 17.2×10-6/K，彈性模量與泊松比分別為 E=100 GPa、ν=0.3.在外載荷與溫度載荷共同作用下，獲得結構剛度最大化的可靠性最優(yōu)拓撲結構.

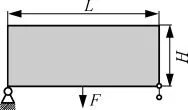
圖3 熱固耦合結構的設計域與邊界條件Fig.3 Design domain and boundary condition of thermo-mechanical coupling structure

以γL、γH、γF、γf、γΔT分別表示設計域的長和寬，外載荷、體積比和溫度隨機變量的變異系數(shù)(γi= σi/μi，i=L，H，F(xiàn)，f，ΔT)，采用正態(tài)分布3σ的準則描述隨機變量的變化范圍，得到反映隨機變量特征的參數(shù).可靠性拓撲優(yōu)化主要取決于隨機變量的均值和變異系數(shù)，表1中給出了通過求解式(10)表示的優(yōu)化模型得到的拓撲優(yōu)化結果.

表1中，模型a為確定性模型，各參數(shù)的變異系數(shù)為0;模型b和c為各隨機參數(shù)的變異系數(shù)為0.1的隨機模型，兩個模型中隨機參數(shù)具有相同的均值與標準差，但β*不同.對比模型b和c的拓撲優(yōu)化結果可知，隨著β*增大，應變能幾乎不變，優(yōu)化后結構的體積減小，說明優(yōu)化后結構性能不變，而材料的用量減少.因此模型c相對于b最大限度地滿足了經(jīng)濟性與安全性的要求.模型c和d的β*相同，除了溫度變異系數(shù)不同外其他參數(shù)的變異系數(shù)均相同.對比模型c和d可知，隨著ΔT的變異系數(shù)的增大，拓撲優(yōu)化結果更復雜.這是因為ΔT的變異系數(shù)的增加導致溫度載荷的不穩(wěn)定性增加，而溫度載荷是均勻分布在整個結構上的.

算例2 對圖4所示的位移轉(zhuǎn)向機構，在A點施加一水平機械外載荷Fin=10N，并且對其均勻加熱，溫度變化ΔT=100K.要求在機械載荷與溫度載荷共同作用下設計一種機構，其在B點垂直方向上的輸出位移最大.初始設計域為64 mm×64 mm，f= 0.35，附加在輸入端的彈簧剛度Kin=100N/m，輸出端彈簧剛度Kout=50 N/m.熱膨脹系數(shù)α=17.2× 10-6/K，彈性模量與泊松比分別為 E=100 GPa，ν=0.3.

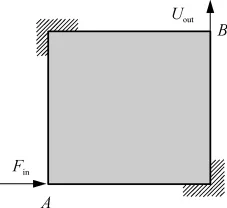
圖4 位移轉(zhuǎn)向機構設計域Fig.4 Design domain of displacement diverter

通過求解式(11)表示的優(yōu)化模型，可得其拓撲優(yōu)化結果，如表2所示.為了便于對比，本例中無論是確定性模型還是隨機模型都采用相同的體積比(f=0.35)，且γL=γH=γF=γΔT=0.1.

由表2中隨機模型的拓撲結果可知，隨著β*的增大，柔順機構的輸出位移也增大，表明機構的柔度增加.這說明在材料用量相同、各個隨機因素相同的情況下，可以通過可靠性拓撲優(yōu)化設計，獲得輸出位移更大、失效概率減小的柔順機構，即可通過控制失效概率和各參數(shù)的隨機性，改善柔順機構的功能(輸出位移)與性能(失效概率).從表2中還可知，可靠性熱固耦合拓撲機構的輸出位移比確定性熱固耦合拓撲機構的大，表明基于可靠性約束的熱固耦合拓撲設計得到的柔順機構具有更優(yōu)的性能，這說明進行可靠性拓撲優(yōu)化是非常必要的.

表1 不同可靠度及變異系數(shù)下的拓撲優(yōu)化結果Table 1 Topology optimization results corresponding to different reliabilities and variable coefficients

表2 不同可靠度下的位移轉(zhuǎn)向機構Table 2 Displacement diverter with different reliabilities

5 結語

文中將可靠性分析用于熱固耦合拓撲優(yōu)化中，用隨機溫度場及各物理參數(shù)的變異系數(shù)來表征各變量的隨機性和不穩(wěn)定性，提出一種基于概率約束的可靠性拓撲優(yōu)化設計方法，并進行了數(shù)值算例分析.結果表明，可靠性拓撲優(yōu)化可以找到經(jīng)濟性與安全性的最佳結合點，并能改善機構的功能，獲得性能更優(yōu)的柔順機構.這說明在拓撲優(yōu)化設計時進行可靠性分析是非常必要的.文中模型為多場耦合的可靠性拓撲優(yōu)化設計提供了一種有益方法.

［1］ 張憲民.柔順機構拓撲優(yōu)化設計［J］.機械工程學報，2003，39(11):47-51. Zhang Xian-min.Topology optimization ofcompliant mechanisms［J］.Chinese Journal of Mehanical Engineering，2003，39(11):47-51.

［2］ Li Qing，Grant P Steven，Xie Yi-min，et al.Evolutionary topology optimization for temperature reduction of heat conducting fields［J］.International Journal of Heat and Mass Transfer，2004，47(23):5071-5083.

［3］ Du Yi-xian，Chen Li-ping，Tian Qi-hua，et al.Topology synthesis of thermo-mechanical compliant mechanisms with geometrical nonlinearities using meshless method［J］.Chinese Journal of Solid Mechanics，2008，29(3): 256-262.

［4］ Hansen G，Bendsoe M P，Sigmund O.Topology optimization of heat conduction problems using the finite volume method［J］.Structural and Multidisciplinary Optimization，2006，31(4):251-259.

［5］ Kim Chwail，Wang Semyung，Bae Kyoung-ryun，et al.Reliability-based topology optimization with uncertainties［J］.Journal of Mechanical Science and Technology，2006，20(4):494-504.

［6］ Jung H，Seonho C.Reliability-based topology optimization of geometrically monlinear structures with loading and material uncertainties［J］.Finite Element in Analysis and Design，2004，41(3):311-331.

［7］ Kharmanda G，Olhoff N，Mohamed A，et al.Reliabilitybased topology optimization［J］.Structural and Multidisciplinary Optimization，2004，26(5):295-307.

［8］ Maute K，F(xiàn)rangopol D M.Reliability-based design of MEMS mechanisms by topology optimization［J］.Computurers and Structures，2003，81(8/9/10/11):813-824.

［9］ Bendsoe M P.Sigmund O.Topology optimization theory，methods and applications［M］.New York:Springer，2003.

［10］ Li Dong-mei，Zhang Xian-min，Guan Yi-sheng，et al.Topology optimization of compliant mechanisms with anisotropic composite materials［C］∥IEEE International Conference on Mechatronics and Automation.Xi'an: IEEE，2010:416-421.

［11］ 羅陽軍，亢戰(zhàn).連續(xù)體結構非概率可靠性拓撲優(yōu)化［J］.力學學報，2007，39(1):125-131. Luo Yang-jun，Kang Zhan.Non-probabilistic reliabilitybased topology optimization of continuum structures［J］.Chinese Journal of Theoretical and Applied Mechanics，2007，39(1):125-131.

［12］ 占金青，張憲民.基于基礎結構法的柔順機構可靠性拓撲優(yōu)化［J］.機械工程學報，2010，46(13):42-46. Zhan Jin-qing，Zhang Xian-min.Reliability-based topology optimization of compliant mechanisms by using foundation structure approach［J］.Chinese Journal of Mechanical Engineering，2010，46(13):42-46.

［13］ Li Dong-mei，Zhang Xian-min，Guan Yi-sheng，et al.Topology optimization ofthermo-mechanicalcontinuum structure［C］∥IEEE/ASME International Conference on Advanced Intelligent Mechatronics.Montreal:IEEE，2010:403-408.

［14］ Zhang Xian-min，Ouyang Gao-fei.A level set method for reliability-based topology optimization of compliant mechanisms［J］.Science in China Series E:Technological Sciences，2008，51(4):443-455.