訂貨問題的一個優化分析模型
錢杭靜
(浙江師范大學 數理與信息工程學院,浙江 金華 321004)
隨著科學技術的發展,社會生活的進步,商業公司訂貨時有著越來越多的選擇,如何制定訂貨策略成了商業公司生產銷售環節中很重要的一環,因此對商業公司訂貨問題的研究對商業公司的運營具有重要的意義。
1 訂貨問題敘述
某商業公司管理著5個倉庫 (B1~B5)和8個分店(C1~C8),主要經營 10種物資,而這些物資全部向 3個工廠(A1~A3)進貨。公司的工作流程是根據8個分店的銷售需要,先向工廠訂貨,然后將各種物資運送到倉庫,再由倉庫運送到分店進行銷售(分店只消耗物資,不儲存物資)[1]。
各個工廠生產10種物資的全部或部分物資的年產量和各種物資單價、每個工廠到每個倉庫的運輸單價及每個倉庫的容量參見參考文獻[1]。同種物資在不同的倉庫的庫存費一樣,而不同物資的庫存費是不同的。每種物資有著自己的體積,物資的庫存費與單位占用庫容、5個倉庫到8個分店的運輸單價及8個分店對物資的年需求量參見參考文獻[1]。
公司每次訂貨都會有其他的各種花費,稱為訂貨費,設公司每次的訂貨費為1萬元。另外,一次訂貨可使用的流動資金上限為100萬元,如果進行銷售時允許缺貨,但缺貨的損失費是存儲費的2倍。建立模型解決公司一年之中應該怎樣組織訂貨,并使得總花費最少。
2 問題分析
要確定組織訂貨的方式,首先從一次訂貨進行考察,一次訂貨總費用分為五部分,分別為運輸費、購物費、定貨費、庫存費、缺損費[2]。對上述五部分分別進行分析建立模型,并結合題意,列出多個等量關系、不等關系作為約束條件,進而求得總費用的模型,編程求得最佳方案使得總費用最少。
3 優化模型建立
在建立模型時,為使模型簡單、易于理解、便于計算,作如下假設:
(1)假設每次訂貨情況完全一致,且每種貨物出售狀況均為穩定售出[3];
(2)假設倉庫在每一次訂貨后各種貨物均勻減少,且同時售完,但下一次貨物會立即補充,剛好售完與立即補充之間的時間間隔很短,可忽略不計;
(3)假設每件產品庫存不到一年均按照一年的庫存費用算,缺損費每次訂貨均攤。
對符號定義如下:
D=(D1,D2,…,D10):10 種物資一次訂貨總量矩陣;
S1:一次訂貨3個工廠生產10種物資產量矩陣;
S2:一次訂貨3個工廠到5個倉庫的運輸量矩陣;
S3:一次訂貨5個倉庫到8個分店的運輸量矩陣;
S4:一次訂貨10種物資到5個倉庫的分配矩陣;
T0:一次訂貨總耗費;
T1:一次訂貨購買費;
T2:一次訂貨A→B運費;
T3:一次訂貨B→C運費;
Mstr:10種物資的單件庫存費矩陣;
R1:3個工廠生產10種物資單價矩陣;
R2:3個工廠到5個倉庫的運輸單價矩陣;
R3:5個倉庫到8個分店的運輸單價矩陣;
P:分店總體對10種物資的年總需求量矩陣;
[*]′:* 的轉置 矩陣 ;
[*]i:*的第 i個行向量;
[*]i′:* 的第 i個 列向 量。
優化分析模型,確定商業公司的訂貨方式使總費用最少。
由于一次訂貨過程中各種物資流通總量不變,只是分配方式不同,則可以建立如下等量關系。
由于一次訂貨各物資總量守恒,即:

根據一次訂貨過程中3個工廠生產總量與輸出總量相同,即:

由于一次訂貨過程中各倉庫物資輸入總量與各倉庫運往分店的輸出總量相同,即:

再由一次訂貨過程中,運往各倉庫的各種物資總量與一次訂貨過程中各種物資的生產總量相同,即:

又根據一次訂貨過程中各倉庫物資的庫存總量與一次訂購過程中各倉庫物資的輸入總量相同,即:

一次訂貨過程中購買費為:

一次訂貨過程中,物資從3個工廠運往5個倉庫的總運費為:

一次訂貨過程中,物資從5個倉庫運往8個分店的總運費為:

一次訂貨過程中,總費用等于五部分費用總和,即:

一次訂貨過程中,總費用不超過給定的一次訂貨過程中的流動資金:

N次訂貨過程中,各種物資訂購總量不超過整個過程中,8個分店對各種物資的總需求量,即:

N次訂貨過程中運往各個分店的物資總量不超過各個分店對物資總量的需求量,即:

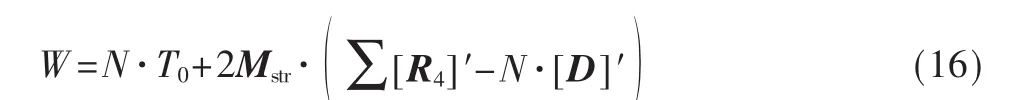
4 求解
N次訂貨過程中從3個工廠中訂購的各種物資總量不超過3個工廠中各種物資的年產量,即:

假設存在N+1次訂貨過程,則N+1次訂貨過程中各種物資的訂購總量超過分店對各種物資的年總需求量,即:

N次訂貨過程中各種物資的訂購總量不超過分店對各種物資的年總需求量,即:

整個訂貨過程中總費用為N次訂貨過程中總費用與缺損費之和,即:
將式(1)~式(16)用 LINGO編程處理,得到部分核心數據,計算得到的最佳解決方案為:


由上述結果可知,按照分析得到的一次訂貨方式進行訂貨,則最后一次訂貨過程中物資總量可以處于不飽和狀態,但訂貨方式仍與之前的訂貨方式一致。由此可知,總訂貨次數為15次,缺損費實際均攤到每一次訂貨過程中,并且每次訂貨過程中100萬流動資金可以得到充分利用。
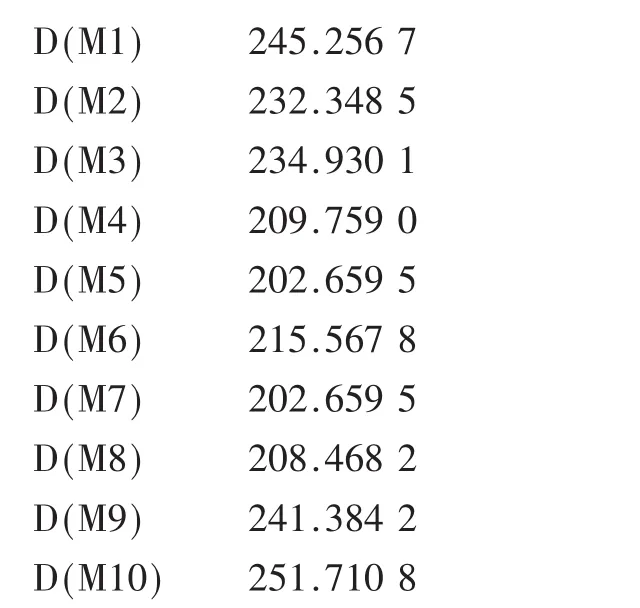
每次訂貨過程中各種物資訂購總量為:
每次訂貨過程中3個工廠運往5個倉庫和5個倉庫運往8個分店的運輸方案分別如表1、表2所示。實際問題中每一次的訂貨狀況不一定相同,且并非周期性訂貨,即存在出售高峰期和出售低谷期。但在本文假設條件下,即每次訂貨狀況相同,將復雜問題簡單化,分析得到的訂貨方式能夠在很大程度上解決問題。
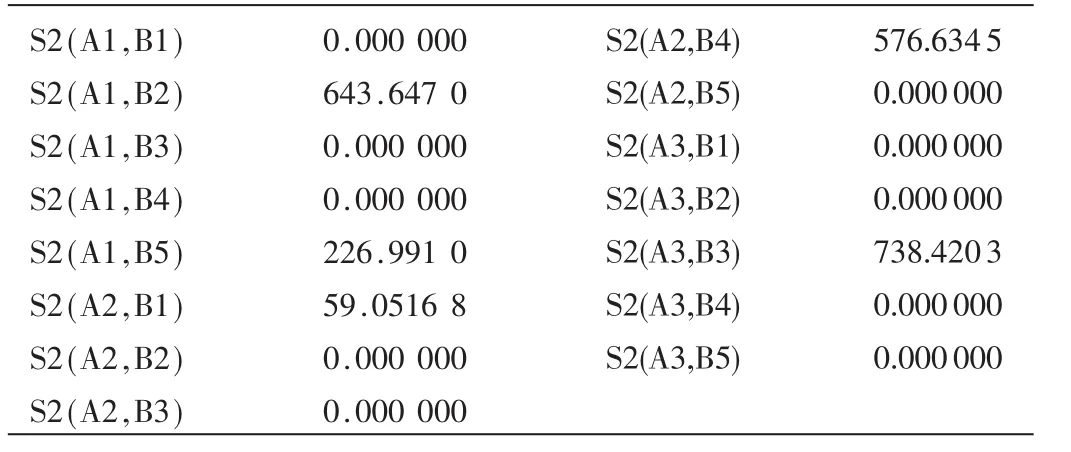
表1 3個工廠運往5個倉庫的運輸方案
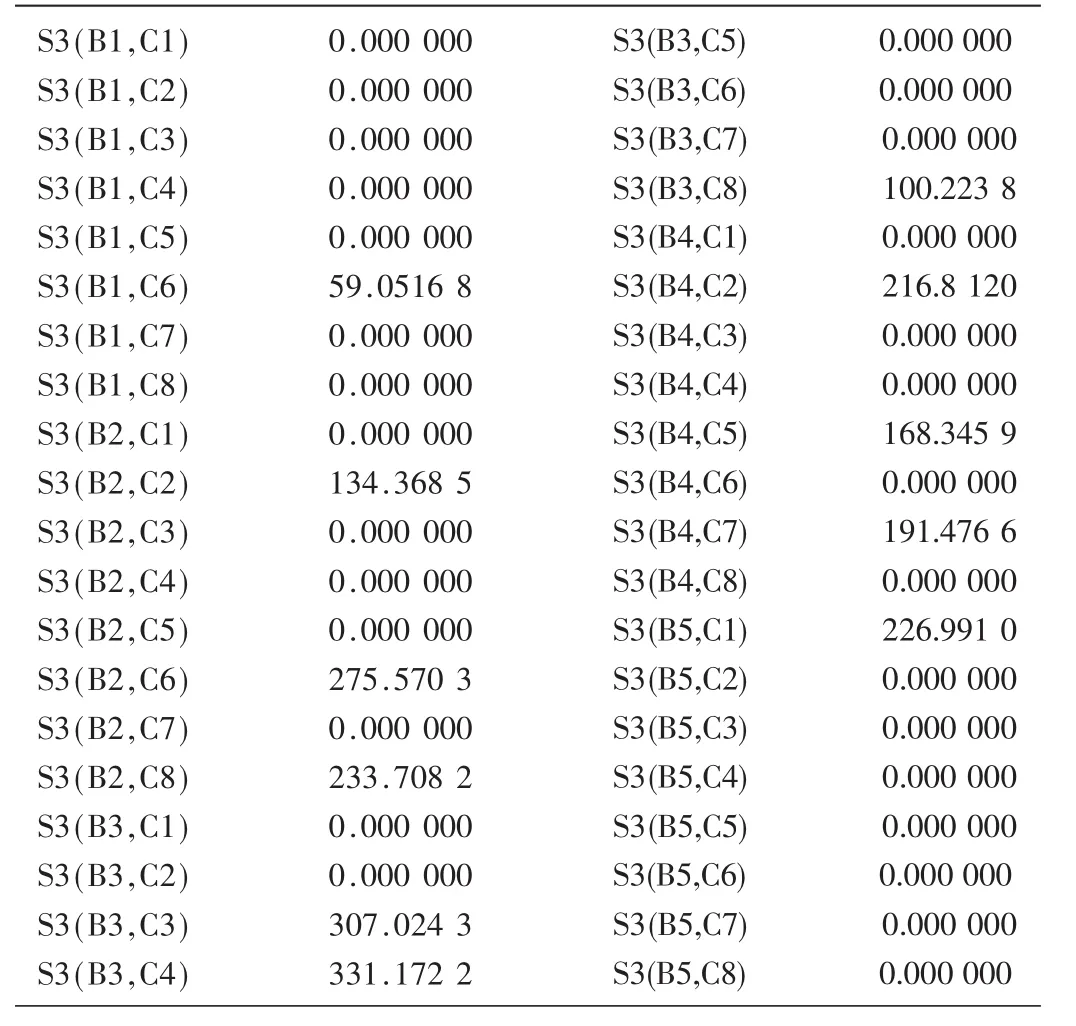
表2 5個倉庫運往8個分店的運輸方案
[1]公司訂貨問題.MATLAB中文論壇:http://www.ilovematlab.cn/thread-83116-1-1.html.
[2]杜廷松.訂貨問題的一個最優存儲模型[J].商場現代化,2007(500):11.
[3]史玉敏.基于價格有折扣的零售商訂貨問題[J].物流技術,2008,27(8):102-104.

