庫水位驟降時壩坡穩定性分析研究

劉英泉,王成言

(中水北方勘測設計研究有限責任公司,天津300222)

土石壩壩坡穩定性決定于它的幾何形狀、土體材料屬性及其內外部受力情況。在目前的研究中,認為孔隙水壓力和庫水壓力是影響壩坡穩定性的主要荷載[1-2]。庫水位的變化會引起土體中孔隙水壓力的瞬態變化,同時庫水壓力的變化也會產生壩坡內部超孔隙水壓力的發展[3-4]。當庫水位下降過快,沒有給排水提供足夠的時間,對于滲透系數較小的土體,其孔隙水壓力不會在水位驟降期以同樣的速率伴隨著水位的下降而消散。因此,研究低滲流土體在庫水位驟降期的特性是很有必要的[5-7]。

本文研究庫水位驟降時,壩坡滲流場及穩定性的變化情況,并用有限元法研究不同工況下孔隙水壓力隨水位驟降的變化;將計算得出的不同時刻孔隙水壓力值應用于采用極限平衡法,分析邊坡穩定性。在理論研究的基礎上,結合某均質土石壩具體情況對其滲流場變化條件下的壩坡穩定性進行分析,總結了壩坡穩定性對庫水位變化的響應情況。

1 基本理論

在實際工程中,降雨入滲和庫水位變化中的土壩滲流都應該考慮非飽和區的作用。考慮非飽和滲流的邊坡穩定分析問題以及求解比較復雜,包含了巖土體、水、空氣以及收縮膜四相的互相耦合問題。本文分析庫水位驟降時壩體的浸潤線變化和孔隙水壓力的變化。

根據達西定律,多孔飽和不可壓縮連續介質滲流可表示為:

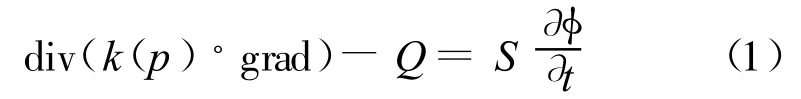
式中:φ為總流體勢或總水頭;k(p)為介質的滲透系數;Q為源、匯項;S為儲水系數。

其中

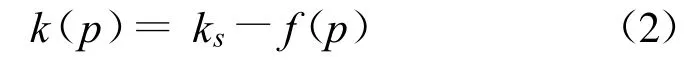
式中:ks是飽和滲透系數,為常數;f(p)為關于壓力水頭p的光滑連續函數[1]。

結合有限元理論,由式(1)可得:

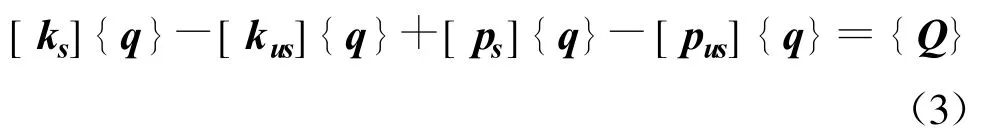
式中:[ks]為飽和單元滲透系數矩陣;[kus]為非飽和單元滲透系數矩陣;[ps]為飽和單元孔隙率矩陣;[pus]為非飽和單元空隙率矩陣;{q}為節點水頭向量;{Q}為臨界節點流向量。

微分方程(3)整合了時間域,結合平衡方程和連續方程,可以通過迭代計算出自由面及滲流場分布。

通過有限元瞬態滲流分析得出水位驟降后某一時刻自由面,對于滑動面在浸潤面以下的情況,可采用考慮孔隙水壓力影響的有效應力方法來計算土坡的安全系數,再結合Morgenstern-Price提出的非飽和土體的強度理論,土質邊坡的安全系數公式可寫為:

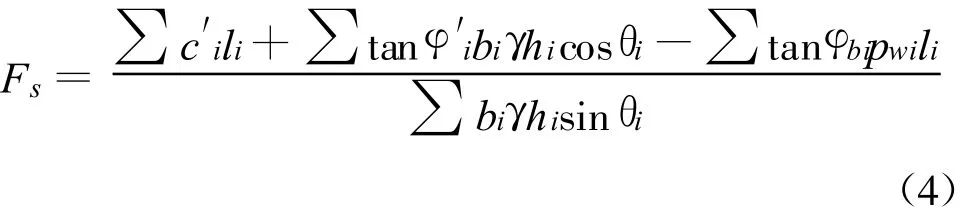
式中:Fs為邊坡穩定系數;c′i,φ′i為土體的有效應力抗剪強度指標;φbi表示由于基質吸力增加引起抗剪強度增加的吸力摩擦角;γ為土的天然容重;θi為條塊底面中點的切線與水平面的夾角;bi為土條寬度;pwi為孔隙水壓力;hi為土條高度;li為土條滑動面最大弦長。

根據式(4)結合有限元滲流分析得出的孔隙水壓力等結果,定義材料參數后可搜索出臨界滑移面,計算出壩坡安全系數。

2 實例分析

2.1 非穩定滲流場分析

2.1.1 計算模型

某水利樞紐工程位于陜北黃土高塬南部的黃土梁峁區,攔河壩為均質土壩,大壩壩頂高程852.0 m,壩頂寬度10 m,最大壩高66.0 m,壩頂總長度為502.0 m;上游壩坡坡比為1∶2.75和1∶3,在830 m高程處設置3 m寬的馬道;下游壩坡坡比均為1∶2.75,在836 m高程和816 m高程處設置2 m寬的馬道。上游壩坡采用0.4 m厚的干砌石護坡,下游壩坡采用漿砌石網格內植草護坡,并在壩體內設置水平褥墊排水,排水褥墊深入壩體內140 m,布置形式見圖1。

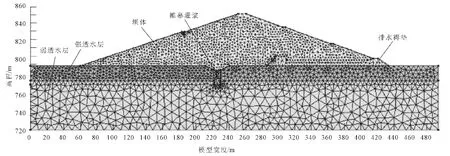
圖1 計算模型網格剖分圖

根據項目具體情況取河床壩段最大壩高處建立如圖1所示有限元模型。邊界條件為:上游邊界條件隨時間變化,即從高程848 m到高程800 m進行瞬態分析。壩基的上游側面、下游側面以及底面為零流量邊界;強透水層上游頂面及下游頂面、上游庫水位以下的壩坡表面及下游尾水位以下的下游壩坡表面為定水頭邊界。

運用Geo-Studio建立起二維有限元模型,包括壩體、防滲帷幕、排水褥墊、強透水層、弱透水層五個區。該有限元計算模型共剖分了 2 582個節點,4 536個單元。模型滲流、穩定計算參數和計算工況分別如表1、表2所示。

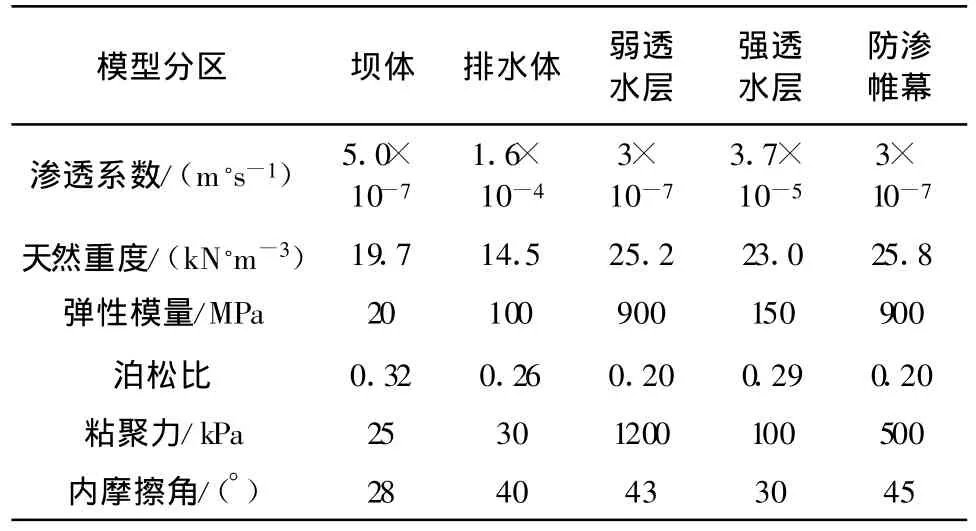
表1 滲流、穩定計算所需參數表

表2 計算工況

2.1.2 計算結果分析

圖2～圖5為庫水位以不同速度下降時壩體浸潤線位置的變化圖。圖中的數字是浸潤線位置的時刻(單位:d)。

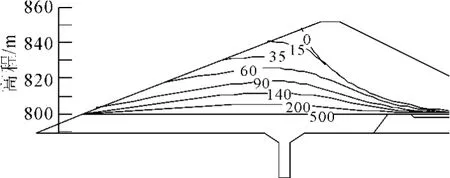
圖2 工況1時浸潤線位置變化圖

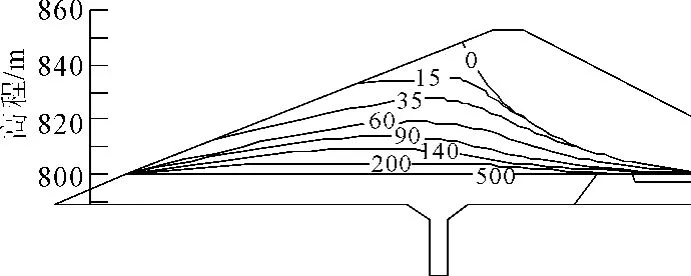
圖3 工況2時浸潤線位置變化圖

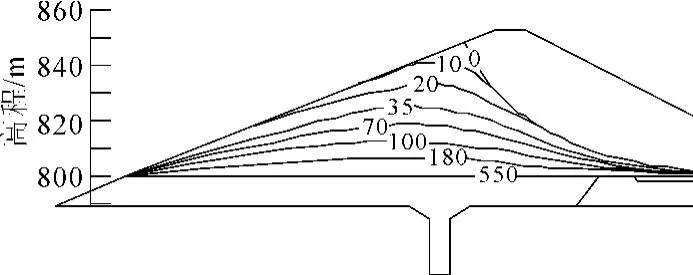
圖4 工況3時浸潤線位置變化圖

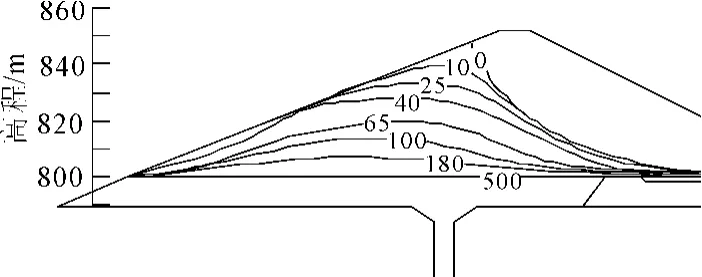
圖5 工況4時浸潤線位置變化圖

庫水位下降速度為0.5m/d時(如圖2),浸潤線在35 d后才出現上凸形狀,且不是特別嚴重;當庫水位降至800 m時,浸潤線最高點高程為808 m。在庫水位下降速度為1 m/d時(如圖3),浸潤線變化滯后于壩前水位變化而出現向上游壩坡滲流的現象仍較明顯,浸潤線形狀上凸;當庫水位降至800 m時,浸潤線最高點高程為818 m。

當庫水位下降速度為1.5m/d時(如圖4),浸潤線滯后現象更為明顯。庫水位下降速度為2 m/d時(如圖5),“逆流”現象最嚴重,在10 d時,壩前水位已經降到828 m,而浸潤線最高點高程為843 m,且出現在上游壩面。靠近上游壩面的壩體大多還是飽和的,壩體內浸潤線回落嚴重滯后于庫水位下降的速度。

由圖2～圖5可以看出,隨著庫水位下降,壩體內的浸潤線也隨之下降,壩體內浸潤線下降有明顯的滯后現象。部分水由于孔隙水壓力來不及消散而滯留在壩體內,使得浸潤線呈現“上凸”的曲線形狀。壩體內自由水面高于上游庫水位,形成“逆流”現象。水位下降速度越快,“逆流”現象越明顯。不同水位下降速度下,浸潤線在經過450 d后都基本上趨于穩定。

2.2 上游壩坡穩定性分析

庫水位驟降情況下壩體內孔隙水壓力消散滯后及上游壩坡的“逆流”現象定會對上游壩坡穩定性造成不利影響。圖6為不同工況下上游壩坡安全系數隨水位下降時間變化情況圖。

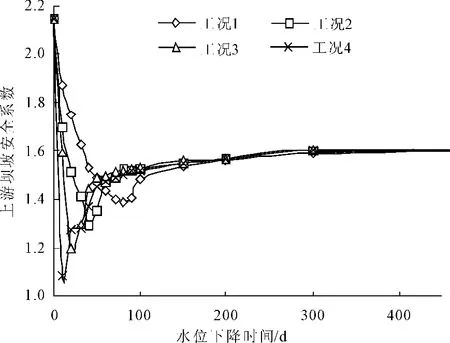
圖6 庫水位下降時上游壩坡的安全系數變化曲線圖

上游壩坡的安全系數隨庫水位變化,原因如下:第一,壩前水體對壩體的靜水壓力有利于上游壩坡穩定,上游水位下降自然導致上游壩坡穩定安全系數降低;第二,庫水位下降過快,壩體內孔隙水壓力來不及消散而形成向上游壩坡的反向滲流所致。滲透力在庫水位下降過程中是變化的,滲透力達到最大值的時候壩坡安全系數將達到最小值。

由圖6可看出,工況4為水位下降速度最快的工況,其上游壩坡安全系數谷值最小且達到谷值所需時間最短。結合工況4～工況1,水位下降速度越慢,上游壩坡安全系數所達到的低谷值越小,達到低谷值的時間也越長。水位下降速度越快滲透力越容易達到最大值,隨著水位驟降速度的減慢,壩坡穩定系數的最小值逐漸變大,發生的時間也越晚。因此,水位驟降速度是影響上游壩坡穩定性的重要因素,水位驟降速度越大對上游壩坡穩定性不利。

3 結 論

本文考慮非飽和條件下某工程非穩定滲流,將滲流場模擬得出的孔隙水壓力等結果應用于上游壩坡的穩定性分析中,得出以下結論:

(1)在庫水位驟降情況下,壩體內的浸潤線隨之下降,但有明顯的滯后現象。部分水由于孔隙水壓力來不及消散而滯留在壩體內,壩體內浸潤線高于上游庫水位,形成向上游壩坡的“逆流”。“逆流”現象產生的滲透壓力對上游壩坡穩定性產生不利影響。

(2)庫水下降速度不同時,開始出現“逆流”現象以及形成穩定滲流場的時間是不一樣的。庫水位下降速度越快,上游壩坡穩定性降低速度及幅度越大。

[1] 沈珠江.廣義吸力和非飽和土的統一變形理論[J].巖土工程學報,1996,18(2):1-9.

[2] 劉新喜,夏元友,張顯書,等.庫水位下降對滑坡穩定性的影響[J].巖石力學與工程學報,2005,24(8):1439-1444.

[3] 鄧祥輝.等效連續巖體的滲流應力耦合模型研究及應用[J].西安工業大學學報,2009,29(6):585-588.

[4] 劉新喜,夏元友,練操,等.庫水位驟降時的滑坡穩定性評價方法研究[J].巖土力學,2005,26(9):1427-1431.

[5] 王學武,許尚杰,黨發寧,等.水位驟降時的非飽和壩坡穩定分析[J].巖土力學,2010,31(9):2760-2764.

[6] 賈蒼琴,黃茂松,王貴和,等.水位驟降對土坡穩定性的影響分析[J].同濟大學學報(自然科學版),2008,36(3):304-309.

[7] Lane P A,Griffiths D V.Assessment of stability of slopes under drawdown conditions[J].Journal of Geotechnique Geoenvironment Engineering,2000,126(5):443-450.