基于改進(jìn)HHT 的水中爆炸沖擊波信號時頻特性分析方法*

程 擂，韓 焱，王 鑒，杜 娟

(中北大學(xué)電子測試技術(shù)國家重點(diǎn)實(shí)驗室，山西 太原030051)

水中爆炸沖擊波信號是一種瞬態(tài)非平穩(wěn)信號，特點(diǎn)是持續(xù)時間短、頻帶寬。常用的分析方法有3種:時域分析、頻域分析和時頻域分析。希爾伯特-黃變換(HHT)［1］是1998 年美國黃鍔提出的一種處理非平穩(wěn)信號、且在實(shí)踐中得到充分驗證的時頻域信號處理手段，一些研究者將其應(yīng)用到了沖擊信號等非平穩(wěn)信號的分析中，并且取得了一定的成果。賴思邈等［2］利用HHT 對水下目標(biāo)特征進(jìn)行提取，結(jié)果表明HHT 適用于水聲非平穩(wěn)信號的分析，并且有很強(qiáng)的自適應(yīng)特性和較好的時頻聚集性。宋敬利等［3］利用HHT 方法分析了某型艦船在非接觸水下爆炸作用下典型部位沖擊響應(yīng)信號，計算了Hilbert 幅值譜、Hilbert 能量譜和Hilbert 瞬時能量，探討了非接觸水下爆炸作用下艦船沖擊響應(yīng)的時頻特征。

HHT 處理非平穩(wěn)信號效果很好，但仍存在一些問題:第1，在低頻處會產(chǎn)生一些幅度很小的錯誤固有模態(tài)函數(shù)(IMF);第2，在高頻處的第1 級固有模態(tài)函數(shù)，其頻帶寬度過大，并不是單一組分;第3，由于干擾問題的存在，相鄰的IMF 分量不能被很好地區(qū)分。另外，HHT 還很容易受到噪聲的干擾［4］。

本文中，提出一種改進(jìn)的HHT 算法，用來對水中爆炸沖擊波信號進(jìn)行時頻分析:首先，采用小波分層的方法對信號進(jìn)行預(yù)處理，將輸入信號分為多個窄帶子信號的結(jié)合，使得每一個IMF 為單一組分;第2，采用基于相關(guān)系數(shù)的IMF 選取原則，對所有的IMF 分量進(jìn)行篩選，消除錯誤的IMF 分量。

1 改進(jìn)的HHT

1.1 HHT

HHT 是一種新的時頻分析方法，基本思路是:以瞬時頻率為出發(fā)點(diǎn)，為了分析信號的瞬時頻率，希望把信號分成由有物理意義的瞬時頻率的各個信號分量的組合，包括經(jīng)驗?zāi)B(tài)分解(EMD)和希爾伯特變換［1］2 個部分。

1.1.1 經(jīng)驗?zāi)B(tài)分解

經(jīng)驗?zāi)B(tài)分解包括原始信號在連續(xù)模式下的信號分解。從原始信號中得到的模式對于信號s 的分解可以寫為式中:ci為第i 分量，稱作固有模態(tài)函數(shù)(IMF)，TM是余數(shù)。

IMF 需要滿足2 個條件:(1)整個數(shù)據(jù)區(qū)間內(nèi)，極大值和極小值的個數(shù)需要相同或者最多相差±1;(2)由每個極小值和極大值產(chǎn)生的包絡(luò)平均必須為零，而且要求分解到最后時，剩下的余數(shù)不能有極值。

首先，找到信號s［n］的極值點(diǎn)，用包絡(luò)線分別將上下極值點(diǎn)連接起來，得到上包絡(luò)線u1和下包絡(luò)線l1，然后算出上下包絡(luò)線的均值，記作m1。此時m1與原始信號之差

驗證是否滿足IMF 需滿足的2 個條件。若是，則令c1=h1;若不是，則將h1作為原始數(shù)據(jù)重復(fù)上述過程

直到找出符合條件的hk，令其為c1，即求出了IMF 的第1 個分量c1。其次計算

r1(n)仍然包含原始數(shù)據(jù)的頻率信息，因此將r1(n)作為新信號，重復(fù)步驟(1)～(4)，循環(huán)k 次，直到解出的IMF 分量ck或者殘余信號rk非常小或為單調(diào)時，循環(huán)結(jié)束。

1.1.2 希爾伯特變換

通過希爾伯特變換，求出幅度-時間-頻率的三維表示。定義一解析信號

式中:SH［n］為s［n］的希爾伯特變換

在極坐標(biāo)下用指數(shù)表示為

根據(jù)式(9)即可做出幅度-時間-頻率的三維表示圖。

1.1.3 希爾伯特邊緣譜

定義了希爾伯特譜后，如在時間上對其進(jìn)行積分，即可求得其希爾伯特邊緣譜

與傅立葉頻譜相似，希爾伯特邊緣譜表示了一個在各個頻率處幅值或能量的分布圖。

1.2 改進(jìn)的HHT

針對HHT 的缺陷，首先通過小波分析將原始信號分成不同頻段子信號的預(yù)處理方法。小波的多分辨分析特性能將信號在不同尺度下進(jìn)行多分辨率的分解，并將交織在一起的各種不同頻率組成的混合信號分解成不同頻段的子信號。對于一個N 層分解來說，共有N+1 個途徑分解信號。在爆炸沖擊波信號中，高頻部分為主要分析部分，因此采用如圖1 所示的小波分解。其中A 代表高頻分量，D 代表低頻分量。

通過N 層小波包分解，原始信號被分解成為N+1 個不同頻段的子信號，且每一個子信號具有很窄的頻帶，避免了EMD 分解產(chǎn)生非單一組分IMF 的情況。然而該預(yù)處理會使IMF 分量增加，其中會包含許多錯誤的IMF 分量。

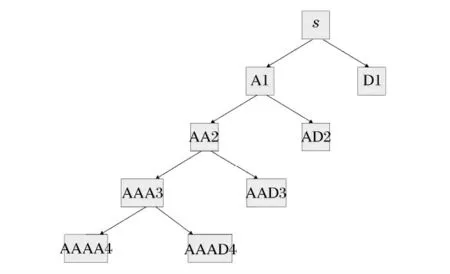
圖1 基于爆炸沖擊特征的小波分解Fig.1 Wavelet decomposition based on the characteristic of explosion shock wave

理想中正確的IMF 分量將會包含原始信號中所具有的頻率成分，因此這些IMF 分量與原始信號應(yīng)具有良好的相關(guān)性。根據(jù)這一特性，采用基于IMF 分量與原始信號相關(guān)系數(shù)的選取原則，來對產(chǎn)生的IMF 分量進(jìn)行篩選，將低頻處幅度很小的錯誤IMF 以及通過小波包分解產(chǎn)生的錯誤IMF 去除。設(shè)產(chǎn)生的第i 級IMF 分量ci與原始信號的相關(guān)系數(shù)為ri，根據(jù)相關(guān)系數(shù)的定義，則

設(shè)定一閾值ρ，根據(jù)ρ 對每一個IMF 分量與原始信號的ri進(jìn)行對比。若ri＞ρ，則將該IMF 分量保留，若ri＜ρ，則認(rèn)為該IMF 分量為錯誤分量，將其去除。ρ 可以通過以下方式確定

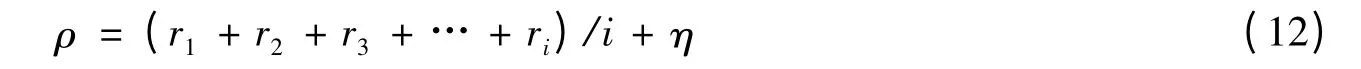
式中:η 的選擇取決于所需IMF 分量的程度，ρ 越大，IMF 分量越少，反映的高頻信號越明顯，但因此可能會丟失某些頻率的信息;ρ 越小，所包含高頻信號的信息越豐富，但高頻信號的反映相對較差。

2 數(shù)值模擬與實(shí)驗

2.1 數(shù)值模擬

在上述討論的基礎(chǔ)上，對模擬出的爆炸沖擊波信號進(jìn)行數(shù)值分析。爆炸沖擊波的數(shù)學(xué)表達(dá)式為

式中:Ps為常數(shù)，1≤Ps≤3，b=0.5+Ps;t0可以利用Josef Henrych 的經(jīng)驗公式來計算，即t0=(0.107+0.444R+0.264R2－0.129R3+0.033 5R4)W1/3，其中0.05 ≤R ≤3，W 為炸藥質(zhì)量，kg。

模擬出的爆炸信號如圖2(a)所示。圖2(c)為加入海洋噪聲后的模擬水中爆炸沖擊波信號，噪聲如圖2(b)所示。

對該信號進(jìn)行HHT，得出該模擬爆炸沖擊波信號經(jīng)EMD 分解后的IMF 分量，信號的HHT 時頻表示圖如圖3 所示。從圖3 中可以看出，分量c1包含了高頻及低頻信息，其頻帶過寬，不能成為單一組分;分量c6、c7及c8為幅度很小的錯誤IMF 低頻分量。在希爾伯特能量譜的時頻表示圖中，爆炸沖擊波信號的高頻部分不能很好地被表現(xiàn)出來，通過局部放大后方可觀察到具有高能量的高頻信息(如圖3(b)放大圖中的白點(diǎn)部分)。

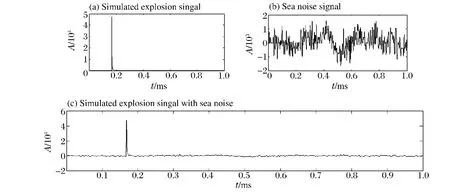
圖2 模擬爆炸沖擊波信號Fig.2 Simulated explosion shock wave

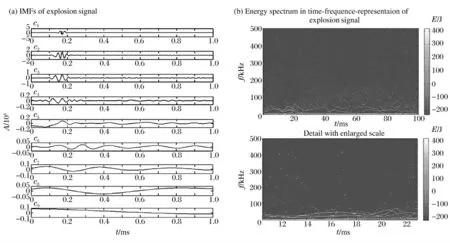
圖3 模擬水中爆炸沖擊波信號的IMF 及HHT 能量分布時頻圖Fig.3 IMF and HHT time-frequency representation of simulated underwater explosion shock wave

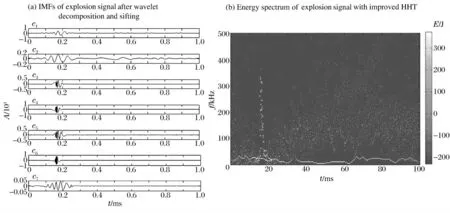
圖4 改進(jìn)后的模擬水中爆炸沖擊波信號IMF 及HHT 能量分布時頻圖Fig.4 IMF and HHT time-frequency representation of simulated underwater explosion shock wave using improved HHT

利用HHT 改進(jìn)算法對信號進(jìn)行處理，得出經(jīng)篩選后的IMF 分量(如圖4(a)所示)，對其進(jìn)行希爾伯特變換，得出改進(jìn)的HHT 時頻表示圖，如圖4(b)所示。

通過圖4 可以看出，經(jīng)過小波分層以及相關(guān)系數(shù)篩選后，爆炸沖擊波信號的IMF 分量中去除了幅度較小的錯誤低頻分量，在高頻部分中頻率信號也較為單一，更好地反映了爆炸沖擊波信號的EMD 分解。而在能量分布時頻表示圖中，沖擊信號中的高頻部分被有效地體現(xiàn)出來(如圖4(b)中在10 ～20 ms 處的白點(diǎn))，通過該圖可以看出改進(jìn)的HHT 算法有效地去除了錯誤的低頻干擾。對比圖3 與圖4 的IMF 分量以及HHT 能量時頻表示圖可以看出，改進(jìn)的HHT 解決了在原始HHT 變換中存在的問題，能夠更好地反映出信號的時頻特征圖。

2.2 水中爆炸實(shí)驗

圖5 所示為水面下70 cm 處，10 g TNT 炸藥的實(shí)測爆炸沖擊波信號，沖擊波傳感器位于距離炸點(diǎn)2.45 m的同一水平面上。該信號為2008 年11 月于地下目標(biāo)毀傷技術(shù)國防重點(diǎn)學(xué)科實(shí)驗室中北大學(xué)爆炸塔處測得。

采用改進(jìn)的HHT 對該爆炸沖擊波信號進(jìn)行經(jīng)驗?zāi)B(tài)分解，選取相關(guān)系數(shù)最高的前10 組IMF 分量，并計算其能量分布時頻表示圖，結(jié)果如圖6、7 所示。

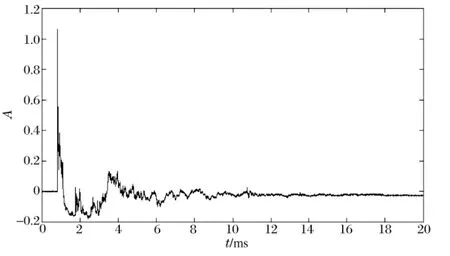
圖5 實(shí)測水中爆炸信號Fig.5 Experimental underwater explosion shock signal

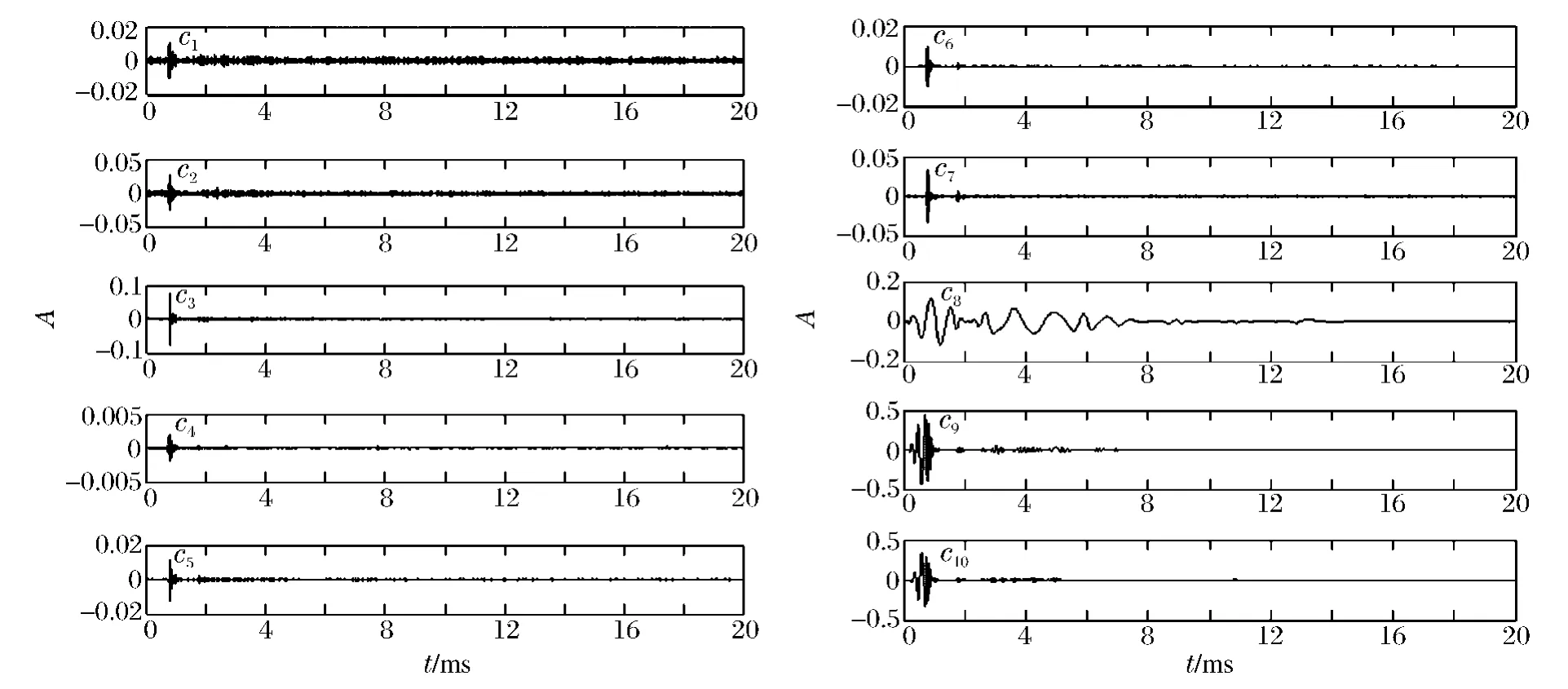
圖6 實(shí)測水中爆炸信號IMF 分量Fig.6 IMF components of experimental underwater explosion signal

圖7 實(shí)測水中爆炸沖擊波信號的HHT 能量分布譜時頻表示Fig.7 HHT time-frequency representation of experimental explosion shock wave using improved HHT

從圖6 可以看出，采用改進(jìn)的HHT 可以有效地得出爆炸沖擊波信號中感興趣的IMF 分量，低頻的IMF 分量通過相關(guān)系數(shù)篩選法被去除，僅僅保留了在爆炸沖擊波信號中的高頻信號;另外，由于在HHT之前先進(jìn)行了小波分解，這樣高頻處的第1 級固有模態(tài)函數(shù)IMF 分量c1的頻帶寬度被降低，解決了原始EMD 分解第1 級IMF 分量頻帶過寬的問題，使得生成的信號能量分布時頻表示更為精確有效。在圖7的能量分布圖中，采用改進(jìn)的HHT，爆炸沖擊波信號的高頻部分被更好地反映(如圖7 中5 ms 處的時頻分布)，由于沒有低頻IMF 分量以及相鄰IMF 分量之間的干擾，信號的時頻分布圖為進(jìn)一步的炸點(diǎn)定位、爆炸識別等奠定了更有效的基礎(chǔ)。

3 結(jié) 論

利用HHT 變換處理非平穩(wěn)信號的優(yōu)勢，結(jié)合小波分解及相關(guān)系數(shù)篩選法對水中爆炸信號進(jìn)行處理。結(jié)果表明，該方法能夠有效、準(zhǔn)確地分析爆炸沖擊波信號的時頻信息，得到爆炸信號能量分布的時頻圖，為進(jìn)一步對爆炸信號進(jìn)行時延估計、效能分析處理等提供了依據(jù)。但如果數(shù)據(jù)量較大時，在EMD進(jìn)行分解并得出HHT 時頻分布圖時需要很多時間，因此提高算法的速率將是進(jìn)一步研究的關(guān)鍵。

［1］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London.Series A:Mathematical，Physical and Engineering Sciences，1998，454(1971):903-995.

［2］ 賴思邈，張效民，曹丕.HHT 在水下目標(biāo)信號特征提取中的應(yīng)用［J］.電聲技術(shù)，2009，33(6):36-40.LAI Si-miao，ZHANG Xiao-min，CAO Pi.Application of HHT in feature extraction of underwater target signal［J］.Audio Engineering，2009，33(6):36-40.

［3］ 宋敬利，賈則，張姝紅.希爾伯特-黃變換在艦船沖擊響應(yīng)分析中的應(yīng)用［J］.水雷戰(zhàn)與艦船防護(hù)，2009，17(3):11-15.SONG Jing-li，JIA Ze，ZHANG Shu-hong.Hilbert-Huang transform and its applications on analysis of ships’shock response［J］.Mine Warfare＆Ship Self-Defence，2009，17(3):11-15.

［4］ Penga Z K，Tseb P W，Chua F L.An improved Hilbert-Huang transform and its application in vibration signal analysis［J］.Journal of Sound and Vibration，2005(286):187-205.