輪式車輛速差轉向過程的轉向阻力特性

李雪原，張宇，胡紀濱，苑士華

(北京理工大學 車輛傳動國家重點實驗室，北京100081)

0 引言

近幾年國內外出現了多種采用速差轉向的軍用或民用輪式車輛［1］。這些車輛通過主動改變兩側車輪的轉速實現轉向，可實現原地轉向與零半徑轉向，對比傳統幾何轉向的輪式車輛具備更好的轉向靈活性。關于此種車輛動力學的研究工作在國內外罕見報道。由于缺乏有針對性的設計理論，目前只能簡單套用履帶車輛轉向理論。因此，開展速差轉向車輛動力學研究工作已經成為一項緊迫而重要的工作。

進行速差轉向車輛動力學研究的前提是要對速差轉向過程中輪胎與地面相互作用的力學特性有較為深入的認識。本文針對某采用速差轉向的全地形車在軟路面上進行轉向時的輪胎－地面力學特性進行研究，建立適合此種工況下的宏觀力學模型，并利用離散單元仿真軟件PFC2D 進行仿真。

1 輪胎－地面相互作用宏觀力學分析

人們對履帶式車輛作速差轉向研究作了大量工作［2］，履帶式車輛作速差轉向時，地面橫向阻力的計算主要基于以下假設:坦克法向載荷沿履帶接地段均勻分布，即載荷分布為矩形［3］如圖1所示。地面轉向阻力Fy和法向載荷G 成正比，轉向阻力系數

但是，這種假設條件對于輪式車輛卻不能成立。在輪荷較低時，輪式車輛各輪胎上的載荷分布如圖1所示［4］。對應的轉向時輪胎印跡上轉向阻力的分布如圖2所示［5］。

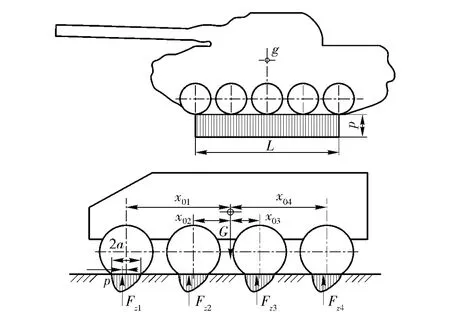
圖1 履帶車輛與輪式車輛的法向載荷分布Fig.1 Normal load distribution of tract and wheeled vehicles

由圖2可知，車輛在水平地面上、低速、勻速、單車轉向時，轉向中心前后輪胎上的轉向阻力方向相反，側向力Fyij是平衡的:

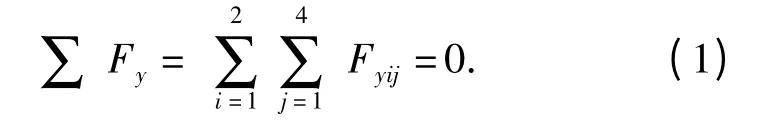
車輛在水平地面上轉向時，所受的縱向力和側向力(轉向阻力)對車輛平面中心C 點取矩，就形成了轉向時的2 個外力矩，這就是車輛的轉向驅動力矩和地面轉向阻力矩。

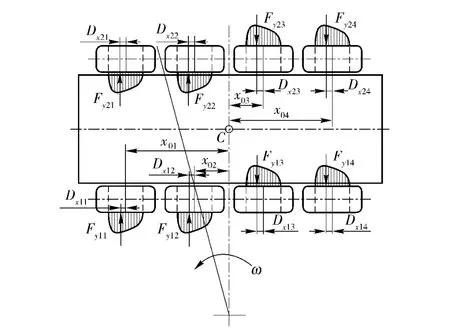
圖2 輪式車輛轉向阻力分布Fig.2 Steering resistance distribution of wheeled vehicle

轉向時地面的轉向阻力矩Tz主要是地面轉向阻力Fyij所造成的。由圖2可知，地面轉向阻力與坦克平面中心C 點的距離為(x0j+ Dxij)，j =1，2 或(x0j－Dxij)，j =3，4，其中Dxij為輪胎(編號ij)的拖距，將轉向阻力對平面中心C 點取矩，可得地面轉向阻力矩公式:

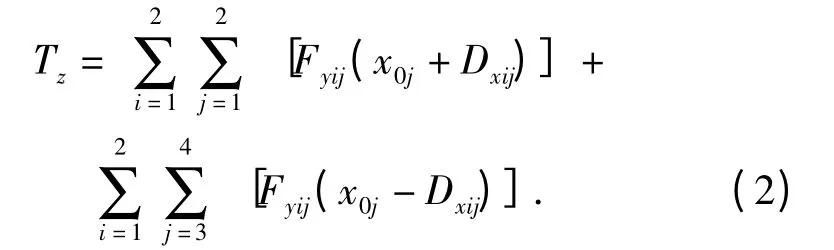
由(2)式可知，地面轉向阻力矩純粹是地面的橫向阻抗力矩，隨車重、車軸之間的距離、地面轉向阻力系數的增加而增加。車軸之間的距離過長會造成轉向阻力矩增大，不利于整車的轉向性能。

定義單個輪胎的轉向阻力系數

式中:μij為第ij 輪的轉向阻力系數;Fyij為第ij 輪的側向阻力;Fzij為第ij 輪的輪荷。

輪胎的轉向阻力系數表示輪胎所受轉向阻力與輪荷的關系，便于在后續的工作中更好的描述轉向過程中輪胎的工作狀態。

2 地面離散單元模型

離散單元法(DEM)的基本思想是把介質看作由一系列離散的獨立運動的單元所組成，單元的尺寸是細觀的，利用牛頓第二定律建立每個單元的運動方程，并用顯式中心差分法求解，整個介質的變形和演化由各單元的運動和相互位置來描述［6］。

2.1 線性接觸剛度模型

線性接觸剛度模型是離散單元法的基本理論模型如圖3所示:Fn為法向接觸力，Ft為切向接觸力，Fc為接觸合力，變形發生在接觸點處。使用力－位移接觸定律可計算2 個顆粒相互作用的接觸力［7］

“經過一年多來的共建，構建‘西江水上安全命運共同體’倡議獲得廣泛共識，政府、企業、社會‘三位一體’的水上安全治理架構正不斷完善。”陳畢伍表示。

式中:kn為法向接觸剛度;Un為法向接觸位移。

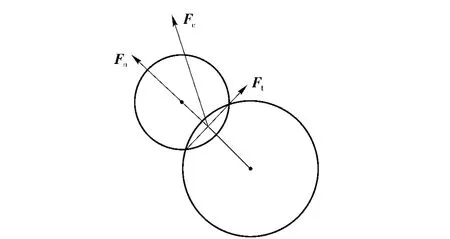
圖3 線性接觸剛度模型Fig.3 Linear contact stiffness model

切向接觸力以增量的形式計算。同樣應用力－位移接觸定律得到2 個顆粒相互作用時的切向接觸力增量

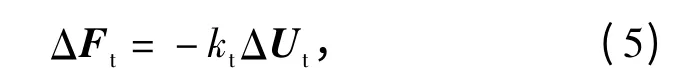
式中:ΔFt為切向接觸力增量;kt為切向接觸剛度;ΔUt為相對切向位移增量。

在線性接觸剛度模型中，假定2 個接觸顆粒的剛度串聯作用，所以法向接觸剛度kn和切向接觸剛度kt計算公式［7］為:

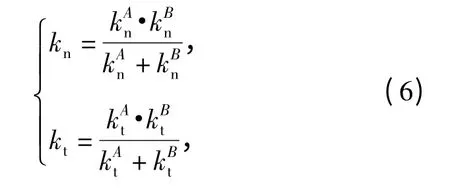
式中:kAn為顆粒A 的法向接觸剛度;kBn為顆粒B 的法向接觸剛度;kAt為顆粒A 的切向接觸剛度;kBt 為顆粒B 的切向接觸剛度。

2.2 滑移模型

滑移模型能夠合理描述土壤顆粒在接觸點處的本構關系，是2 個接觸顆粒的一個固有屬性。它沒有法向抗拉強度，通過限制切向力來允許顆粒在抗剪強度范圍內發生滑移［8］。

滑移模型通過接觸處的摩擦系數μ 來確定。μ 為2 個相互接觸顆粒之間摩擦系數的最小值。最大允許切向接觸力由(7)式確定，當切向接觸力等于最大允許切向接觸力時，則在進行下一步計算時認為顆粒之間發生滑移［9］。

式中:Ftmax為最大允許切向接觸力;μ 為接觸處的摩擦系數，取2 個接觸顆粒摩擦系數的最小值。

2.3 并行約束模型

顆粒流程序允許使用并行約束將顆粒在接觸的位置約束在一起。并行約束描述了2 個顆粒之間的粘性物質的本構特性［9］。并行約束在顆粒之間建立了一種彈性相互關系，這種關系可與以上介紹的滑移模型并行作用。由于離散顆粒為厚度t 的彈性圓盤，故一個并行約束可看作一系列具有恒定法向和切向剛度的彈性彈簧，這些彈簧均勻分布在接觸點為中心的接觸平面的矩形橫截面上，它們與描述線性接觸剛度模型的點接觸彈簧并行作用，并行約束模型如圖4所示，右側圖是左側圖中矩形框的放大。圖中，Fpnb為并行約束法向分力;Fptb為并行約束切向分力;M3pb為并行約束合力矩。

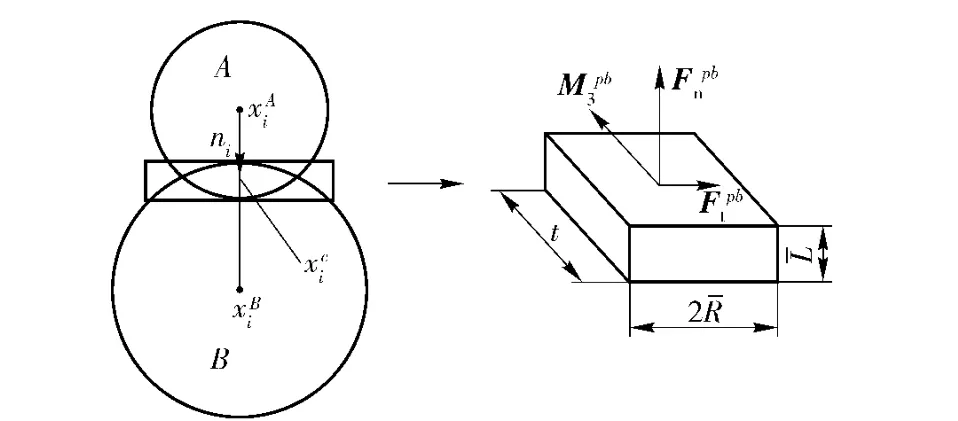
圖4 并行約束模型Fig.4 Parallel－bond model

使用并行約束模型的顆粒在接觸點處相對運動時，并行約束剛度的影響會在并行約束物質內部產生力和力矩。這些力和力矩作用在2 個顆粒上，且與作用在約束物質內部的最大法向和切向應力有關。如果這2 個最大應力之一超過對應的約束強度時，并行約束發生斷裂［9］。

3 輪胎－地面相互作用仿真分析

3.1 輪胎－地面側向作用模型的建立

PFC2D 是由ITASCA 公司開發的顆粒流分析程序，適用于分析二維離散單元集合體運行及其相互作用［9］。為簡化研究過程，在軟件中將土壤顆粒集合體的宏觀尺寸和土槽的尺寸設置相同大小。模擬土槽墻由幾個標準墻生成，土壤顆粒在以墻為邊界的區域內生成。考慮離散元模擬土壤顆粒的大小和模擬的計算效率，以及土槽尺寸對模擬土壤動態行為變化規律的影響，選取土槽的長750 mm，深250 mm，土壤顆粒數量為16 500.對于不同性質的土壤模型的仿真，可通過改寫土壤參數實現。

在輪胎側面作用下土壤動態行為分析時，重點研究輪胎側面土壤擠壓、爬升、拱起等動態行為變化規律，所以將輪胎簡化為剛性墻，忽略其在此過程中出現的扭曲、斜切等彈性變形。建立多層土壤，以便清晰再現不同位置干土壤顆粒的滑移、錯動等離散元細觀動態行為變化。在土壤動態行為離散元細觀模擬過程中，根據輪胎側面的下陷深度、土壤動態行為重點考察區域等將整個土槽劃分為2 層顏色不同但性質相同的區域。2 層區域的厚度與模擬土槽的深度相同，長度分別設定為50 mm、100 mm.

某型全地形車所用輪胎型號為AT27 ×12R14，根據其幾何參數使用PFC2D 軟件建立輪胎－地面相互作用模型，如圖5所示。

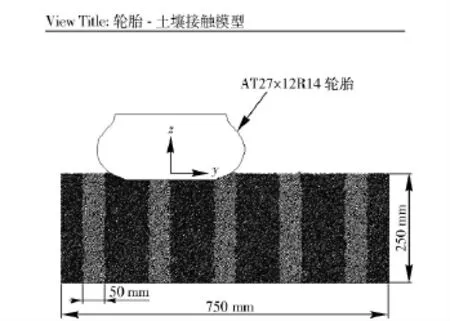
圖5 輪胎－地面側向離散元細觀仿真模型Fig.5 Tire－ground lateral interaction micromechanical model

3.2 不同性質土壤的側向推土阻力及摩擦力分析

設置仿真步長0.001 s，分別考慮輪胎在砂性土壤和粘性土壤路面的運動狀況。輪胎相對滑動速度vr為0.05 m/s，下陷量z 為15 mm，仿真結果如圖6所示。

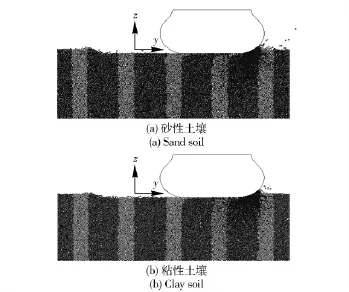
圖6 輪胎側向滑動仿真結果Fig.6 Simulation results of the tire lateral sliding

圖7 輪胎－土壤顆粒接觸力場Fig.7 Tire－soil particles contract stress field

相對滑動速度vr為0.05m/s，下陷量z 為15 mm時，輪胎在砂性土壤和粘性土壤上作橫向運動時產生的側向推土阻力Fyv及摩擦力Fyf的變化情況如圖8所示。

3.3 單一性質土壤在輪胎處于不同滑移速度和下陷深度時側向推土阻力及摩擦力分析

對于某一特定性質的路面，輪胎處于不同工作狀態時，路面與輪胎之間的側向推土阻力及摩擦力也會不同。考慮輪胎相對滑動速度vr為0.05～0.20 m/s，下陷量z 為5～20 mm，路面采用砂性土壤。仿真結果如表1～2 所示。

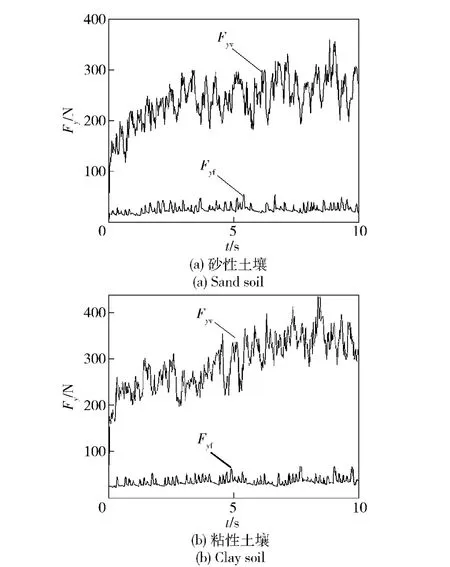
圖8 側向推土阻力及摩擦力Fig.8 The lateral bulldozing resistance and friction force

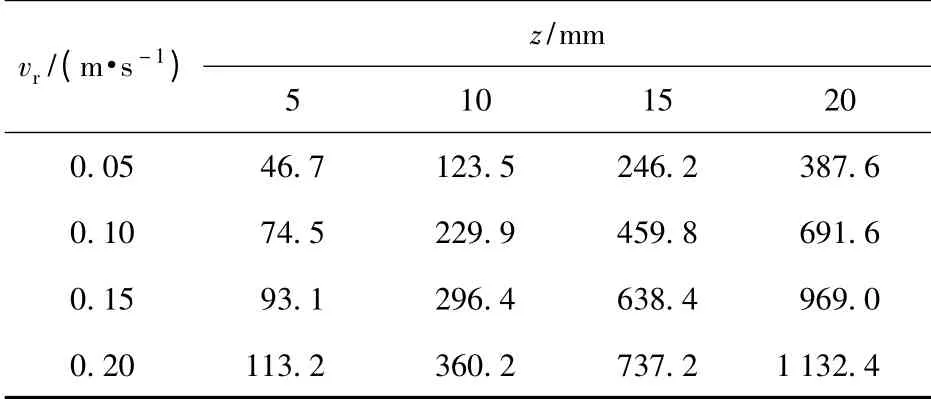
表1 砂性土壤推土阻力仿真結果Tab.1 Simulation results of the bulldozing resistance of sand soil N

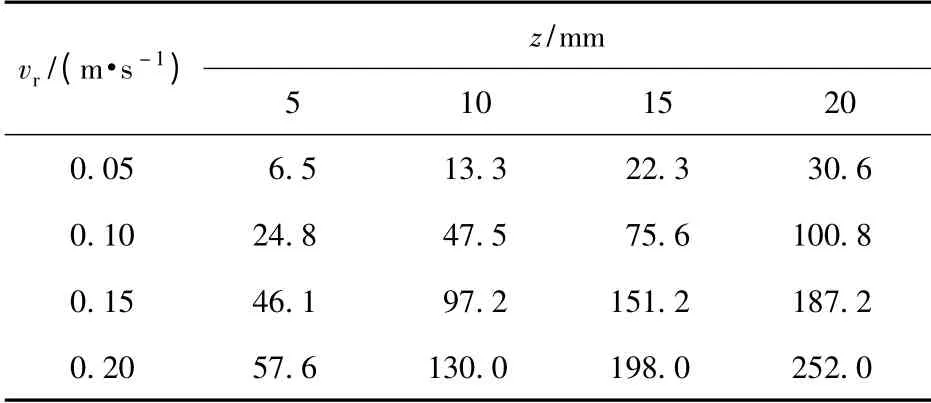
表2 砂性土壤摩擦力仿真結果Tab.2 Simulation results of the friction force of sand soilN

使用最小二乘法擬合仿真所得數據，選取形如Fy=azbvcr的擬合公式，可得適用于砂性土壤的側向推土阻力及摩擦力的經驗公式，如(8)式所示:

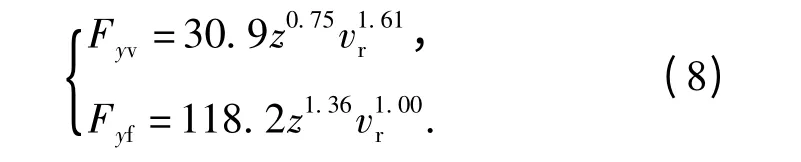
(8)式反映了在砂性路面上輪胎處于不同的滑移速度和下陷深度時所受的側向推土阻力及摩擦力的關系，2 者的圖像如圖9所示。

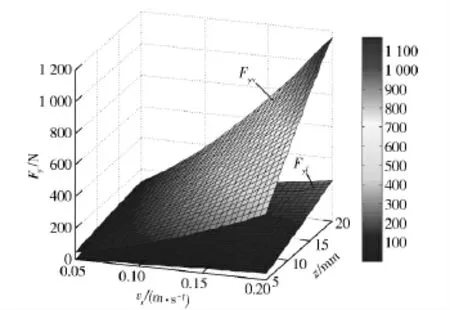
圖9 側向推土阻力及摩擦力與滑移速度、下陷深度的關系Fig.9 Relationship of resistance－relative slip velocity and resistance－sag depth

輪胎側向運動時的總側向阻力由下式計算

再由(3)式可得到轉向時此輪胎與路面相互作用時的轉向阻力系數μi，可得到如(10)式所示的擬合公式:

在砂性土壤轉向時的μi圖像如圖10 所示。

4 結論

輪式車輛在地面上轉向過程中，對地面的正壓力產生了摩擦阻力，由于正壓力同時造成了地面的沉降，還產生了推土阻力。本文利用離散單元法分析輪式車輛在速差轉向過程中的轉向阻力。給出了對于特定路面的側向推土阻力、側向摩擦力以及輪胎轉向阻力系數的擬合公式。本文的主要結論如下:

1)輪胎在粘性土壤上運動阻力是砂性土壤上的1.2～1.4 倍。在粘性土壤和砂性土壤上側向運動時，側向推土阻力大約是輪胎胎面與地面的側向摩擦力的5～8 倍。

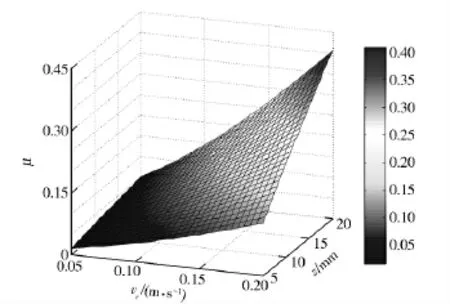
圖10 轉向阻力系數與滑移速度、下陷深度的關系Fig.10 Relationship between the steering resistance coefficient and slip velocity，sag depth

2)在砂性土壤上，隨著滑移速度的增大，側向推土阻力和側向摩擦力也增大。側向推土阻力與側向摩擦力的比值仍是5～8 倍。

3)輪胎轉向阻力系數隨著滑移速度和下陷深度的增加而發生顯著變化，在特定的砂性土壤上，輪胎的轉向阻力系數μi由(10)式給出。

References)

［1］ 金曉輝，宋永剛，何建清.輕型全地形車現狀及發展趨勢分析［J］.汽車運用，2005，(7):15－16.JIN Xiao－hui，SONG Yong－gang，HE Jian－qing.Investigation and development trends of light ATV［J］.Auto Application，2005，(7):15－16.(in Chinese)

［2］ Bruce M.A skid steering model with track pad flexibility［J］.Journal of Terramechanics，2007，44(1):95－100.

［3］ 閆清東，張連第，趙毓芹.坦克構造與設計(下冊)［M］.北京:北京理工大學出版社，2007:224－226.YAN Qing－dong，ZHANG Lian－di，ZHAO Yu－qin.Structure and design of tanks (B)［M］.Beijing:Beijing Institute of Technology Press，2007:224－226.(in Chinese)

［4］ 莊繼德.汽車輪胎學［M］.北京:北京理工大學出版社，1996:134－138.ZHUANG Ji－de.Automobile tire［M］.Beijing:Beijing Institute of Technology Press，1996:134－138.(in Chinese)

［5］ 郭孔輝.輪胎側偏特性的一般理論模型［J］.汽車工程，1990，12(3):1－12.GUO Kong－hui.A generalized analysis for tire side－slip characteristics［J］.Automotive Engineering，1990，12(3):1－12.(in Chinese)

［6］ Bernhard P，Algis D I.Numerical simulation of the motion of granular material using object－oriented techniques［J］.Computer Methods in Applied Mechanics and Engineering，2002，191(17－18):1983－2007.

［7］ Cundall P A，Satake M，Jenkins J T，et al.Computer simulations of dense sphere assemblies in micromechanics of granular materials［M］.Amsterdam:Elsevier Science Publishers，1988:113－123.

［8］ Mindlin R D，Deresiewicz H.Elastic spheres in contact under varying oblique forces［J］.Journal of Applied Mechanics，1953，20:327－344.

［9］ Cundall P A，Strack O D L.Particle flow code in 2 dimensions［M］.New York:Itasca Consulting Group Inc，2004.