上海市天然氣銷售量的ARMA模型

上海市燃氣調度中心 任楨

1 模型綜述

ARMA(Auto-Regressive and Moving Average Model)自回歸移動平均模型是研究時間序列的重要方法，也稱博克斯詹金斯(B-J)法，常用于精度較高的時序短期預測，或者具有季節變動特征的銷售量、市場規模的預測。ARMA（p,q）模型表示為：

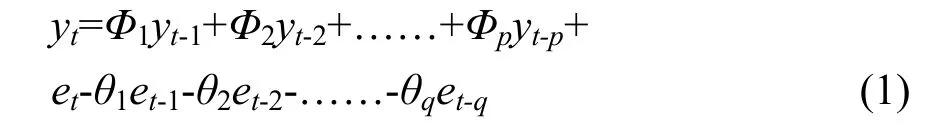
式中：yt—當期預測值(t=1，2，…，T)；

p—自回歸階數；

q—移動平均階數；

Φi—模型的待定系數(i=1，2，…，p)；

θj型的待定系數(j=,2,……q)；

et—誤差(t=1，2，…，T)。

特殊情況：q=0，模型即為AR(p)自回歸模型，p=0，模型即為MA(q)移動平均模型。

影響天然氣銷售的因素有很多，從成分劃分有居民消費用氣，電廠消費用氣，工業用氣，化工用氣，從客觀因素劃分有季節性變動，氣溫氣候變動，節假日變動，工作日和非工作日變動，生活習慣改變，經濟景氣情況，人工煤氣置換進度等等。影響因素錯綜復雜，分析和預測較為困難，所以本文運用 ARMA模型通過天然氣月銷售量進行分析，找出其規律，進行運用。

2 數據來源

本文的數據來源于上海市燃氣調度中心燃氣調度系統上海燃氣供應輸配儲存情況日報(2006年 1月~2011年5月)天然氣月度銷售累計值，見表1。

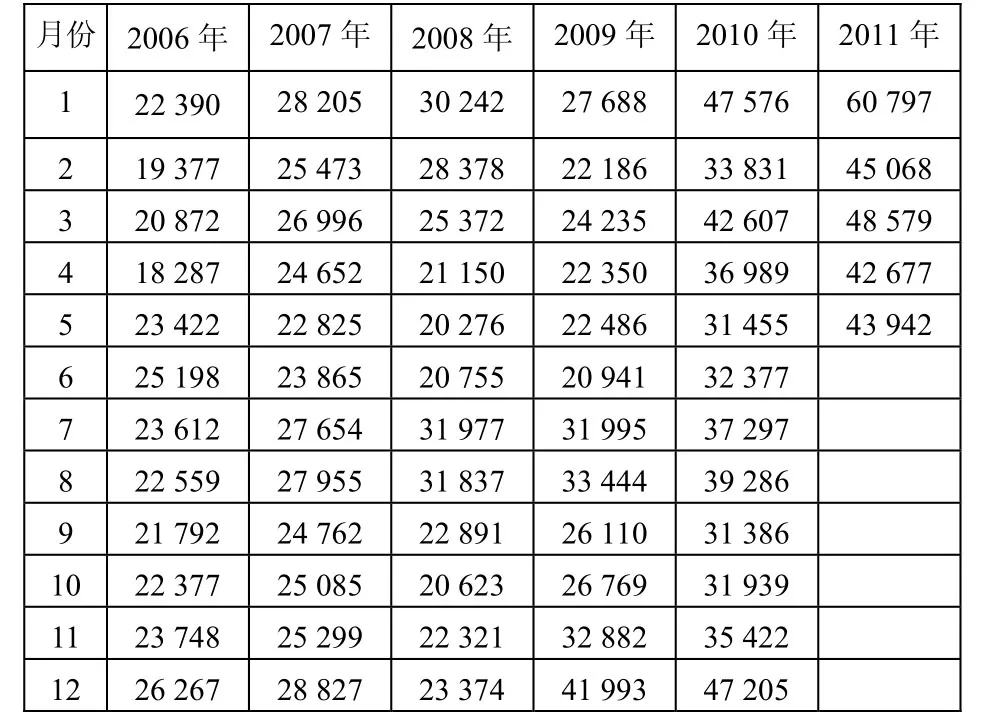
表1 上海市天然氣月銷售量單位：萬m3

用Eviews軟件作時序分析，可得圖1所示趨勢圖。

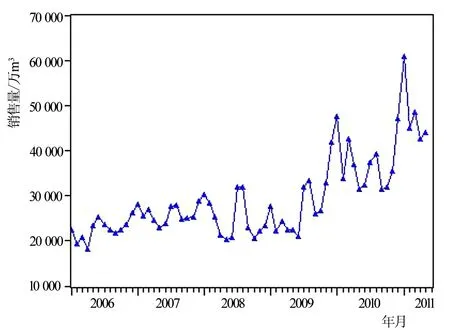
圖1 上海市天然氣月銷售量銷售量趨勢

由圖 1可見天然氣月銷售量的周期季節性變動，并且2009年后有較快增長趨勢。由表1和圖1可知該序列是非平穩序列，又因為時間序列模型是建立在隨機序列平穩性的基礎上的。

因此對原序列進行1階差分零均值處理，獲取零均值平穩性序列。公式為：

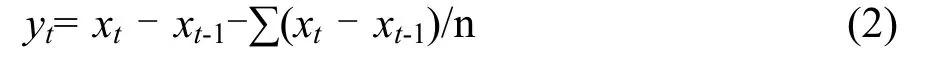
式中：xt為原序列，xt- xt-1為原序列1階差分項，∑(xt- xt-1)/n為原序列平均數。

生成新序列定義為y，采用ADF單位根檢驗法，進行平穩性檢驗，見圖2，ADF的統計量分別小于不同顯著性水平的三個檢驗臨界值，所以序列y通過了ADF檢驗，認為該序列是平穩的。

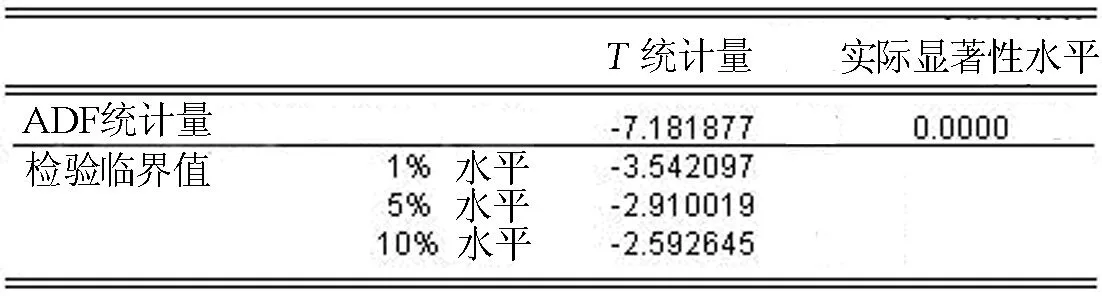
圖2 ADF統計量檢驗

3 模型建立

建立ARMA模型，需要確定p，q數值各是多少，為此需要利用軟件 Eviews來計算自相關系數和偏自相關系數。

從一階相關系數圖3可以看出自相關系數在滯后階數為12時顯著不為0，在滯后階數大于12時基本處于置信帶內，所以可取q=12，偏自相關系數在滯后階數為12時顯著不為0，可取p=12。

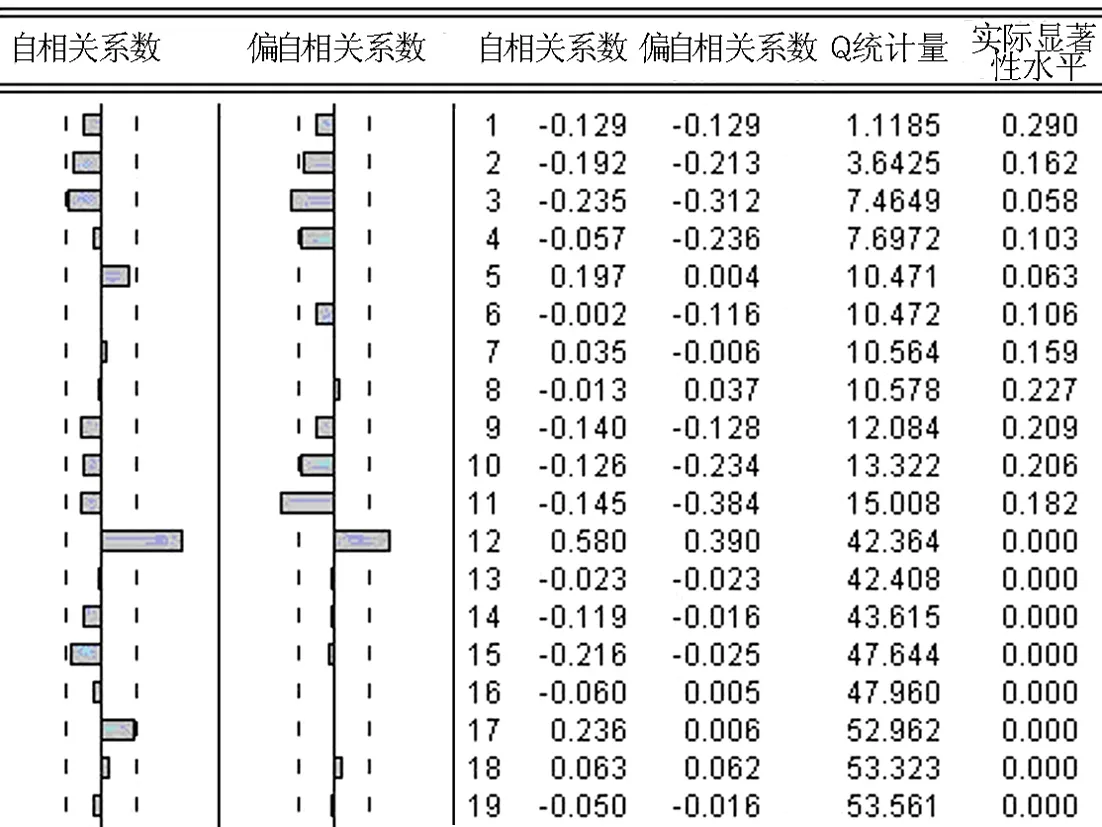
圖3 一階差分相關系數

由于可能有多個適應性模型，通常根據輸出項的赤池準則(AIC)和施瓦茨準則(SC)進行比較，兩個統計量值越小越好，經比較，采用 ARMA(12,12)模型。

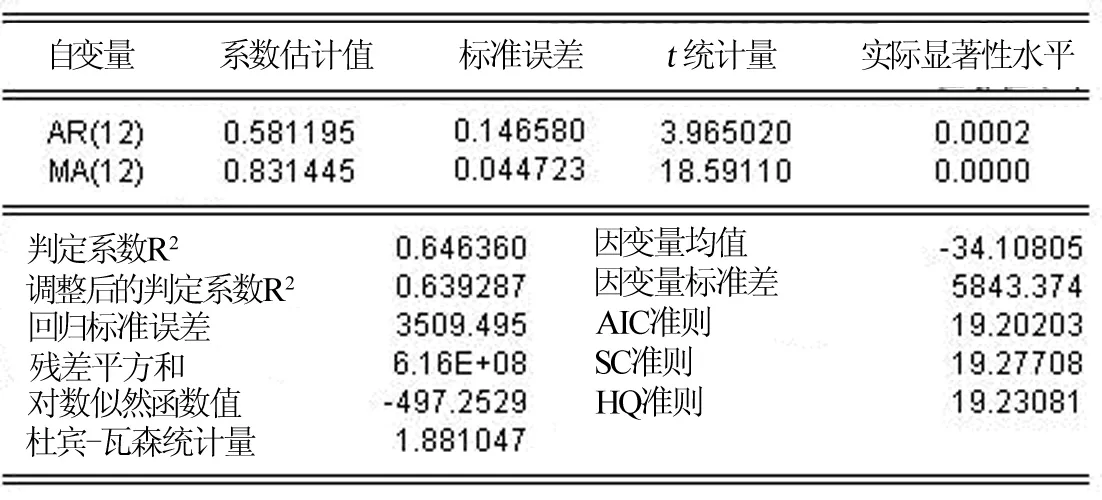
圖4 ARMA(12,12)模型

此模型的AR和MA的特征方程的特征根的絕對值均小于 1，所以該模型是平穩的，可逆的。此外ARMA(12,12)模型的AIC(Akailke info criterion)和SC(Schwarz criterion)統計量值相對最小。

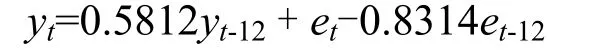
對模型的殘差et序列的進行自相關和偏相關圖分析確認不存在有用信息，如圖5所示。

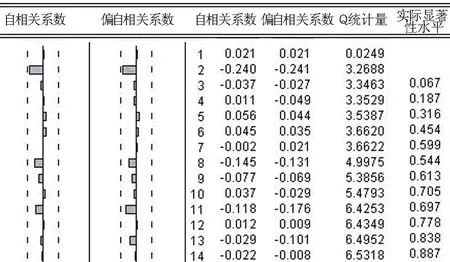
圖5 殘差序列的相關系數

由圖5殘差序列的Q統計量進行白噪聲檢驗，可知該殘差序列相互獨立，白噪聲概率很大，即該序列不存在有用的信息未提取，所以接受該模型。

4 模型運用

最終確定是ARIMA(12,1,12)模型，模型說明該序列有12階自回歸過程，即當前值與滯后12期的觀測值有線性關系，此外也受到滯后 12期殘差項的影響。

運用EViews軟件分別預測檢驗3、4、5月銷售量為51 834.2萬m3，41 070.5萬m3，37 108.4萬m3相對誤差分別為6.3%，-3.9%，-18.4%。

因5月份銷售量中電廠用量為14 147.1萬m3環比增加24.6%，同比增加60.4%；與4月份電廠環比增加19.3%，同比增加35.7%，相對增加很快，故而造成了模型預測值誤差較大。

因此本模型只適用于外部環境沒有大的改變情況下的短期預測。

5 結論

綜上所述，可以運用EViews等統計軟件來建立非平穩時間序列的 ARMA模型，對上海市天然氣月銷售量進行短期預測研究。以此類推，也可以建立天然氣直供量，人工煤氣，月度或者年度ARMA模型用以研究。