CA砂漿彈模對框架板式軌道翹曲應力的影響分析
周 毅,何燕平,楊榮山
(西南交通大學 土木工程學院,成都 610031)
CA砂漿彈模對框架板式軌道翹曲應力的影響分析
周 毅,何燕平,楊榮山
(西南交通大學 土木工程學院,成都 610031)
采用有限元分析法,對框架板在溫度梯度作用下的翹曲應力進行仿真計算,分析了砂漿彈性模量的變化對框架板溫度效應的影響。結果表明:在溫度荷載作用下,框架板式軌道框架角點處和凸臺邊緣處將產生局部翹曲應力的集中,最大的翹曲應力產生在軌道板角點處,并產生最大的翹曲位移;隨著CA砂漿彈模的增加,軌道板應力集中區域的最大翹曲應力逐漸減小,軌道板角點翹曲位移也逐漸減小。
框架板式軌道 翹曲應力 CA砂漿 有限元法
溫度對無砟軌道結構的影響十分明顯,軌道板的溫度主要指兩個方面:一是軌道板整體的溫度升降,這使軌道板發生整體的伸縮;二是軌道板沿其高度方向的溫度遞變即溫度梯度,這是軌道板發生翹曲、表層開裂和板底分離的主要原因。為研究CA砂漿層對框架板式軌道翹曲應力的影響,利用ANSYS有限元軟件,分析了砂漿彈性模量的變化對框架板溫度效應的影響,為無砟軌道的結構設計提供依據。
1 翹曲應力計算基本理論
當物體內部存在溫度差,即存在溫度梯度時,熱量會從物體的高溫部分傳遞到低溫部分;兩個不同溫度的物體相互接觸時,熱量會從高溫物體傳遞到低溫物體,熱傳導遵循傅立葉定律

式中 q″——熱流密度;
k——導熱系數或熱傳導率。
式(1)中負號表示熱量流向溫度降低的方向。當溫度T沿混凝土板厚度x不均勻分布時,板內產生翹曲變形。板頂溫度高于板底溫度時,板頂面纖維的伸長變形大于底面纖維,板中部便出現向上拱起。而在板頂溫度低于板底溫度時,板頂面纖維的收縮變形大于底面纖維,板四邊出現向上翹起。
2 計算模型與計算參數
溫度翹曲應力分為“上熱下冷”和“上冷下熱”兩種,兩種情況在板厚方向的溫度梯度均按0.5℃/cm線性變化進行計算。考慮到主要分析CA砂漿彈模對軌道板翹曲應力的影響,故只選擇“上熱下冷”的情況作為分析對象。在計算模型中,軌道板、CA砂漿層、混凝土底座以及凸形擋臺均采用實體單元進行模擬。模型中將軌道板分層,并“由上至下”按照線性變化的方式賦于不同的溫度荷載,且保證施加溫度荷載之和為0。模型中認為砂漿與軌道板以及混凝土底座板的接觸是一種完全密貼的全支承狀態,故在處理軌道板、混凝土底座板和砂漿的接觸條件時,采用粘接方式進行模擬,保證接觸面間的位移一致。計算模型如圖1所示,計算參數如表1所示。
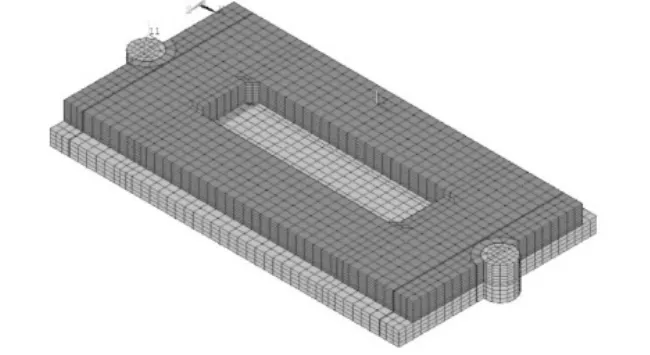
圖1 框架板式軌道有限元模型

表1 計算參數
3 計算結果及分析
3.1 翹曲應力和翹曲位移計算
保證其它參數不變,改變CA砂漿層彈性模量,分別計算框架軌道板溫度翹曲應力和翹曲位移。計算云圖如圖2~圖4所示。

圖2 橫向翹曲應力分布
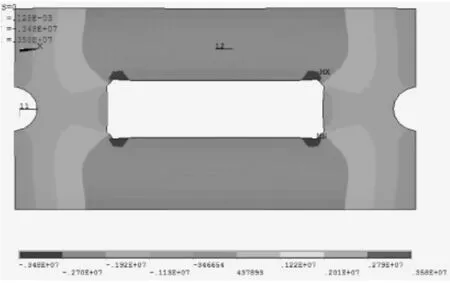
圖3 縱向應力分布

圖4 翹曲位移分布
由圖2~圖4可知,在凸臺邊緣和框架角點處,會發生縱向翹曲應力集中,在凸臺邊緣與框架邊緣之間產生較大的縱向翹曲應力;橫向翹曲應力集中發生在框架角點處,在框架邊緣與軌道板邊緣之間將產生較大的橫向應力。在應力集中處,將產生最大的翹曲應力,在軌道板角點處將產生最大的負向翹曲位移,在框架邊緣與軌道板邊緣之間、凸臺邊緣與框架邊緣之間軌道板將產生一定的上拱變形。不同砂漿彈模下軌道板的最大翹曲應力和翹曲位移如表2所示。

表2 不同CA砂漿彈模下的計算結果匯總
由表2可知,框架軌道板的縱橫向最大翹曲應力均隨著CA砂漿彈模的增加而減小,橫向應力略大于縱向應力,隨著CA砂漿彈模的增加,橫向應力與縱向應力的差值逐漸縮小。翹曲位移則隨著CA砂漿彈模的增加而減小。說明增加CA砂漿彈模可減小軌道板的最大翹曲應力和最大翹曲位移。
3.2 翹曲應力和翹曲位移分布規律研究
根據在不同CA砂漿彈模情況下,計算出的框架板各處的翹曲應力和翹曲位移,分析翹曲應力和翹曲位移隨CA砂漿彈模的分布變化的規律。對比分析位置見圖5。位置1主要分析軌道板縱向上翹曲應力隨砂漿彈模變化的分布規律;位置2主要分析軌道板橫向上翹曲應力隨砂漿彈模變化的分布規律;位置3主要分析軌道板縱向上翹曲位移隨砂漿彈模變化的分布規律;位置4主要分析軌道板橫向上翹曲位移隨砂漿彈模變化的分布規律。不同CA砂漿彈模下各位置的翹曲應力和翹曲位移分布變化情況如圖6~圖9所示。
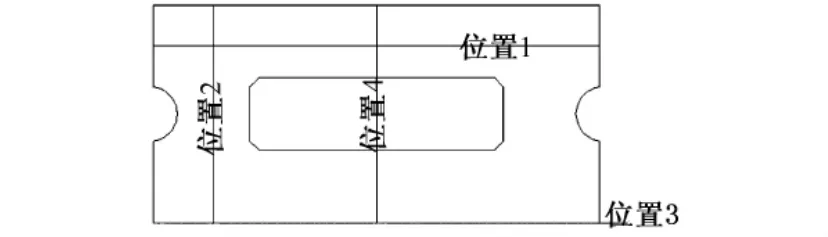
圖5 框架板翹曲應力、位移對比分析位置
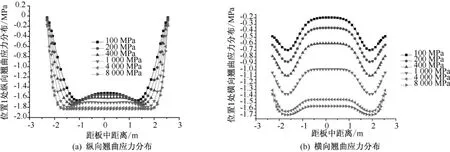
圖6 位置1處軌道板翹曲應力隨CA砂漿彈模變化的分布規律
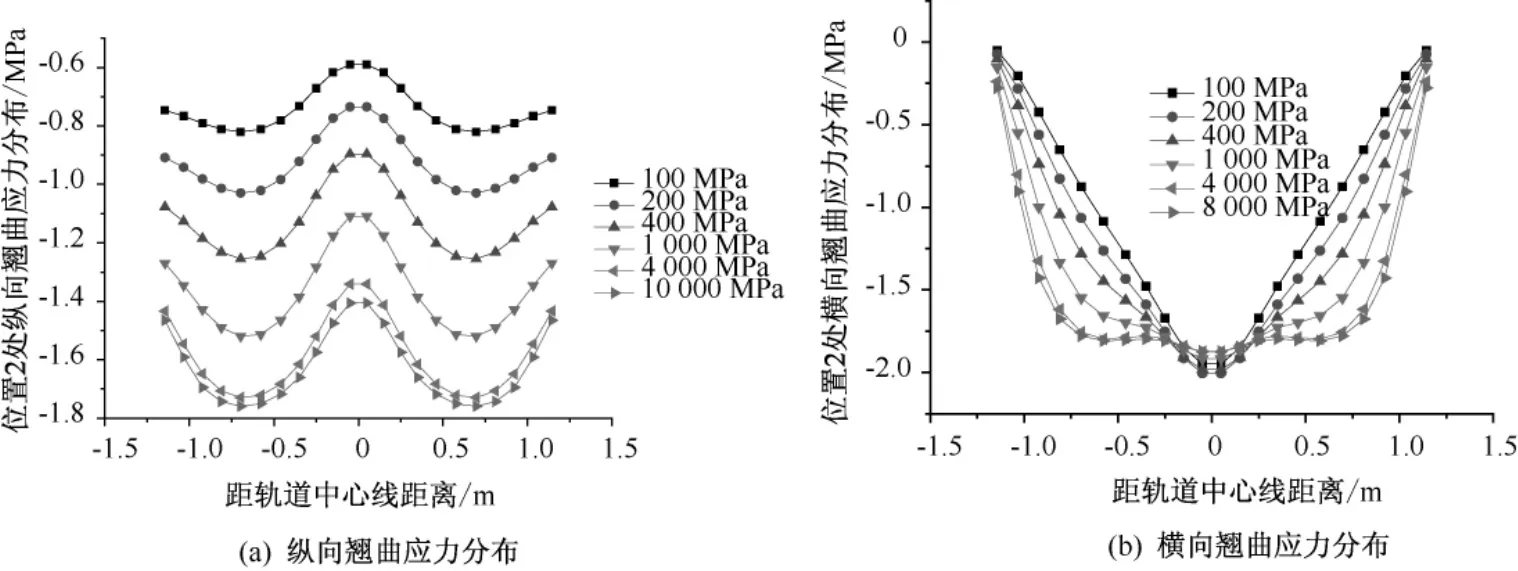
圖7 位置2處軌道板翹曲應力隨CA砂漿彈模變化的分布規律

圖8 位置3處框架板翹曲位移的分布規律
由圖6可知,在軌道板縱向上,軌道板縱橫向翹曲應力由軌道板邊緣向軌道板中心逐漸增大,在軌道板中心出現應力極值。隨著CA砂漿彈模的增加,位置1處的縱橫向最大翹曲應力逐漸增大,但翹曲應力由板邊向板中的變化幅度逐漸減緩。
由圖7可知,在軌道板橫向上,軌道板縱橫向翹曲應力由軌道板邊緣向軌道板中心逐漸增大,在軌道板中心出現應力極值。隨著CA砂漿彈模的增加,位置2處的橫向最大翹曲應力有所減小,橫向翹曲應力由板邊到板中的變化幅度逐漸減緩;位置2處的縱向最大翹曲應力逐漸增加,縱向翹曲應力由板邊到板中的變化幅度隨CA砂漿彈模的增加而有所增加。
由圖8和圖9可知,在軌道板縱橫向上,軌道板的最大翹曲位移均隨著CA砂漿彈模的增加而減小,且翹曲位移的分布隨著砂漿彈模的增加而趨于均勻。
4 結論
1)在溫度荷載作用下,框架板式軌道框架角點處和凸臺邊緣處將產生局部翹曲應力的集中,產生最大的翹曲應力,在軌道板角點處將產生最大的翹曲位移。隨著CA砂漿彈模的增加,軌道板應力集中區域的最大翹曲應力逐漸減小,軌道板角點翹曲位移也逐漸減小,其余部分的翹曲應力逐漸增大,翹曲應力以及翹曲位移由板邊向板中的變化幅度逐漸減小。
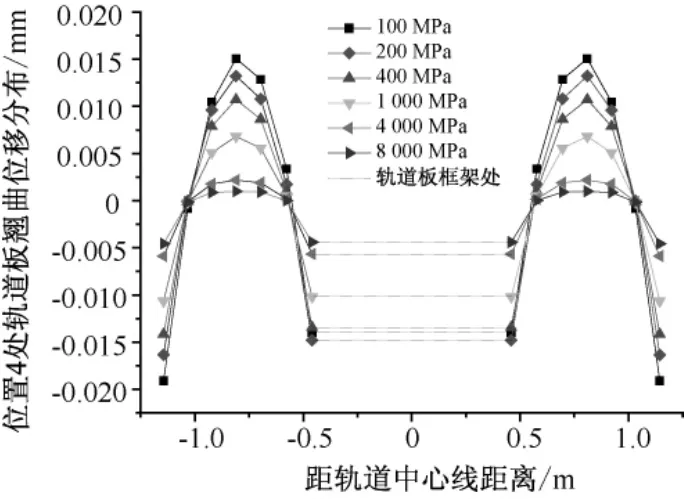
圖9 位置4處框架板翹曲位移的分布規律
2)在軌道板縱向上,增加CA砂漿的彈模,會增加軌道板的縱橫向翹曲應力,但可以減緩翹曲應力由板邊向板中的變化幅度。軌道板在縱向上的翹曲位移則隨著CA砂漿彈模的增加而減小,軌道板的翹曲位移在縱向上的分布也趨于均勻。
3)在軌道板橫向上,增加CA砂漿的彈模,會增加軌道板的縱向翹曲應力,增加縱向翹曲應力由板邊到板中的變化幅度;橫向翹曲應力與其變化幅度均隨著CA砂漿彈模的增加而有所減小。軌道板在橫向上的翹曲位移則隨著CA砂漿彈模的增加而減小,軌道板的翹曲位移由板邊到板中的變化幅度也逐漸減小。
[1]趙國堂.高速鐵路無碴軌道結構[M].北京:中國鐵道出版社,2006.
[2]石現峰.溫度對板式無砟軌道結構的影響研究[J].鐵道工程學報,2008(5):30-32.
[3]王森榮.無砟軌道軌道板溫度測量與溫度應力分析[J].鐵道工程學報,2009(2):52-55.
[4]王秋會.幾種特殊無砟軌道板的受力探討及仿真分析[J].鐵道標準設計,2009(增刊):7-9.
[5]高俊英.土質路基上CRTS-I型板溫度力分析[D].成都:西南交通大學,2008.
[6]王森榮.板式無砟軌道溫度力研究[D].成都:西南交通大學,2007.
[7]趙坪銳,劉學毅.連續道床板溫度應力計算方法及參數分析[J].鐵道建筑,2008(11):81-85.
U213.2+42
A
1003-1995(2011)03-0103-03
2010-10-02;
2010-12-26
周毅(1986— ),男,四川簡陽人,碩士研究生。
(責任審編 王 紅)

