POS數據的上下視差誤差源檢測及誤差補償回歸模型

張永軍,熊金鑫,熊小東,鄧繼偉

1.武漢大學遙感信息工程學院,湖北武漢430079;2.鐵道第三勘察設計院集團有限公司,天津300251

1 引 言

快速而且正確地恢復攝影時刻像片的空間方位是航空攝影測量的關鍵技術之一。長期以來,這一目標是通過空中三角測量方法借助大量的地面控制點間接實現。隨著傳感器技術、空間定位技術和計算機技術的發展,航空攝影測量理論越來越嚴密、方法越來越先進[1]、所需地面控制點越來越少,正朝著無地面控制的方向發展[2]。

20世紀70年代以后,美國研制成功了新一代衛星無線電導航系統——全球定位系統(GPS),由于它能進行高動態精密三維定位,并可用于在航空攝影的同時確定像片的外方位元素,從而引起了攝影測量界的極大興趣和普遍關注[3]。在20世紀末出現的定位定向系統(position and orientation system,POS)集差分GPS技術和慣性導航(INS)技術于一體,可在航空攝影時獲取航攝像片的6個外方位元素[4],直接用于航空攝影測量影像的定向[5]。已有試驗表明,利用POS系統獲取的像片外方位元素可以直接制作數字正射影像圖[6],而對地形測圖而言由于POS系統誤差尤其是視準軸誤差的存在[7],直接將POS提供的像片外方位元素用于安置元素測圖[8]會產生作業員無法忍受的模型上下視差。

本文根據基于POS的相對定向原理,利用實際影像檢測POS數據中造成模型上下視差的主要誤差源。通過對試驗結果進行統計分析,建立系統誤差回歸補償模型,在無需區域網平差的情況下,直接通過相對定向消除POS系統誤差,使得模型上下視差明顯減小,定位精度有較大提高。

2 POS系統誤差存在的原因及其分析

根據POS的機理及特點,其系統誤差主要由以下幾個原因造成:

(1)視準軸誤差[9]:POS與航攝儀連接時,需要將IMU固聯在航攝儀上,由于安裝工藝上的原因,IMU與航攝儀的軸系不可能完全平行,一般來說,兩坐標軸系之間總存在著一個小的角度偏差(小于3°);

(2)累積漂移誤差[9]:在飛行過程中,由于運動加速度的存在,會形成作用在POS上的慣性干擾力矩,使POS獲取數據時產生進動(即漂移),從而引起測量誤差,即漂移誤差,通常IMU漂移誤差對目標定位精度的影響比 GPS漂移誤差更大;

(3)GPS失鎖和周跳:高精度 GPS衛星導航定位一般是用載波相位測量實現的。而載波相位測量只能測量相位中不足一整周的小數部分,整周部分的連續變化值由多普勒計數得到,飛機側傾轉彎、信號遮擋、信噪比低以及接收機故障等都會引起整周計數突變,稱為失周或失鎖,也稱為周跳。

(4)由像片畸變、地球曲率、大氣折光差等引起的誤差。

3 基于POS的立體像對相對定向

基于POS的立體像對相對定向以經典攝影測量理論為基礎[10],將傳統連續像對相對定向與單獨像對相對定向相結合,以POS提供的外方位元素作為初值,以左影像的角運動、右影像的直線運動和角運動實現相對定向,其通用誤差方程如式(1)所示。由于每個立體像對最多具有5個獨立的相對定向元素,因此一般在(φ1,κ1,BY,BZ, φ2,ω2,κ2)中選擇5個元素作為定向元素。本文為檢測POS數據中造成模型上下視差的主要誤差源,采用固定元素法,即在基于POS的立體像對相對定向的通用模型中固定某些相對定向元素,使其不參與平差迭代,只對其他定向元素進行迭代改正。因此固定φ1、κ1,對 BY、BZ、φ2、ω2、κ2進行迭代求解即為基于POS的連續法相對定向;固定BY、BZ,對φ1、κ1、φ2、ω2、κ2進行迭代求解即為基于POS的單獨像對相對定向。根據式(1)對相對定向元素進行迭代求解,當改正數小于給定限值時結束迭代。

4 POS系統誤差模型的建立及回歸分析

文獻[11]的研究表明,POS在定位測姿時會產生隨航攝飛行時間t呈線性關系的系統誤差。在建立誤差補償模型時,假設POS系統誤差y與飛行時間t之間的關系為線性關系,即

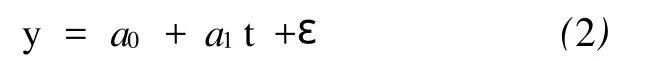
式(2)代表 y與t的線性回歸模型,a0、a1為未知的回歸參數;ε為隨機誤差項。假定t是一個非隨機變量,且沒有測量誤差,通過最小二乘法尋找最優估計量,使得隨機誤差項ε的平方和達到最小,從而獲得回歸參數a0、a1。

為檢驗以上線性回歸模型是否真實,應從兩個方面進行檢驗:①線性關系檢驗,即檢驗自變量和因變量之間的關系能否用一個線性模型表示;②回歸參數檢驗,即當線性關系檢驗通過以后,進一步檢驗每一個自變量對因變量的影響程度是否顯著。

相關系數 R2、檢驗統計量 F0、F0對應的概率P分別是用于檢驗回歸模型正確性的指標和檢驗參數,其中相關系數R2按下式得到

k為未知數個數;F0是服從 F(1,n-m-1)統計檢驗量,用于檢驗得到回歸變量t對y的影響是否顯著。通常 F0越大,變量 t越顯著,回歸模型的正確性越高。

5 試驗結果與分析

5.1 試驗影像概述

為了驗證本文所述算法的可行性,利用三組實際航空攝影影像數據進行試驗,試驗影像的資料參數如表1所示。三組試驗數據都利用數字攝影測量處理平臺DPGrid進行了自動轉點與量測,并人工立體量測了全部地面控制點的像平面坐標。

表1 三個試驗區航空攝影數據參數描述Tab.1 Image data description of three test areas

5.2 POS數據引起立體模型上下視差的主要誤差源檢測

在檢測POS數據恢復立體模型存在上下視差的主要誤差源時,首先需要確定主要誤差來源于線元素還是角元素。利用POS提供的外方位元素計算立體模型的上下視差;并根據基于POS的單獨像對相對定向,改正φ1、κ1、φ2、ω2、κ2五個角元素,計算相對定向后模型的上下視差;之后采用基于POS的連續法相對定向,左片外方位元素初值采用單獨像對相對定向改正后的值,右片仍以POS作為初值,以保證在計算模型上下視差時具有可比性。三種方法恢復立體模型后,統計三組試驗數據中每個模型的上下視差中誤差,并按航帶統計上下視差中誤差的最大值、最小值及平均值,統計結果如表2所示。

表2 三種不同方法計算立體模型的上下視差結果對比Tab.2 Comparison among vertical parallaxes of stereo models reconstructed with different methods

從表2的數據可以看出,利用POS提供的外方位元素計算立體模型的上下視差時,試驗1中5條航帶的上下視差中誤差平均值約為22個像素;試驗2中9條航帶的上下視差中誤差平均值約1個像素;試驗3中4條航帶的上下視差中誤差平均值在2個像素以內。經過單獨像對相對定向后,試驗1中5條航帶的上下視差中誤差平均值約為0.3個像素;試驗2中9條航帶的上下視差中誤差平均值也為0.3個像素左右;試驗3中4條航帶的上下視差在0.2個像素以內。而經過連續法相對定向后,模型上下視差與單獨像對相對定向試驗基本一致。由于兩種相對定向方法左片外方位元素一致,單獨像對相定向對右片的線元素與角元素均進行改正,而連續法相對定向只對右片角元素進行改正。該試驗結果說明POS數據中線元素對模型的上下視差影響很小,其主要誤差源在角元素中。

上述試驗已經確定POS中造成模型上下視差的主要誤差源來自角元素,根據基于POS的連續法相對定向原理,在固定左片方位元素的基礎上,分別固定右片的三個角元素、固定φ、固定ω、固定κ,求解其余相對定向元素,計算對應的模型上下視差并與基于POS連續法相對定向結果計算的模型上下視差進行比較,統計結果如圖1所示。

圖1 三組試驗數據上下視差統計結果對比Fig.1 Comparison among vertical parallaxes of three data sets

圖1的三組試驗數據當固定模型右片三個角元素時,在迭代過程中只是對線元素進行改正,而角元素的誤差不改正;在固定ω時,在迭代過程中對線元素及φ及κ角進行改正,ω角的誤差不改正。但從上圖可以看出,這兩種方式下計算出的模型上下視差非常接近。而固定φ與κ,其結果與步驟一中連續像對相對定向的上下視差非常接近。從而說明在POS數據中,角元素中包含的誤差主要集中于ω角,也就是說ω角是造成模型上下視差的主要誤差源。

5.3 POS數據系統誤差補償模型

將三組試驗測區相對定向后的POS數據與原始POS數據進行對比,計算出POS觀測值的三個外方位角元素(φ、ω、κ)的誤差。對三組試驗的POS觀測值中三個外方位角元素誤差與時間t進行線性回歸分析,得到如圖2的統計結果。可以看出φ和κ角的系統誤差未呈現出線性關系,而ω的系統誤差線性關系比較明顯。

圖2 POS角元素觀測值誤差對時間t的回歸分析Fig.2 Regression analysis between observation errorofangelelementof POS data and flying time

通過POS觀測值中φ、ω、κ誤差回歸分析結果對整個測區建立誤差補償模型,如表3所示。按照表3中回歸模型分別對三個角元素進行改正,用改正后的POS數據計算模型上下視差,將所得對應結果分別與相對定向后、原始POS數據求得的上下視差結果進行比較,如圖3所示。

表3 POS觀測值中φ、ω、κ誤差回歸分析結果表Tab.3 Regression analysis of observation error ofφ,ω andκ

圖3 各角元素補償改正后求得的模型上下視差比較圖Fig.3 Comparison among vertical parallaxes of POS data corrected by angle regression model

從上述圖表結果可以看出,φ和κ角與時間t無明顯回歸關系,各時間t的誤差點離散地分布在回歸直線附近,且利用相應回歸模型改正后,模型上下視差無明顯減小。而ω角誤差與時間t成明顯線性回歸關系,其相關系數 R2非常接近于1,檢驗統計量 F0也很大,利用該回歸模型改正后,模型上下視差明顯減小。

將三組試驗區的控制點作為檢查點,分別利用原始 POS數據、ω角誤差補償模型改正后的POS數據進行前方交會,表4列出了所有控制點在消除平移誤差后前方交會結果與外業測量坐標的較差。可以看出,改正后的POS數據前方交會獲得的檢查點平面精度和高程精度分別提高了0.5～1.0倍和1.0～2.0倍,完全滿足1∶10 000比例尺正射影像制作的要求。

表4 原始POS數據和改正后的POS數據前方交會結果Tab.4 Comparison between results of forw ard intersection with original and rectified POS data m

6 結 論

本文對POS數據引起模型上下視差的主要誤差源進行了檢測,成功建立了誤差補償模型,并證明了該模型的正確性與可行性。利用1∶78 000、1∶72 000和1∶83 000三種攝影比例尺的航空攝影影像進行試驗的結果表明:

(1)POS系統提供的影像外方位元素中,線元素誤差對模型的上下視差影響較小,ω角誤差是造成模型上下視差的主要誤差源。

(2)建立了角元素的誤差補償模型,通過回歸分析及控制點前方交會試驗證明ω角誤差補償模型可以很好地對ω角進行改正,消除其系統誤差。

(3)POS數據ω角系統誤差改正后,無需區域網平差即可滿足1∶10 000比例尺正射影像制作的精度要求;但由于其他元素的誤差沒有改正,因此改正結果不能完全滿足1∶10 000比例尺立體測圖精度的要求。作者進行過試驗驗證,基于上述三組數據進行POS輔助的無控制點區域網平差后獲得的方位元素均可完全滿足立體測圖精度要求。

正是由于POS系統提供的像片外方位元素在用于實際航測地形測圖生產時會產生作業員無法忍受的模型上下視差,因此POS數據只能用于制作數字正射影像圖,而無法用于地形測圖。本文研究一種行之有效的模型上下視差消除方法,提高了POS數據的定位精度,對于充分發揮POS系統的作用并更好地服務于困難地區的基礎地理信息獲取有一定意義。

[1] ACKERMANN F.Practical Experience with GPS-supported Aerial Triangulation[J].Photogrammetric Record,1994, 16(84):861-874.

[2] YUAN Xiuxiao.POS-supported Bundle Block Adjustment [J].Acta Geodaetica et Cartographica Sinica,2008 37(3): 342-348.(袁修孝.POS輔助光束法區域網平差[J].測繪學報,2008,37(3):342-348.)

[3] YUAN Xiuxiao,LI Deren.Some Investigation for GPS-supported Aerotriangulation [J]. Acta Geodaetica et Cartographica Sinica,1997,26(1):14-19.(袁修孝,李德仁.GPS輔助空中三角測量的若干探討[J].測繪學報, 1997,26(1):14-19.)

[4] YUAN Xiuxiao.Analysis of Y-parallax of Stereo Model Reconstructed Using Elements ofExteriorOrientation Determined by Position and Orientation System [J]. Geomatics and Information Science of Wuhan University, 2007,32(10):856-859.(袁修孝.POS數據用于立體模型恢復時的上下視差分析[J].武漢大學學報:信息科學版,2007,32(10):856-859.)

[5] GREENING T,SCHICKLER W,THORPE A.The Proper Use of Directly Observed Orientation Data:Aerial Triangulation is Not Obsolete[C]∥Proceedings of 2000 ASPRS Annual Conference.Washington DC:ASPRS,2000.

[6] GRUEN A,BAER S.Aerial Mobile Mapping—Georeferencing without GPS/INS[C]∥Proceedings of the 3rd International Symposium on Mobile Mapping Technology. Cairo:[s.n.],2001.

[7] JACOBSEN K,WEGMANN H.Dependencies and Problems of Direct Sensor Orientation[C]∥Proceedings of the OEEPE Workshop on Integrated SensorOrientation. Hannover:[s.n.],2001.

[8] CRAMER M,STALLMAN D.System Calibration for Direct Georeferencing[J].International Archives of Photogrammetry and Remote Sensing,2002,34:79-84.

[9] HONKAVAARA E.Calibration Field Structures for GPS/ IMU/Camera-system Calibration[J].The Photogrammetric Journal of Finland,2003,18(2):3-15.

[10] WAN G Zhizhuo.Principles of Photogrammetry[M]. Beijing:Surveying and Mapping Press,1990.(王之卓.攝影測量原理[M].北京:測繪出版社,1990.)

[11] ACKERMANN F.GPS for Photogrammetry[C]∥Proceedings of Tutorial on Mathematical Aspects of Data Analysis.[S.l.]:ISPRS.1991:17-70.