超高階次勒讓德函數遞推計算中的壓縮因子和Horner求和技術
劉纘武,劉世晗,黃 歐
1.信息工程大學理學院,河南鄭州450001;2.鄭州市市政工程總公司,河南鄭州450007;3.美國俄亥俄州立大學地球科學學院,俄亥俄哥倫布43210
1 引 言
由于當今衛星跟蹤技術、衛星測高以及重力場求解技術的發展,國內外正在把高階次重力場模型向更高階次擴展[1-5]。顯然,超高階次球諧位系數模型的構制與應用,與超高階次締合勒讓德函數及其導數的計算密切相關。并且,隨著航天技術的不斷發展,需要構建的位系數模型的階次越來越高。因此,研究計算超高階次締合勒讓德函數及其導數值的方法是非常必要的[4,6-7]。
由締合勒讓德函數及其關于θ的導數構成的球諧級數表達式為
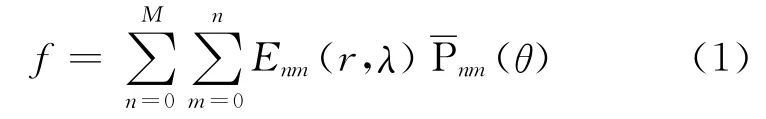
和
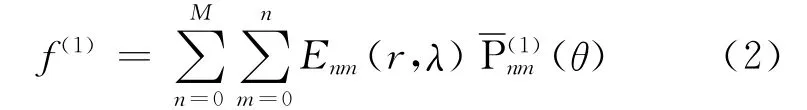
式中,(r,θ,λ)是空間點的球面坐標,r是點至地心的距離,θ是地心余維,λ是經度;M是球諧展開式的最大階數;Enm(r,λ)是與階n和次m有關的(r,λ)的函數;和是n階m次第一類完全正常化締合勒讓德函數和它們的導數。
例如,在點(r,θ,λ)處,地球外部擾動位T(r,θ,λ)的M階球諧級數表達式為[8]
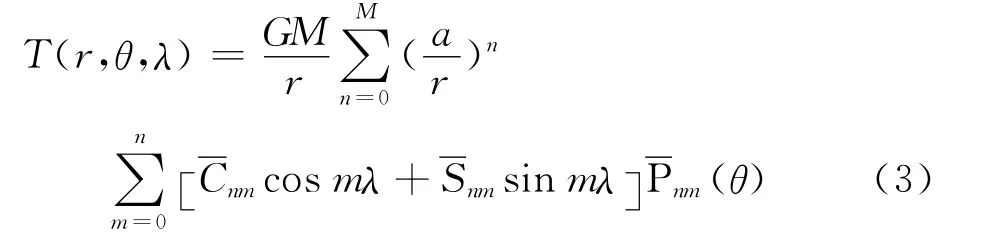

這里
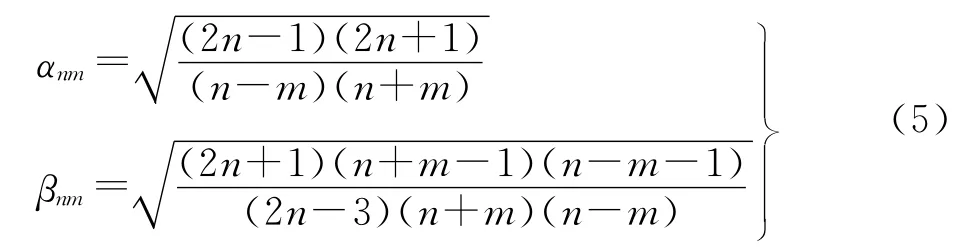
式中,
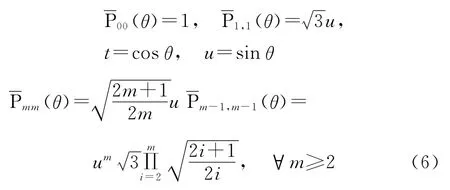
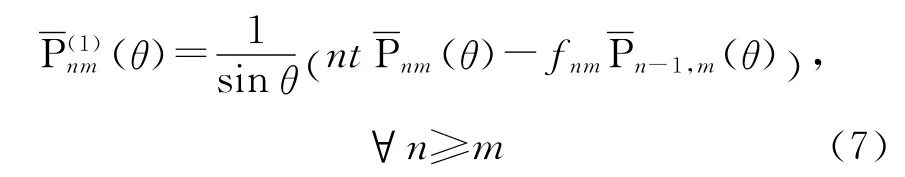
式中
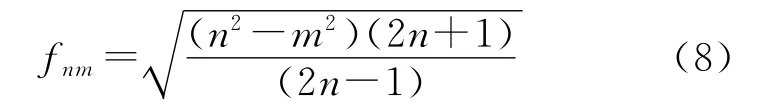
按式(4)~式(8)遞推計算,當M=2 500在接近兩極時函數值達到10-4000量級[4,6]。而一般個人計算機的允許數值范圍約在10-310和10+310之間[10]。為了避免下溢,文獻[4]修改遞推式(4)和式(7)為

計算式(1)采用如下Horner求和技術[4,12]

式中,
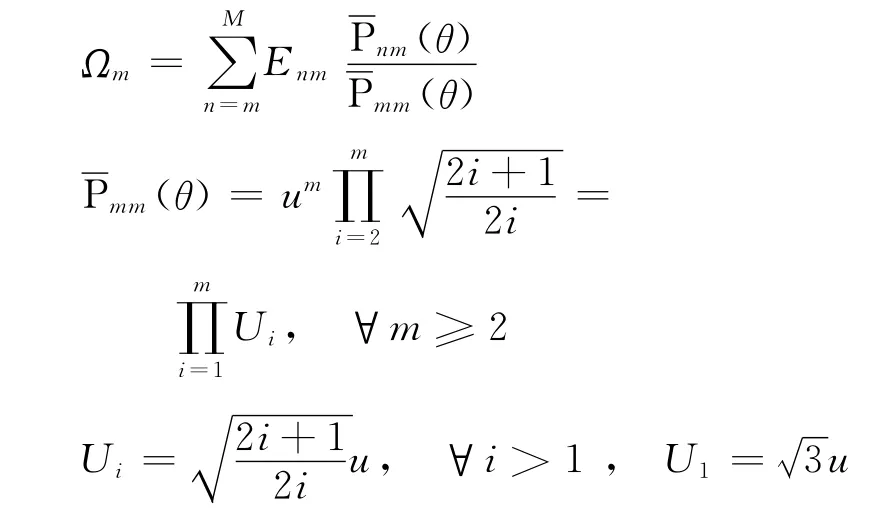
式(2)可以類似計算。
的值當M=2 700,θ→0°時將超過10500。為了避免上溢,遞推過程中乘以一個下調因子[4]10-280。
2 遞推計算中的壓縮因子和復合Horner求和技術
分析式(9)中的系數因子t、αnm和βnm不難發現,對確定的θ和m,當n很大時,βnm接近于1;當θ→0°時t→1,且它不隨m和n的變化而變化;而隨著n的增大αnm趨于2(對于固定的m),且當m<n<1.666 7 m時αnm>2.5。因此,每一列遞推,n由m增大到n=1.666 7 m,每一步遞推值將增大超過αnm/βnm=1.5倍。例如,當n由m= 2 700增大到n=1.666 7 m(約4 500)時,如果不顧及t的微小影響,遞推值將遠遠超過初始值的9×10316(實際超過1×10500)倍以上。
鑒于以上分析,在遞推中插入壓縮因子q,式(9)變為
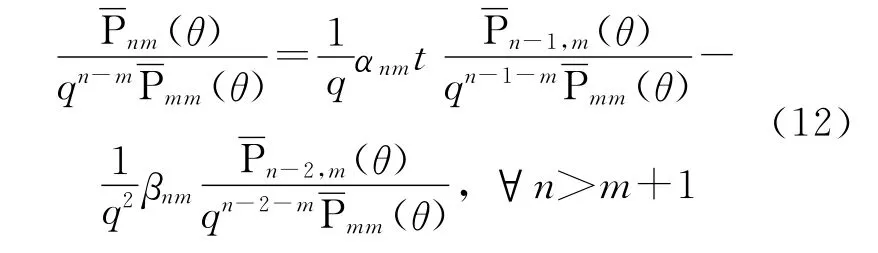
式中,q是與θ有關的介于1和2之間的一個數。顯然,與式(9)相比,式(12)降低了遞推值增大的速度。
當θ逐漸增大到90°時,t=cosθ逐漸減小到0,式(9)右端第一項作用越來越小,遞推值主要依賴于第二項。為避免下溢,這時取q=1。由此,定義q為

式中,ρ是一個介于0.5和1之間的常數;k是一個正整數。令
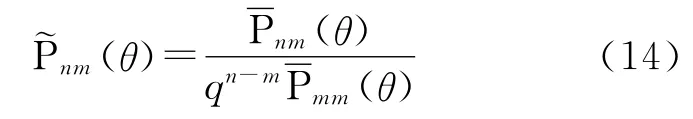
式(12)改寫為
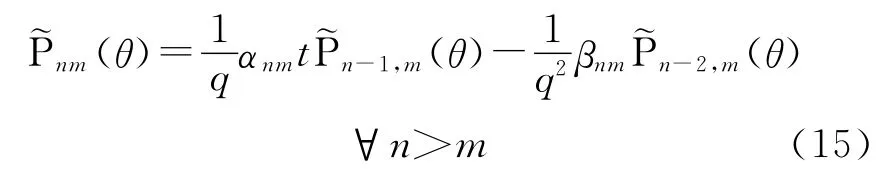

式中,
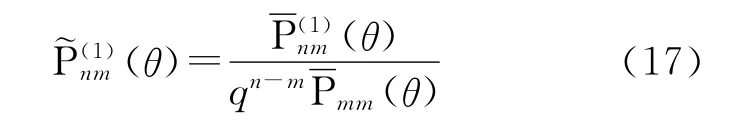
式(1)的值如下計算
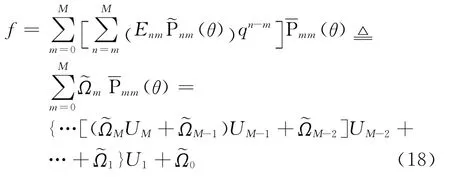
式中,
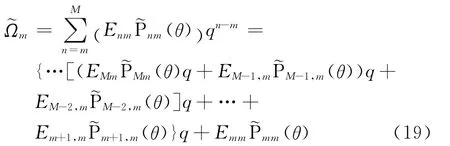
式(18)和式(19)合稱為復合Horner求和技術。
式(2)中f(1)可以類似計算。
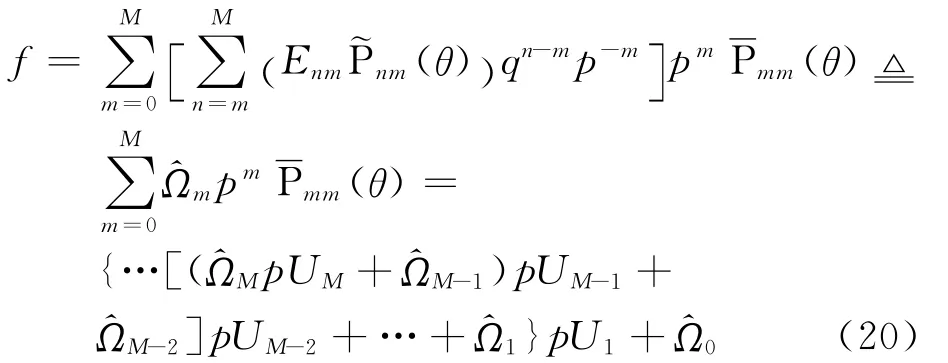
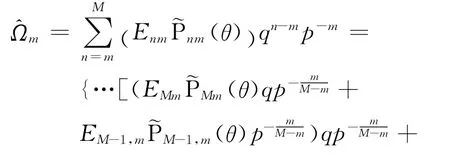
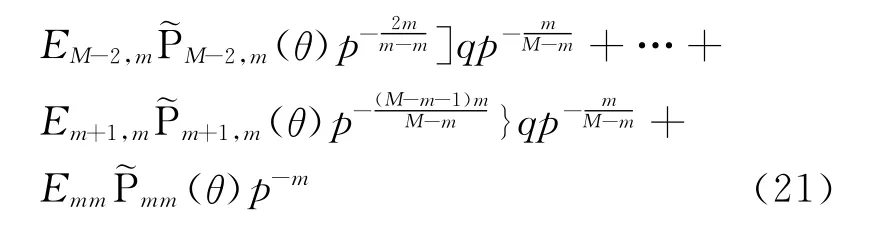
式(20)和式(21)也可合稱為復合Horner求和技術。
3 數值檢驗
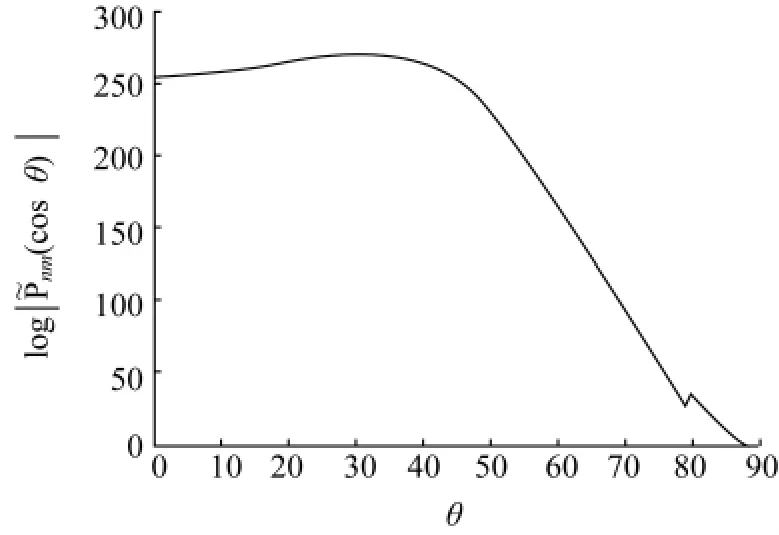
圖1 |(θ)|(?n,m≤3 600)的最大值的對數值曲線Fig.1 Logarithm plot of maximum values of|(θ)|(?n,m≤3 600)

圖2 |(θ)|(?n,m≤3 600)的最小值的對數值曲線Fig.2 Logarithm plot of minimum values of|(θ)|(?n,m≤3 600)
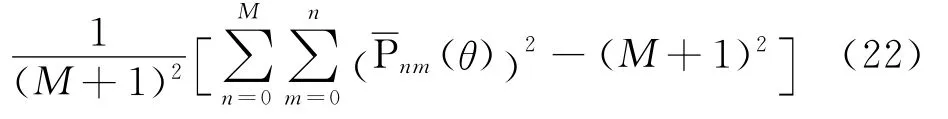
式中,

式(23)、式(24)類似于式(20)、式(21)計算。
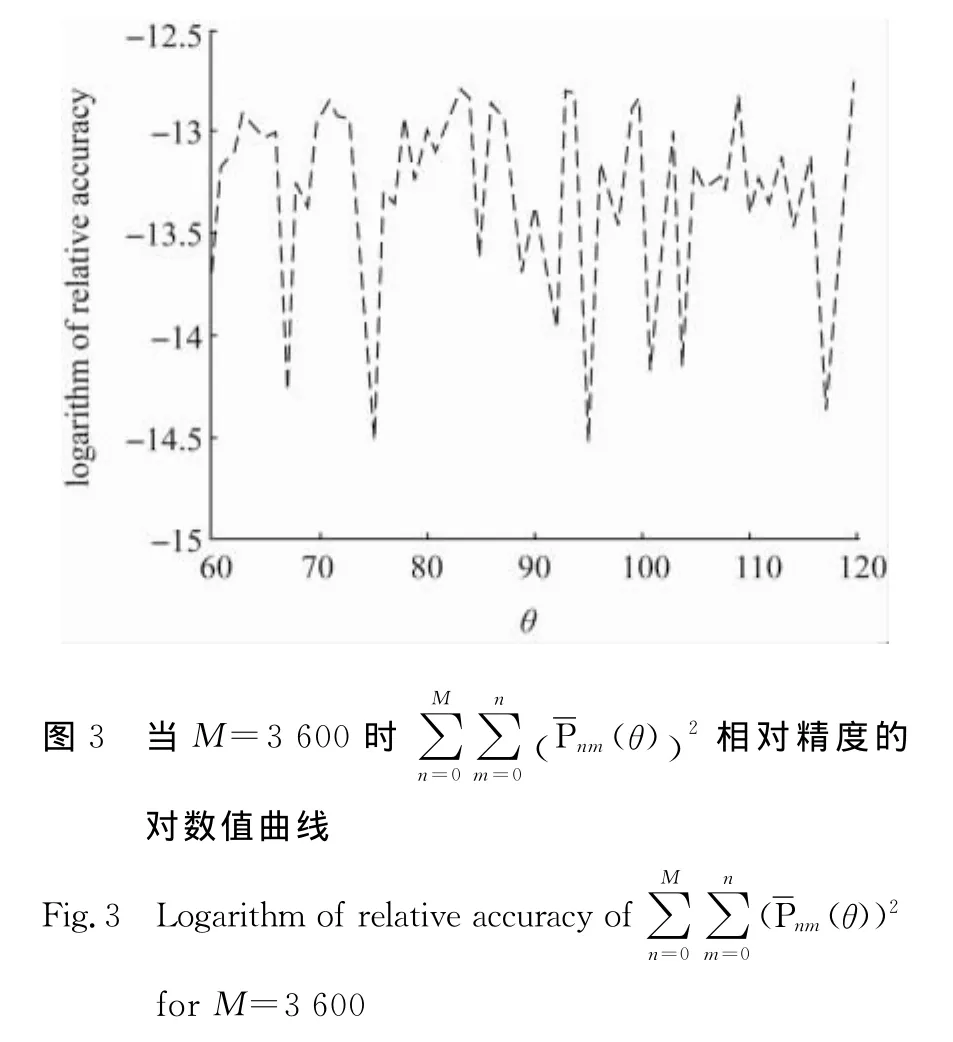
從圖3看到,新算法求得的完全正則化締合勒讓德函數值具有較高的精度,同時圖1~圖3也說明新算法有較好的穩定性。
Belikov遞推法的計算公式為
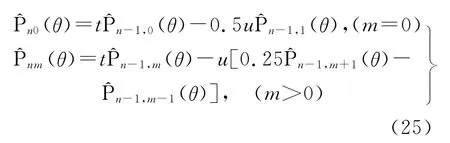
式中,

跨階次遞推法的計算公式為
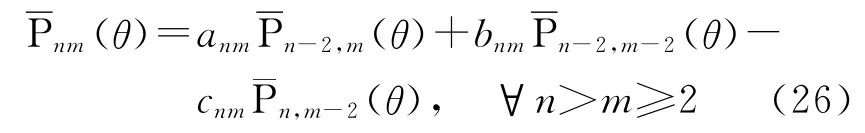
式中,

由于式(25)和式(26)的遞推系數都小于1,因此比式(4)的穩定性要強。但在接近兩極時的值仍然達到10-4000量級,超出一般計算機的允許數值范圍而下溢。根據式(25)和式(26)的結構,不能像式(9)那樣處理。不過,式(25)可改寫為
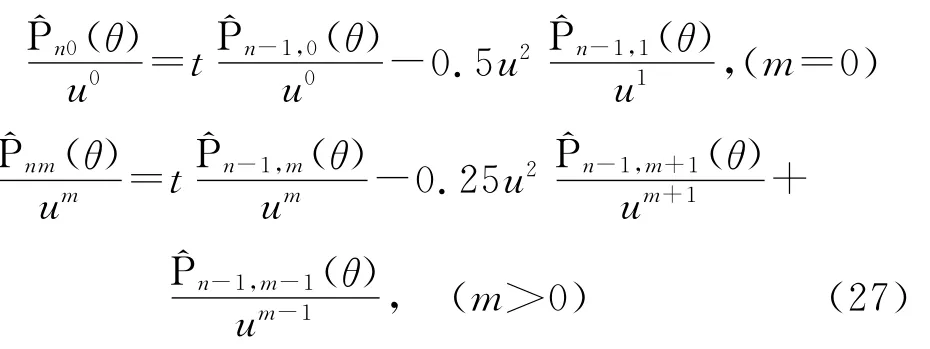
由式(27)計算^Pnm(θ)/um可避免下溢,且若遞推中乘以10-280,可計算至2 500階不會上溢。由此轉化為就可類似式(11)計算式(1)。但當M>2 500時出現上溢,若要進一步提高計算的階次,因^Pnm(θ)/um由三項構成,則壓縮因子結構非常復雜。
跨階次遞推式(26)若如法處理,則產生系數βnm/u2和γnm/u2,當θ→0°它們急劇變大,雖然避免了下溢,但很快出現上溢。由此分析,利用本文的處理思想,當階次很高時,無法避免遞推值的溢出。
4 結 論
在個人計算機上執行現有的遞推公式計算超過M>2 700階次的締合勒讓德函數會產生上溢或下溢。通過在基本遞推算法中插入壓縮因子法,避免了溢出現象的發生。同時給出了計算由完全正則化締合勒讓德函數構成的超高階球諧級數式的復合Horner求和技術。數值檢驗表明新算法具有較高的精度。
毫無疑問,在大地測量中會有包含真實擾動位系數在內的計算締合勒讓德函數級數f的更嚴密的檢測方法。本文重點在于提出締合勒讓德函數遞推的壓縮因子算法和復合Horner求和技術的思想。依據這個思路,Belikov遞推法可以類似處理,且遞推計算更高階的締合勒讓德函數級數及確定相應的級數求和技術,都會涉及更為復雜的壓縮因子和球諧級數求和手段;任意高階的締合勒讓德函數遞推算法及其相應的級數求和問題,必須要有新的思想和方法;跨階次遞推法很難利用本文給出的方法處理下溢問題。對以上問題,將進一步研究。
[1] WENZEL G.Ultra-high Degree Geopotential Models GPM98A,B,and C to Degree 1 800[C]∥Joint Meeting of the International Gravity Commission and International Geoid Commission.Trieste:[s.n.],1998.
[2] LIU Zuanwu,LU Zhonglian.A Study of Incomplete Geopotential Coefficient Model[J].Geophysics,1998,41(1):89-98.
[3] HUANG Motao,ZHAI Guojun,OUYANG Yongzhong,et al.Analysis and Computation of Ultra High Degree Geopotential Model[J].Acta Geotaetica et Cartographica Sinica,2001,30(3):208-213.(黃漠濤,翟國君,歐陽永忠,等.超高階地球位模型的計算與分析[J].測繪學報,2001,30(3):208-213.)
[4] HOLMES S A,FEATHERSTONE W E.A Unified Approach to the Clenshaw Summation and the Recursive Computation of Very High Degree and Order Normalised Associated Legendre Functions[J].Journal of Geodesy, 2002,76(5):279-299.
[5] PAVLIS N K,HOLMES S A,KENYON S C,et al.Earth Gravitational Model 2008(EGM2008)-WGS-84Version[EB/OL].[2010-02-20].http:∥earth-info.nga.mil/GandG/WGS-84/gravitymod/egm2008/index.html.
[6] JEKELI C,LEE J K,KWON J H.On the Computation and Approximation of Ultra-high Degree Spherical Harmonic Seies[J].Journal of Geodesy,2007,81(9):603-615.
[7] WANG Jianqiang,ZHAO Guoqiang,ZHU Guangbin.Contrastive Analysis of Common Computing Methods of Ultra-high Degree and Order Fully Normalized Associated Legendre Function[J].Journal of Geodesy and Geodynamics,2009,29(2):126-130.(王建強,趙國強,朱廣彬.常用超高階次締合勒讓德函數計算方法對比分析[J].大地測量與地球動力學,2009,29(2):126-130.)
[8] HEISKANEN W A,MOTITZ H.Physical Geodesy[M].San Francisco:Freeman,1967.
[9] COLOMBO C.Numerical Methods for Harmonic Analysis on the Sphere:Rep 310[R].Columbus:Ohio State University,1981.
[10] OVERTON M L.Numerical Computing with IEEE Floating Point Arithmetic[M].Philadelphia:SIAM,2001.
[11] KOOP R,SPTELPSTRA D.On the Computation of the Gravitational and Its First and Second Order Derivatives[J].Manuscripta Geodaetica,1989(14):373-382.
[12] GLEASON D M.Partial Sums of Legendre Series via Clenshaw Summation[J].Manuscr Geod,1985(10):115-130.

