混合氣體瀉流分子束中兩種分子的相對速率分布

宮衍香，胡承忠，李 峰，吳曉梅

(1.泰山學院物理與電子工程學院，山東泰安 271021;2.南京大學天文與空間科學學院，江蘇南京 210097)

瀉流現象在分子速率分布的測定，同位素分離等方面有許多應用.例如，驗證氣體分子的速率分布是否與麥克斯韋分布律的理論預測相符的葛正權實驗以及密勒和庫什實驗，都利用了由瀉流形成分子束的技術.在分離同位素方面，使用常溫時為氣態的UF6，可以借助于瀉流現象把較輕的235UF6和較重的238UF6分離，從而就能獲得具有較高濃度的235U核燃料［1］.平衡態下或瀉流過程中分子的速率分布是統計物理學中的一個重要課題.很多文章或教材對這類問題做過詳細的討論［2－10］.其中涉及一種組分的速率分布、混合氣體的相對速率分布、瀉流分布函數、相對論條件下的麥克斯韋分布以及利用分布函數求擴散方程、擴散系數和內摩擦系數等問題.但對于混合氣體的瀉流問題少有討論，而氣體混合是更為普遍的情形.例如上述同位素的分離可視為與混合氣體瀉流有關的現象.本文討論了混合氣體瀉流分子束中兩種組分的相對速率分布、相對速率的平均值和方均根速率等問題.如果系統為單一成分，分子的平均碰撞頻率和自由程的計算較為簡單.當氣體為混合氣體時，計算分子的平均碰撞頻率時則要記及分子數密度、碰撞截面(與兩種分子的有效直徑有關)和平均相對速率所造成的變化.其中，平均相對速率要用相對分布函數來計算.本文討論了混合氣體的瀉流現象，導出了相對平均速率，這對于研究瀉流分子束中兩種分子的平均碰撞頻率和平均自由程有幫助，具體的影響將在討論部分給予說明.和經典麥克斯韋速率分布函數的推導一樣，本文仍然考慮近獨立粒子系統，即不考慮分子間的相互作用.

1 瀉流氣體中分子的相對速率分布

如圖1所示，圓圈和黑點表示2種氣體分子，坐標為笛卡爾坐標，y軸垂直于紙面向里，z軸為小孔面元垂直于氣壁向外的法線方向.θ為對應球坐標系中的方位角.設容器中理想氣體溫度為T，某種分子的質量為m、單位體積的分子數為n.瀉流分子的速度分布函數為:

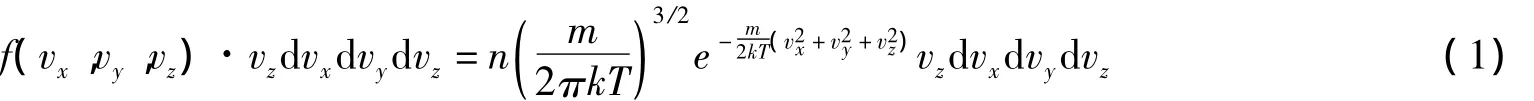
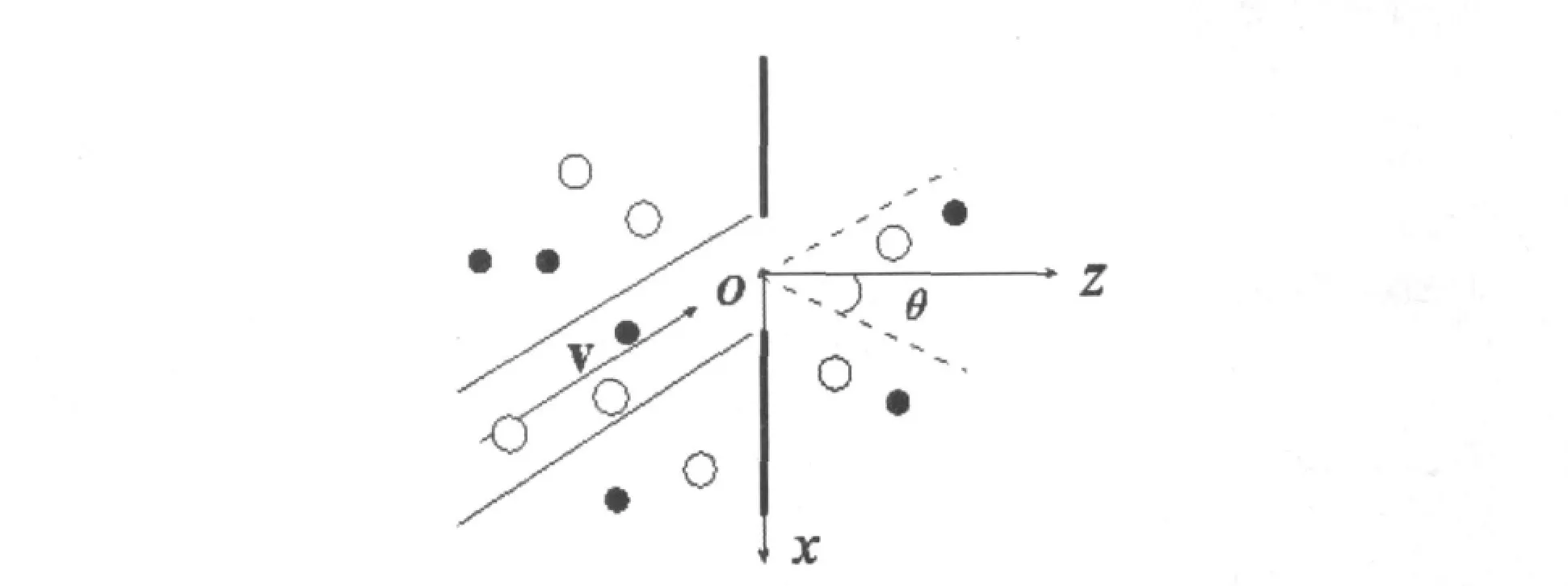
圖1 混合氣體的小孔瀉流示意圖

其中f(vx，vy，vz)為麥克斯違速度分布函數，(1)式的物理意義為:單位時間，通過小孔的單位面積瀉流出的、速度介于vx～vx+d vx，vy～vy+d vy，vz～vz+d vz之間的分子數.首先把它歸一化，即對(1)式積分，注意vz的積分范圍為0～+∞，有

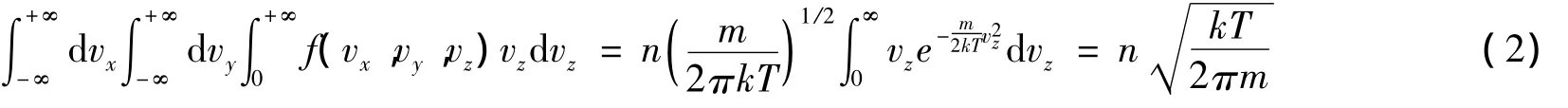
則歸一化的分布函數為

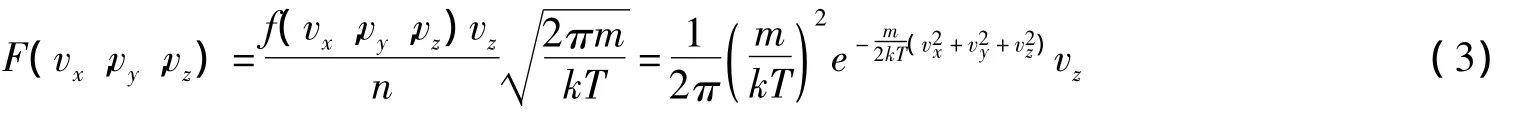
這和麥克斯韋速度分布函數的不同在于乘積中的vz，后面會看出，正是這個因子使的混合氣體的瀉流分布函數出現了新的特點.把(1)式變換到速率的球極坐標空間可得瀉流速率分布函數，見文獻［5］.

設混合氣體由兩種分子構成，分別標記為“1”和“2”，可以認為兩種氣體分子的速度分布是相互獨立而互不關聯的，根據幾率相乘的性質可知，兩種氣體分子同時各自處于相應的速度間隔d v1xd v1yd v1z和d v2xd v2yd v2z的幾率為:

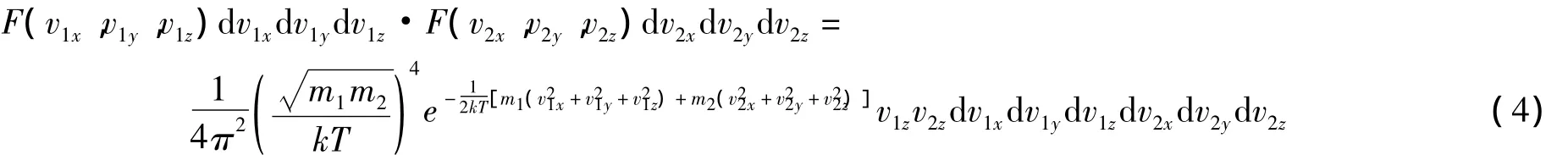
設兩種分子的相對速度為ˉvr，質心速度為ˉvc，即有

這里需要強調一下，考慮到分子速度的大小和方向有各種可能性，從定義式(5)可以看出，ˉvr的范圍仍可以取－∞ ～+∞，方向任意，所以ˉvr的3個分量vrx，vry，vrz的取值范圍均為－∞ ～+∞.而對于ˉvc，因為分子速度的z分量只有大于0才可能發生瀉流，所以vcz的范圍應取0～+∞，vcx、vcy的取值范圍仍為－∞～+∞.由(5)式可得

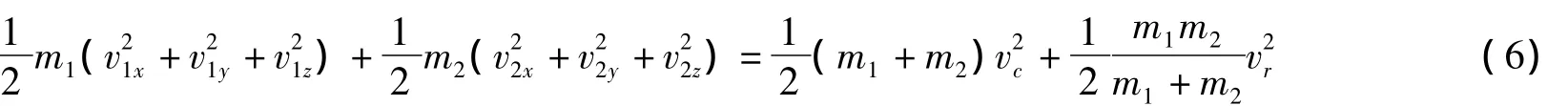
可將積分變量ˉv1、ˉv2轉換成ˉvr、ˉvc，根據變量轉換的雅可比關系，有

由(5)式可得

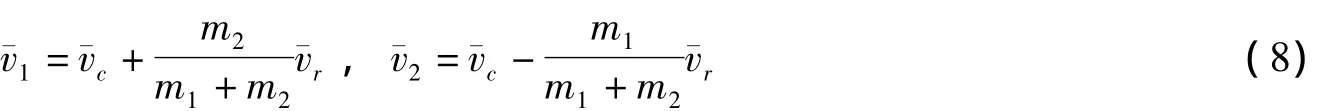
則雅可比行列式為

把速度間隔轉換到速度的球極坐標空間，則有

由(8)式可知

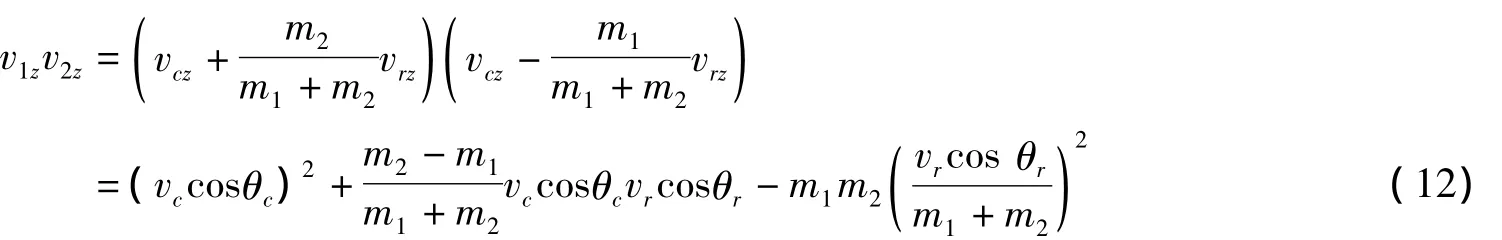
把(6)式和(9)－(12)式代入(4)式，幾率變為

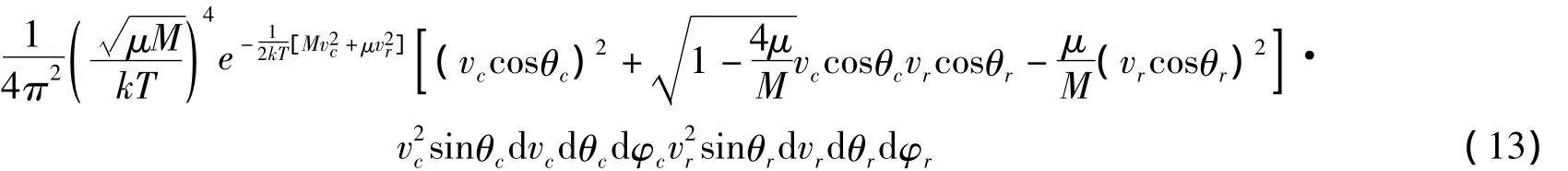
其中，M=m1+m2為總質量，μ=m1+m2/(m1+m2)為折合質量.與容器內混合氣體的相對速率分布不同，分布函數(13)無法寫成關于M和μ對稱的形式了(見文獻［9］).保留變量vr，把(13)式的其他變量積分，由前面對各速度分量的分析可知，各新變量的取值范圍:φr和φc由0～2π，θr由0～π，vc由0～∞，而θc須由0～π/2.則有

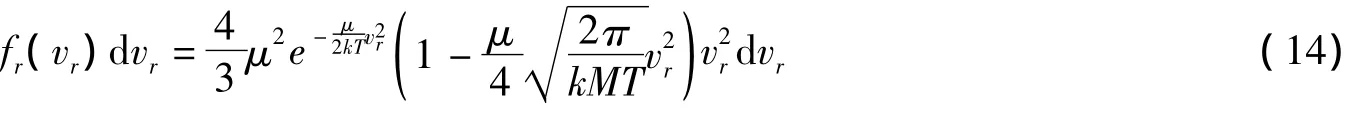
把它歸一化，則為

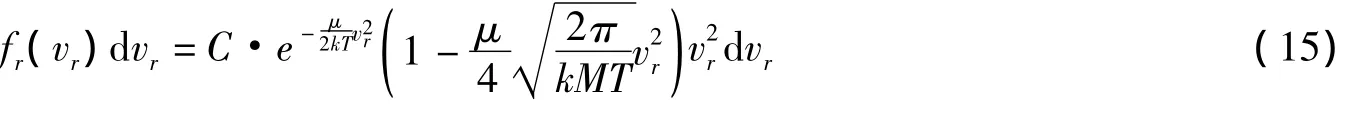
其中歸一化系數為

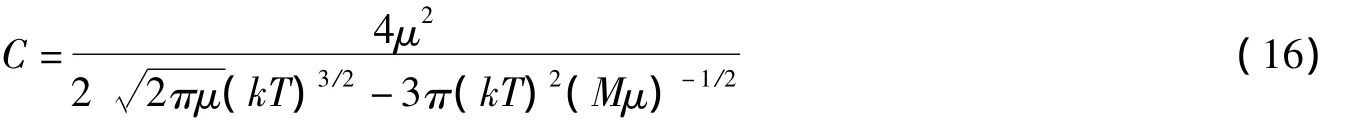
(15)式即瀉流氣體中兩種分子的相對速率分布.表1對四種分布函數進行了對比，通過比較可以發現，這種分布函數與一般的麥克斯韋分布函數的最大不同在于括號中的第二項，這一項是因為公式(3)中vz的出現造成的，而其它三種分布函數的形式皆為c1exp(－c2v2)vn，其中，c1，c2和n為相應的系數.但有意思的是，分布函數形式上的這種差別，并未改變分布函數曲線的形態(見圖3).

2 各種分布函數的比較

由(15)式，可求出瀉流分子相對速率的平均值

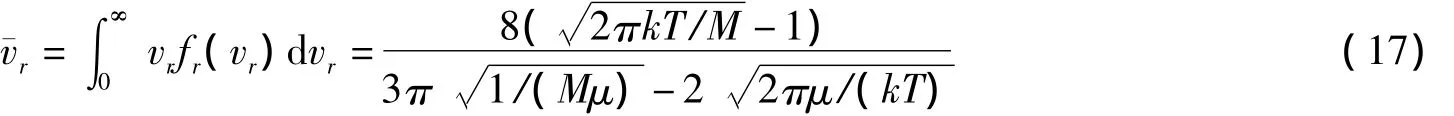
如果只有一種分子，則M=2m，μ=m/2，瀉流氣體相對速率的平均值為

相對方均根速率vrs是v2r的平均值的平方根:

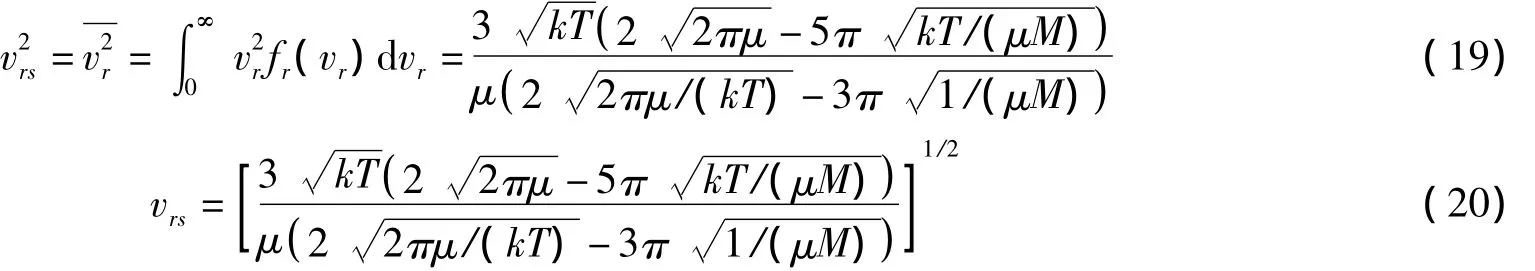
只有一種分子，相對方均根速率為

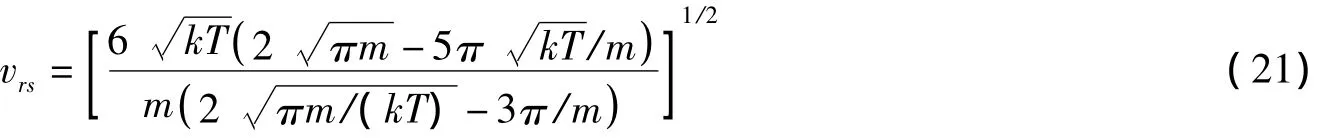
各種情況下的分布函數、平均(相對)速率、方均根(相對)速率對比，見表1.

表1 對混合氣體分布函數，取m1=m2=m時的速率值

為了直觀的比較四個分布函數，本文以氧分子為例采用Maple軟件繪圖.所采用數據m=5.32× 10－26kg，T=300K，k=1.38×10－23J·K－1.對于混合氣體取M=2m，μ=m/2.圖2中曲線按照粗細依次為f1，f2，f3，與表1中的前三個分布函數順序一致.相比較而言，由于混合瀉流分子相對速率分布的函數值非常小，如果把其與前三個函數畫在同一坐標系中將近乎一條沿x軸的線段，故將其單獨繪制在一張圖中，即圖3.

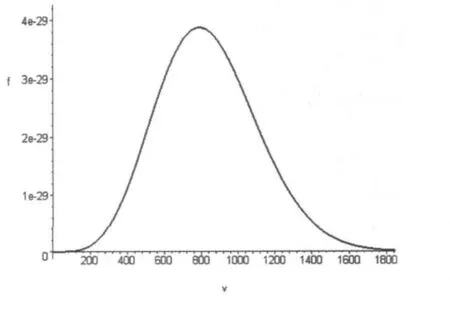
圖3 混合瀉流分子相對速率分布函數

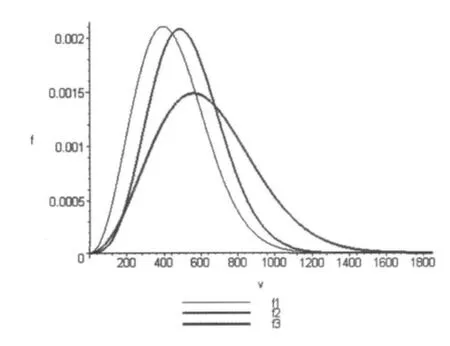
圖2 前三種分布函數圖

3 討論

瀉流現象在分子速率分布的測定，同位素分離等方面有許多應用.本文討論了混合氣體的瀉流現象，導出了瀉流分子的相對速率分布，求出了相對平均速率，這對于研究瀉流分子束中兩種分子的平均碰撞頻率和平均自由程有幫助.比如一個分子“1”與分子“2”的平均碰撞頻率為Z12=vˉrn2σ12=πd212n2vˉr，其中d12=(d1+d2)/2為兩種分子的平均直徑，σ12為“1”，“2”分子間的碰撞截面，n2應理解為瀉流氣體中單位體積內分子“2”的平均分子數(或根據適當的條件估算).在混合瀉流氣體中，分子“1”的平均碰撞頻率Zˉr等于分子“1”與其他“1”分子間的平均碰撞頻率Zˉ11以及分子“1”與分子“2”的平均碰撞頻率Zˉ12之和，對于“2”分子用類似的方法可以得到其平均碰撞頻率.瀉流分子的相對速率分布函數的函數圖形與一般的分布函數圖形相似.限于實驗條件的限制，我們并不期望通過實驗方法來檢驗該分布函數.但從圖3可以看出，分布函數曲線符合一般分布函數的特點(高斯分布)，這可以間接的證明理論方法的正確性.

［1］瑞夫F.統計物理學［M］.周世勛，徐正惠，龔少明，譯.北京:科學出版社，1979.

［2］陸興中，吳祥明.由麥克斯韋速率分布和自由程分布導出內摩擦系數［J］.大學物理，2004，23(2):13－14.

［3］唐瑩，佘守憲.麥克斯韋分子速率分布律與擴散方程、擴散系數的初淺推導［J］.大學物理，2001，20(11):16－19.

［4］吳瑞賢，吳世英.速度分布、速率分布中的幾率最大問題［J］.大學物理，1988，22(7):44－45.

［5］黃瑞.關于麥克斯韋速率分布律的幾點分析［J］.大學物理，1988，13(12):32－34.

［6］程復興.瀉流速率分布函數及其應用舉例［J］.大學物理，1984，12(5):32－33.

［7］陳忠勝.相對論條件下的麥克斯韋分布［J］.大學物理，1989，(1):21－22.

［8］劉風芝，吳玉喜，韓立堯.瀉流中氣體性質變化的探討［J］.大學物理，2002，21(11):21－23.

［9］汪志誠.熱力學統計物理(第三版)［M］.北京:高等教育出版社，2003.

［10］陳仁烈.統計物理學引論(增訂本)［M］.北京:人民教育出版社，1959.