基于PIFOWA算子的直覺模糊信息集結方法

陳志敏，梁 霞

(曲阜師范大學管理學院，山東日照 276826)

1 引言

多屬性決策的實質是在多個候選方案中，選擇一個最滿足一組評價指標的方案.在現實生活中，決策者往往不能提供對決策方案的精確偏好信息，而存在一定的猶豫度或表現出一定程度的知識的缺乏，Atanassov在1983年提出的模糊集［1－2］，可以更細膩的刻畫客觀事物的模糊性本質，利用它所增加的非隸屬度函數，可以同時表示出決策者支持和反對的程度，在處理模糊性和不確定性方面更具靈活性和實用性.因此，研究直覺模糊環境下的多屬性決策問題在理論和實際應用中都有重要意義.

關于直覺模糊信息的集結，徐澤水和Yager提出了直覺模糊加權幾何(IFWG)算子［3］和直覺模糊有序加權幾何(IFOWG)算子.2007年徐澤水又把OWA算子拓展到直覺模糊集上，提出了直覺模糊加權平均(IFWA)算子［4］，直覺模糊有序加權平均(IFOWA)算子［4］和直覺模糊混合平均(IFHA)算子［4］，并給出了基于這些直覺模糊信息集結算子的決策方法。利用直覺模糊集結算子進行信息集結時，屬性間是公平的，是完全可以補償的，而實際決策問題中常常存在屬性間不容易補償的情況.例如，航空公司在燃料的耗費和飛行安全之間做決定時，顯然不能用節省燃料的費用來彌補飛行的安全上的缺失，安全性的優先權大于燃料費用的優先權.針對這類屬性間不容易補償的情況，2004年Yager研究了屬性間具有優先級別關系的多屬性決策問題［5］，指出具有較低優先權的屬性的重要性應建立在方案對較高優先權的屬性的滿足程度的基礎上.2008年，Yager給出了四種屬性間具有優先級別關系的集結算子［6］，即PS (prioritized scoring)算子，PA(prioritized averaging)算子，PRI－AND算子，PRI－OR算子.2009年，Yager提出了POWA(prioritized ordered weighted averaging)算子［7］.本文針對屬性值為直覺模糊數的多屬性決策問題，在IFOWA算子的基礎上，將POWA算子拓展到直覺模糊集的情形，提出屬性間具有優先級別關系的直覺模糊有序加權平均(PIFOWA)算子，最后給出了實例分析.

2 直覺模糊集與IFOWA算子

定義1［1－2］設X是一個非空集合，則稱A={〈x，μA(x)，vA(x)〉|x∈X}為直覺模糊集，其中μA(x)和vA(x)分別為X中元素x屬于A的隸屬度和非隸屬度，即

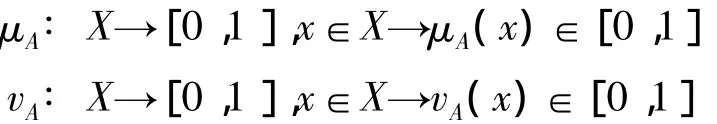
且滿足條件:0≤μA(x)+vA(x)≤1，x∈X.此外，πA(x)=1－μA(x)－vA(x)，x∈X表示X中元素x屬于A的猶豫度或不確定度.

定義2［3］稱α=(μα，vα)為直覺模糊數，其中μα∈［0，1］，vα∈［0，1］，μα+vα≤1.且設Θ為全體直覺模糊數的集合，顯然，α+=(1，0)為最大的直覺模糊數，α－=(0，1)為最小的直覺模糊數.

定義3［3］直覺模糊數的運算法則:

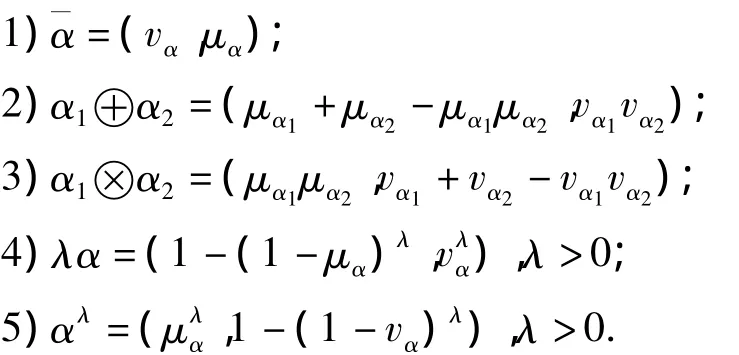
對任一直覺模糊數α=(μα，vα)，Chen和Tan［8］定義其得分函數s(α)=μα－vα，s(α)∈［－1，1］.Hong和Choi［9］定義其精確函數為h(α)=μα+vα，h(α)∈［0，1］.為了比較兩個直覺模糊數的大小，基于以上兩個函數，徐澤水［4］在2006年提出了比較兩個直覺模糊數大小的方法.

定義4［3］設α1=(μα1，vα1)，α2=(μα2，vα2)為直覺模糊數，s(α1)=μα1－vα1和s(α2)=μα2－vα2分別為α1和α2的得分值，h(α1)=μα1+vα1和h(α2)=μα2+vα2分別為α1和α2的精確度，則

若s(α1)＜s(α2)，則α1小于α2，記為α1＜α2;

若s(α1)=s(α2)，則

1)若h(α1)=h(α2)，則α1和α2相等，即μα1=μα2，vα1=vα2，記為α1=α2;

2)若h(α1)＜h(α2)，則α1小于α2，記為α1＜α2;

3)若h(α1)＞h(α2)，則α1大于α2，記為α1＞α2.

定義5［4］設αj=(μaj，vaj)(j=1，2，…，n)為一組直覺模糊數，直覺模糊有序加權平均(IFOWA)算子是一個映射:IFOWA:Θn→Θ:

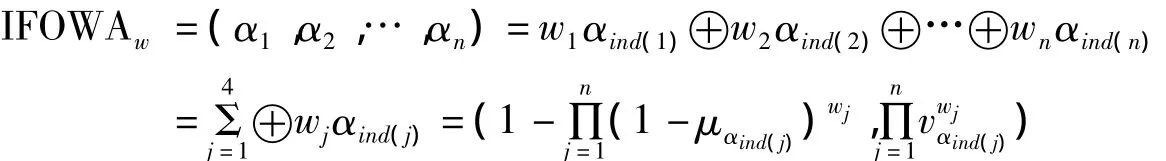
3 PIFOWA算子

對于某一多屬性決策問題，設屬性集C={c1，c2，…，cn}，屬性權重未知且屬性間具有優先級別關系c1＞c2＞…＞cn，即當i＜k時，有ci的優先權大于ck的優先權，設方案x在屬性cj下的屬性值cj(x)為一組直覺模糊數cj(x)=αj=(μαj，vαj)(j=1，2，…，n).

定義6 設{α1，α2，…，αn}為一組直覺模糊數，則屬性間具有優先級別的直覺模糊OWA(PIFOWA)算子是一個映射:PIFOWA:Θn→Θ，使得

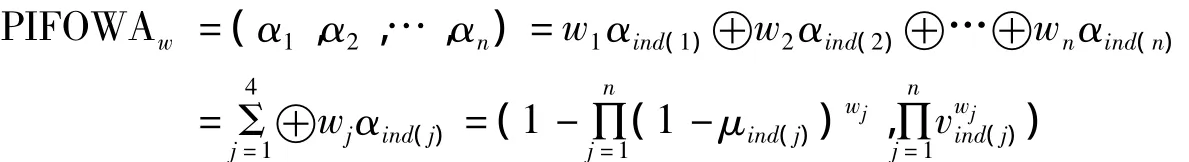
其中αind(j)為(α1，α2，…，αn)中第j大的元素，w=(w1，w2，…，wn)T是與PIFOWA算子相關聯的加權向量，滿足

下面我們給出與PIFOWA算子相關聯的加權向量的具體求法:

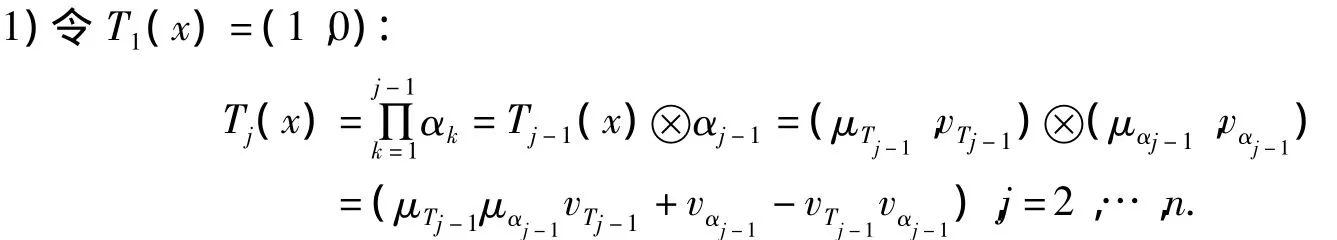
3)應用確定OWA算子權重的BUM函數來確定PIFOWA算子的權重w=(w1，w2，…，wn)T.設αind(k)為屬性值(α1，α2，…，αn)中第k大的元素，rind(k)為αind(k)對應的屬性權重，令R0=0，Rj=kΣ=

j1rind(k)，j =1，2，…，n，則:

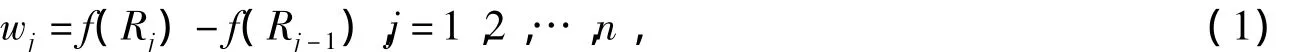
其中f:［0，1］→［0，1］是一個BUM函數.

4)若IFOWA算子權重w=(w1，w2，…，wn)T已知，此權重向量只對集結屬性值的位置加權，并沒有考慮屬性間的優先級別關系，為使集結更合理，我們用Torra給出的方法對該權重向量進行了修正.

Torra(1997)［10］、Torra和Narukawa(2007)［11］給出了一個分段線性函數，令:

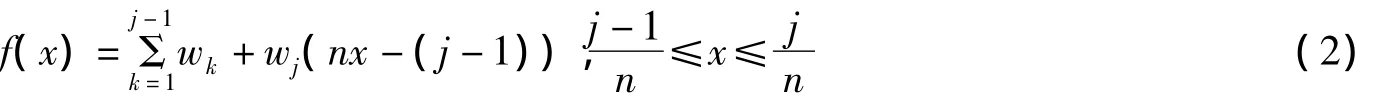
則修正后的權重為:

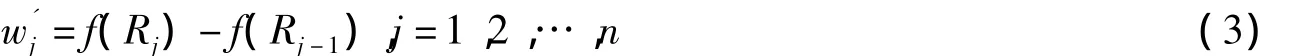
然后再利用PIFOWA算子進行集結:

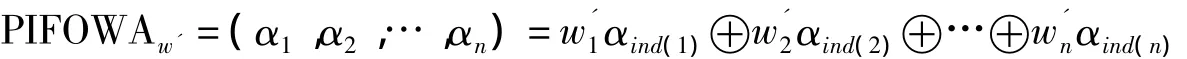
PIFOWA算子具有的性質有:

性質1 設αj=(μαj，vαj)(j=1，2，…，n)為一組直覺模糊數，若所有直覺模糊數αj(j=1，2，…，n)是相等的，即αj=α(j=1，2，…，3)，則:

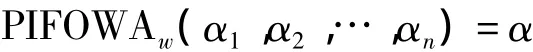
性質2 設αj=(μαj，vαj)(j=1，2，…，n)為一組直覺模糊數，且α－=(mjin{μαj}，mjin{vαj})，α+= (mjin{μαj}，mjin {vαj})，則:

例3.1 設屬性集為c={c1，c2，c3，c4}，屬性間有優先關系:c1＞c2＞c3＞c4，方案x在各屬性下的屬性值為直覺模糊數:α1=(0.5，0.3)，α2=(0.1，0.4)，α3=(0.8，0.1)，α4=(0.3，0.4).

先求與PIFOWA算子相關聯的加權向量，根據步驟1)可得:

取β=0.5，根據步驟2)得由優先關系確定的屬性權重向量r=(r1，r2，r3，r4)T，其中

由此可得歸一化的屬性權重

r1=0.4892;r2=0.2935;r3=0.1150;r4=0.1023.

由得分函數得:s(α1)=0.3，s(α2)=－0.3，s(α3)=0.7，s(α4)=－0.1，由此可得:α3＞α1＞α4＞α2.因此，ind(1)=3，ind(2)=1，ind(3)=4，ind(4)=2;αind(1)=(0.8，0.1)，αind(2)=(0.5，0.3)，αind(3)=(0.3，0.4)，αind(4)=(0.1，0.4);rind(1)=0.115，rind(2)=0.7892，rind(3)=0.1023，rind(4)=0.2935.

取BUM函數為f(x)=x2，由R0=0，R1=rind(1)=0.115，R2=rind(1)+rind(2)=0.6042，R3=rind(1)+ rind(2)+rind(3)=0.7065，R4=rind(1)+rind(2)+rind(3)+rind(4)=1及公式(1)得與PIFOWA算子相關聯的權重:w1=0.0132，w2=0.3519，w3=0.1342，w4=0.5009.

故方案x的綜合屬性值為:

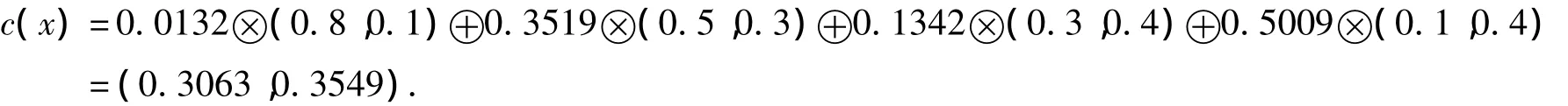
若已知IFOWA算子的權重為w=(0.155，0.345，0.345，0.155)T，利用(2)式得分段函數:

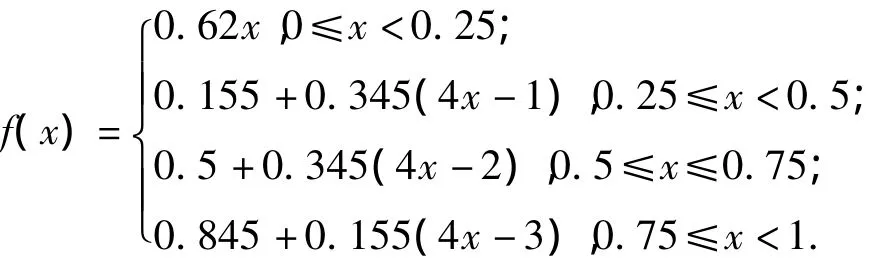
由R0=0，R1=0.2642，R2=0.6645，R3=0.6805，R4=1得:

由公式(3)式得修正后的權重為:w1=0.1746，w2=0.5524，w3=0.0221，w4=0.2509.

故方案x的綜合屬性值為:

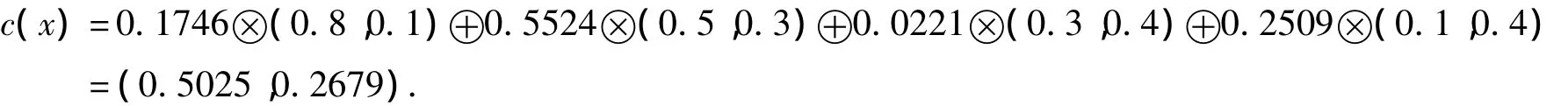
4 基于PIFOWA算子的直覺模糊多屬性決策方法

研究的直覺模糊多屬性決策問題描述為:設屬性集C={c1，c2，…，cn}，屬性權重未知且屬性間具有優先級別關系c1＞c2＞…＞cn，即當i＜k時，有ci的優先權大于ck的優先權，設方案x在屬性cj下的屬性值cj(x)為一組直覺模糊數cj(x)=αj=(μαj，vαj)(j=1，2，…，n).

基于PIFOWA算子的直覺模糊多屬性決策方法與步驟可歸納如下:

第一步:結合所給的數據信息，根據實際情況預先選定參數β，根據第3節中的步驟1)、2)、3)，計算與集結算子PIFOWA相關的權重向量w.若PIFOWA算子權重已知，則利用步驟4)進行修正.

第二步:根據PIFOWA算子定義計算方案xi(i=1，2，…，n)的綜合評價值c(xi)(i=1，2，…，n)，得到的綜合評價值仍為一個直覺模糊數.

第三步:利用得分函數計算方案xi(i=1，2，3，…，n)的綜合評價值的得分值s(xi)，對方案xi(i=1，2，3，…，n)進行排序并擇優(如果有兩個方案xi和xj的得分值相等，即s(xi)=s(xj)，則需要根據精確函數計算其精確度h(xi)和h(xj)，然后利用h(xi)和h(xj)對方案xi和xj進行排序).

5 結論

本文解決了在直覺模糊環境下，屬性間有優先關系的多屬性決策問題.給出了PIFOWA算子的定義，并給出了確定該算子權重的方法，在計算屬性權重rj時可發現r1≥r2≥…≥rn，符合屬性間的優先級別關系.利用該算子集結直覺模糊數的基本思想是:具有較低優先級別的屬性其權重由方案在較高優先級別屬性下的屬性值來確定，這樣可使方案的集結結果充分考慮屬性間的優先級別關系，使集結結果更合理.

［1］Atanassov K T.Intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1986，20:87－96.

［2］Atanassov.K.Intuitionistic fuzzy sets:theory and applications［M］.Heidelberg:Physica－VerLag，1999.

［3］Xu Z S，Yager R R.Some geometric aggregation operators based on intuitionistic fuzzy sets［J］.International Journal of General Systems，2006，35:417－433.

［4］Xu Z S.Intuitionistic fuzzy aggregation operators［J］.IEEE Transaction on Fuzzy Systems，2007，15:1179－1187.

［5］Yager R.R.Modeling prioritizedmulticriteria decisionmaking［J］.IEEE Transactionson Systems，Man，and Cybernetics－Part B:Cybernetics，2004，34(6)，2396－2404.

［6］Yager R.R.Prioritized aggregation operators［J］.International Journal of Approximate Reasoning，2008，48(1):263－274.

［7］Yager R.R.Prioritized OWA aggregation［J］.Fuzzy Optimal Decision Making，2009，8(3):245－262.

［8］Chen SM，Tan JM.Handling multicriteria fuzzy decision－making problems based on vague set theory［J］.Fuzzy Sets and Systems，1994，67:163－172.

［9］Hong D H，Choi C H.Multicriteria fuzzy decision－making problems based on vague set theory［J］.Fuzzy Sets and Systems，2000，114:103－113.

［10］Torra V.The weighted OWA operator［J］.International Journal of Intelligent Systems，1997，12，153－166.

［11］Torra V.，Narukawa Y.Modeling decisions:Information fusion and aggregation operators［M］.Berlin:Springer，2007.