傳統型和L型麥弗遜懸架運動學仿真

宋江濤，馮金芝，鄭松林

SONG Jiang-tao, FENG Jin-zhi, ZHENG Song-lin

（上海理工大學 機械工程學院，上海 200093）

0 引言

懸架系統是現代汽車上的重要總成之一，麥弗遜懸架則是現代汽車上最常用的前懸架結構形式。其結構簡單、占用空間小、響應較快、制造成本低。懸架運動特性的優劣關系到汽車操縱穩定性、舒適性、轉向輕便性和輪胎使用壽命。車輪定位參數在行駛過程中會不斷變化，這些車輪定位參數的變化對汽車的操縱穩定性會產生很大影響。因此系統地開展懸架運動學和動力學的研究，并由此指導現代汽車懸架的開發設計，提高汽車的行駛穩定性，是現代汽車懸架研究開發中重要課題。

在懸架開發設計過程中，運用虛擬樣機技術獲得最優化和創新的設計模型，是一種高效的研發手段。虛擬樣機VP(Virtual Prototype)技術是在CAD/CAM/CAE技術及多體系統MBS(Multi-body System)動力學基礎上發展起來的系統級的產品建模、仿真與分析技術，自產生后就迅猛發展，并得到多方面的應用，在車輛產品設計與性能分析方面，引起極大關注[1~3]。

本文利用多體動力學理論，在虛擬樣機仿真軟件ADAMS/Car中建立了傳統型和控制臂縱向“0偏移”L型麥弗遜懸架的運動學仿真模型。通過仿真計算比較了這兩種形式懸架對汽車操縱穩定性的影響。

1 傳統麥弗遜懸架模型

對麥弗遜式懸架系統的實際結構進行整合和運動特性進行分析，如圖1所示，模型中包括的零件有軸套、三角形控制臂、橫拉桿、轉向節、輪轂、螺旋彈簧、減震器和轉向節立柱。通過分析整合零件之間的相對運動關系，確定懸架模型中各零件之間的約束關系。圖2為某型車麥弗遜前懸架模型拓撲結構簡圖，約束以方框“□”標出，其約束列表如表1所示。

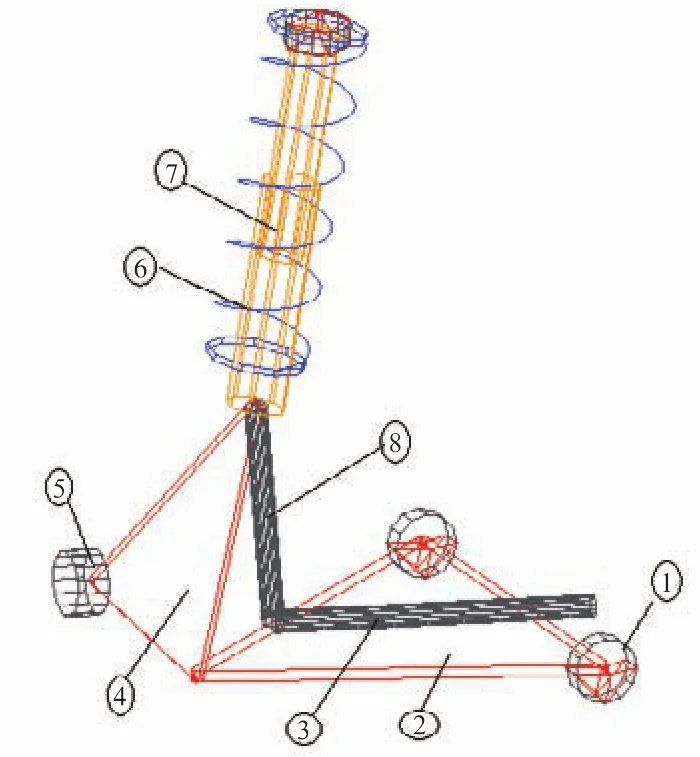
圖1 傳統麥弗遜式懸架簡圖

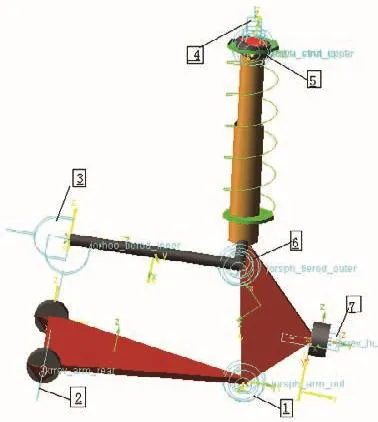
圖2 傳統麥弗遜式懸架拓撲簡圖

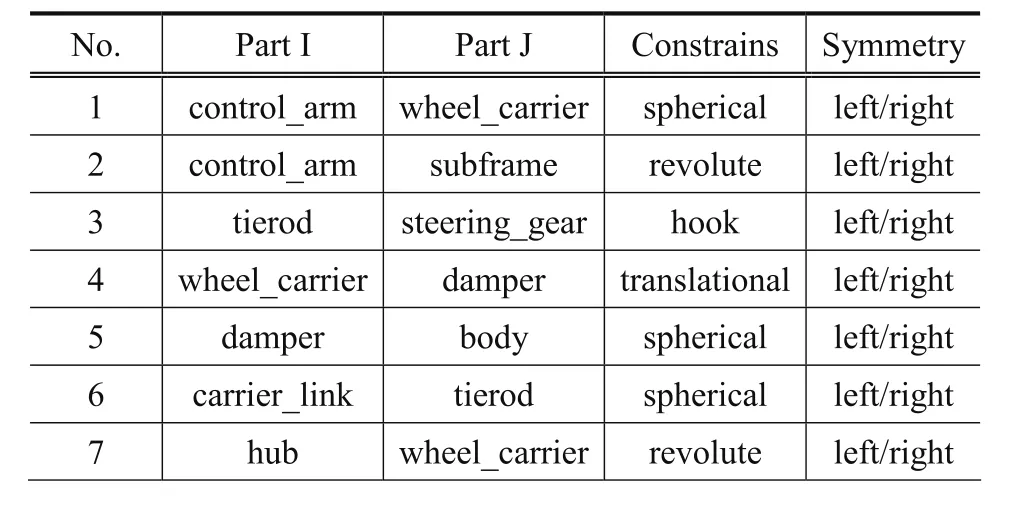
表1 懸架模型約束描述

懸架系統多體模型主要由零件、約束和力（仿真模型中彈簧和減震器作為力元素處理）構成。模型中零件的幾何（尺寸）定位參數、質量特性參數、各聯接襯套的力學特性參數以及彈簧與減震器的力學特性參數，均通過研究課題中數據所得。

2 控制臂縱向“0 偏移”L 型麥弗遜懸架模型

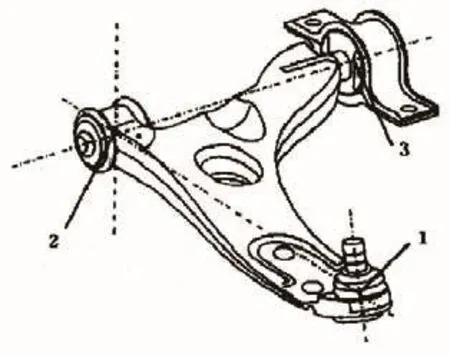
圖3 縱向“0 偏移”L 型控制臂

如圖3所示控制臂縱向“0偏移”L型麥弗遜懸架是在傳統麥弗遜懸架的基礎上，將三角形控制臂與車身相連的前端點2向后移，即控制臂前部連接襯套的中心在汽車縱向接近于“0偏移”。從車輪傳遞到球銷的側向力通過L型控制臂前連接軸套直接傳遞到副車架(后連接軸套的影響很小)，這樣只需要通過設定前連接軸套的剛度來調節汽車的側向剛度[4]。由此可以建立控制臂縱向“0偏移”L型麥弗遜懸架運動學分析模型，圖4為控制臂縱向“0偏移”L型麥弗遜懸架的簡圖，圖5為運動學仿真模型。

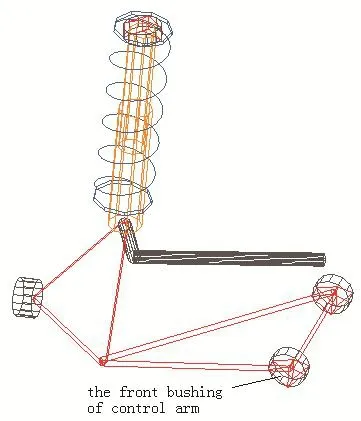
圖4 控制臂縱向“0偏移”L型麥弗遜懸架簡圖

圖5 控制臂縱向“0偏移”L型麥弗遜式懸架運動學仿真模型

在汽車通過有凹坑的路面引起在車輪接地點產生縱向力時，此縱向力繞控制臂球銷和前連接軸套的軸線形成縱向力矩，通過設定L型控制臂后連接軸套的剛度來控制該力矩，緩和路面帶來的沖擊使車輪產生縱向柔性。同樣，在汽車制動或加速時，由于慣性作用的質量轉移產生的下蹲和上抬也可以通過設定L型控制臂后連接軸套的剛度來控制，從而也改善了乘坐的舒適性[4]。然而，由于麥弗遜懸架的主銷軸線位置在減振器與車身連接鉸鏈中心和控制臂與轉向節連接鉸鏈中心的連線上，因此控制臂前端點后移而在控制臂球銷和前連接軸套的軸線形成縱向力矩會使主銷后傾角在汽車行駛過程中變化范圍有所增加[5]。

L型控制臂的設計，使汽車在側向和縱向的受力分別通過前、后連接軸套進行控制，使需要的側向剛度獨立于縱向柔性，使側向力和縱向力同時作用時相互間不發生耦合，避免了懸架臂共振的發生，從而提高了汽車行駛的平順性[4]。另外，L型控制臂的前后連接軸套剛度一般都設定為前硬后軟，在汽車轉向受到側向力時，有助于前輪形成負前束，增加不足轉向的趨勢，有利于提高汽車行駛的操縱穩定性[4]。

3 兩種懸架運動學仿真結果的對比

研究懸架的運動特性通常采用車輪跳動的分析方法，即通過使一側車輪或兩側車輪沿垂直方向跳動，計算分析由此引起的車輪定位參數、車輪轉角等的變化規律[6]。車輪的跳動量以滿載為基準，此次運動仿真采用雙側車輪同向激勵（Parallel Wheel Travel），取其跳動范圍為常用的-50～+50mm（0～-50mm表示下跳，0～50mm表示上跳），對比分析這兩種形式麥弗遜懸架的車輪外傾角、車輪前束、車輪轉角等的輪跳特性。

3.1 車輪外傾角

車輪外傾角是通過車輪中心的汽車橫向平面和車輪平面的交線與地面垂線的夾角，即由車前方看輪胎中心線與垂直線所成的角度，向外為正，向內為負，如圖6所示。

圖7為車輪外傾角隨車輪跳動的變化曲線。在通常設計中車輪都具有一定的外傾角,當車輪向上跳動時,外傾角一般向負值方向變化,而下落時向正的方向變化,這樣可以減小輪胎的磨損,提高汽車的操縱穩定性。一般車輪的外傾角的變化不宜太大,其范圍為- 3°～3°，在正常的跳動范圍內,外傾角的變化量應盡量小[7]。從圖8可以看出,在車輪跳動±50mm的行程內,傳統麥弗遜懸架的車輪外傾角的變化范圍為-1.29°～0.73°，而控制臂縱向“0偏移”L型麥弗遜懸架的外傾角變化范圍為-1.17°～0.67°，在一定程度上有所改善，從而有利于保證汽車的操縱穩定性。

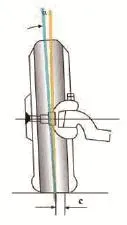
圖6 外傾角示意圖

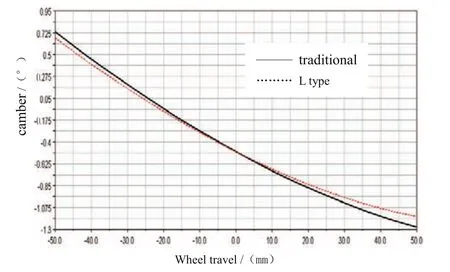
圖7 車輪外傾角隨車輪跳動的變化曲線

3.2 車輪前束角

車輪有了外傾角后，在滾動時就類似于滾錐，從而導致兩側車輪向外滾開。由于轉向橫拉桿和車橋的約束車輪不致向外滾開，將在地面上出現邊滾邊向內滑的現象，從而增加了輪胎的磨損。為了避免這種由于圓錐滾動效應帶來的不良后果，將兩前輪適當向內偏轉，即形成前輪前束[8]。

汽車兩側車輪的前邊緣距離B小于后邊緣距離A，后邊緣距離A與前邊緣距離B之差為車輪前束。當汽車的前邊緣小于汽車的后邊緣時，車輪前束為正，反之則為負。車輪的水平直徑與車輛縱向對稱平面之間的夾角為前束角。如圖8所示。

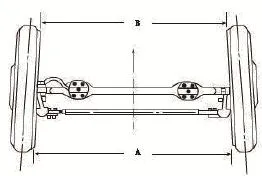
圖8 前束角示意圖

圖9為車輪前束角隨車輪跳動的變化曲線。車輪前束可以消除由于車輪外傾引起的輪邊滑現象，減少輪胎的磨損。另外,為了不因輪胎的側偏而使磨損加劇、滾動阻力增大以及直線行駛能力受到損害，無論在車輪下落還是上跳時都不應出現大的前束值變化。汽車在運動過程中前束會發生變化，如果在車身側傾或者由于側向力作用而上跳的車身外側前輪產生負前束，而下落的內側前輪產生正前束，車橋具有不足轉向特性，提高操縱穩定性[9]。總之，在車輪跳動時,車輪前束角盡可能不變或者變化較小。從圖9可以看出,在車輪跳動±50mm的行程內,傳統麥弗遜懸架的車輪前束角的變化范圍為-1.07°～0.67°,而控制臂縱向“0偏移”L型麥弗遜懸架的前束角變化范圍為-0.79°～0.50°，車輛操縱穩定性得到很大的提高。

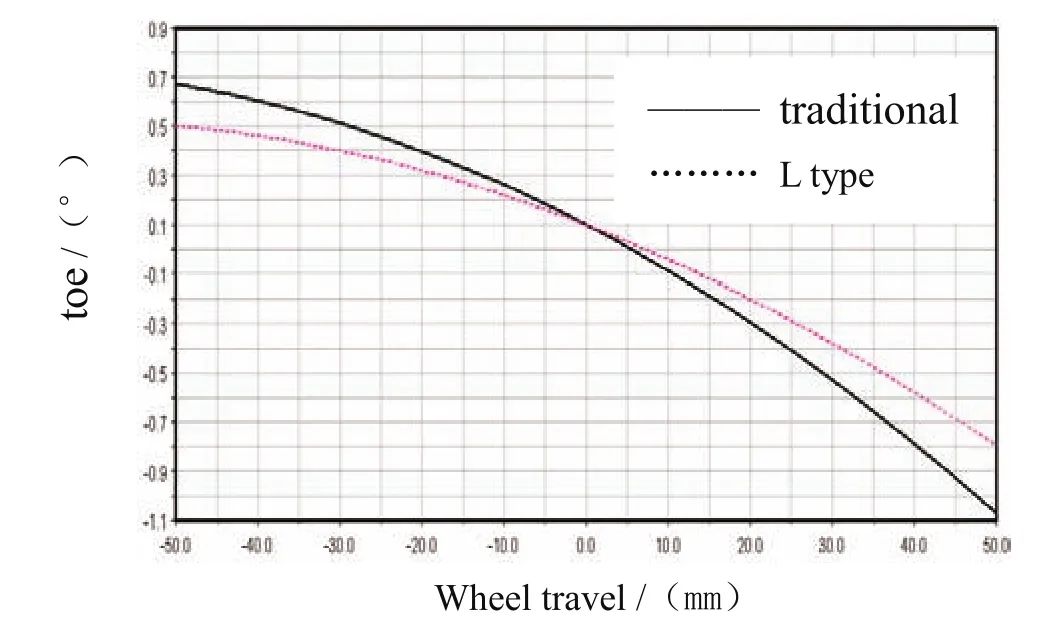
圖9 車輪前束角隨車輪跳動的變化曲線

3.3 主銷后傾角

主銷后傾角即主銷軸線與地面垂直線在汽車縱向平面內的夾角。向垂線后面傾斜的角度稱為正后傾角；向前傾斜的角度稱為負后傾角。通常汽車行駛過程中，主銷后傾角應為正值。如圖10所示。

圖10 主銷后傾角示意圖

圖11為主銷后傾角隨車輛跳動的變化曲線，在車輪跳動±50mm的行程內,傳統麥弗遜懸架的主銷后傾角的變化范圍為1.63°～2.29°,而控制臂縱向“0偏移”L型麥弗遜懸架的主銷后傾角變化范圍為1.54°～2.37°，主銷后傾角變化范圍有所增加。一般主銷后傾角越大，主銷后傾拖距也越大，則回正力矩的力臂越大，因此回正力矩也就越大，操縱穩定性就越好。但是回正力矩不宜過大，否則在轉向時為了克服此力矩，駕駛員必須在方向盤上施加較大的力（方向盤發沉）。一般要求后傾角具有隨車輪上跳而增加的趨勢，這樣可以抵消制動點頭時后傾角減小的趨勢。轎車主銷后傾角一般為：前置前驅0°~3°；前置后驅3°~10°[9]。

圖11 主銷后傾角隨車輪跳動的變化曲線

3.4 主銷內傾角

從汽車的正前方看，主銷（或轉向軸線）的上端略向內傾斜一個角度，稱為主銷內傾。嚴格的定義為主銷軸線與地面垂直線在汽車橫向平面內的夾角稱為主銷內傾角。主銷軸線上側向內傾時為正，反之為負。如圖12所示。

圖12 主銷內傾角示意圖

圖13為主銷內傾角隨車輛跳動的變化曲線，在車輪跳動±50mm的行程內,傳統麥弗遜懸架的主銷內傾角的變化范圍為8.11°～10.40°,而控制臂縱向“0偏移”L型麥弗遜懸架的主銷內傾角變化范圍為8.18°～10.28°，主銷內傾角的變化范圍略有減小。主銷內傾有利于減小主銷橫向偏移距,從而可減少轉向時駕駛員加在方向盤上的力,使轉向操縱輕便,同時也可減少從轉向輪傳到方向盤上的沖擊力。但主銷內傾角不宜過大，一般在7°~13°之間，同時主銷偏移距也希望取較小的數值，否則轉向時，在車輪繞主銷轉動的過程中，輪胎與路面之間產生較大的滑動，增加輪胎與路面間摩擦阻力，這不僅使轉向變重，而且加速輪胎的磨損。一般認為理想情況下在車輪上跳時，主銷內傾角的增加應盡量減小，以避免主銷內傾角變化過大[10]。

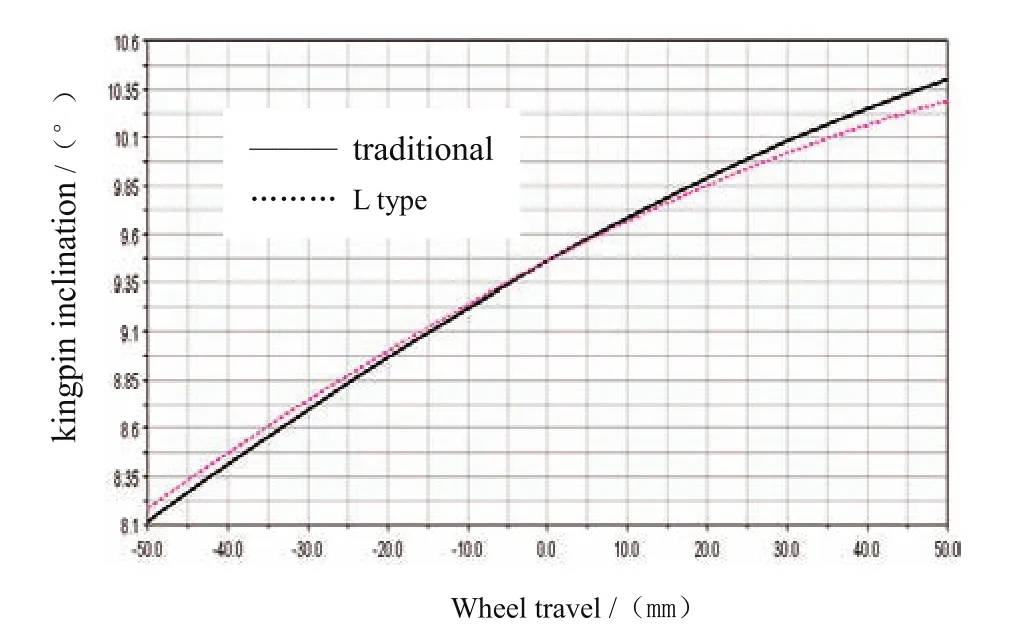
圖13 主銷內傾角隨車輪跳動的變化曲線

3.5 車輪轉向角、抬頭量和點頭量

圖14、圖15和圖16分別為車輪轉向角、點頭量和抬頭量隨車輪跳動的變化曲線。

從圖中可以看到，在車輪跳動±50mm的行程內,傳統麥弗遜懸架的車輪轉向角的變化范圍為-0.67°～1.07°,而控制臂縱向“0偏移”L型麥弗遜懸架的主銷后傾角變化范圍為-0.50°～0.79°，左右輪轉角變化相反。在車輪跳動過程中，方向盤固定，由于轉向拉桿的作用，左右車輪會產生繞主銷的轉動，從而使左右車輪產生轉向角。一般要求將該轉角控制在一定的范圍內，否則不僅影響汽車的操縱穩定性，而且會加劇輪胎的磨損；控制臂縱向“0偏移”L型麥弗遜懸架比傳統麥弗遜懸架在抬/點頭量都有一定程度的降低，即汽車操縱穩定性和乘坐舒適性都有所改善。

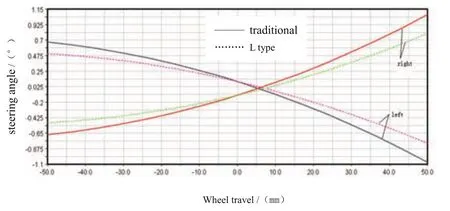
圖14 車輪轉向角隨車輪跳動的變化曲線

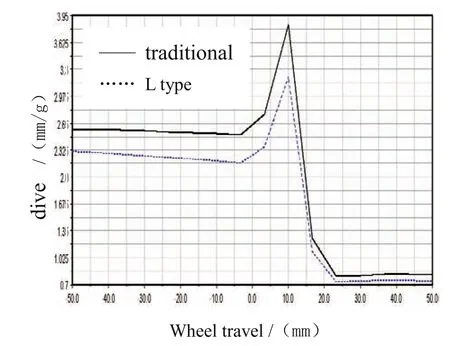
圖15 點頭量隨車輪跳動的變化曲線

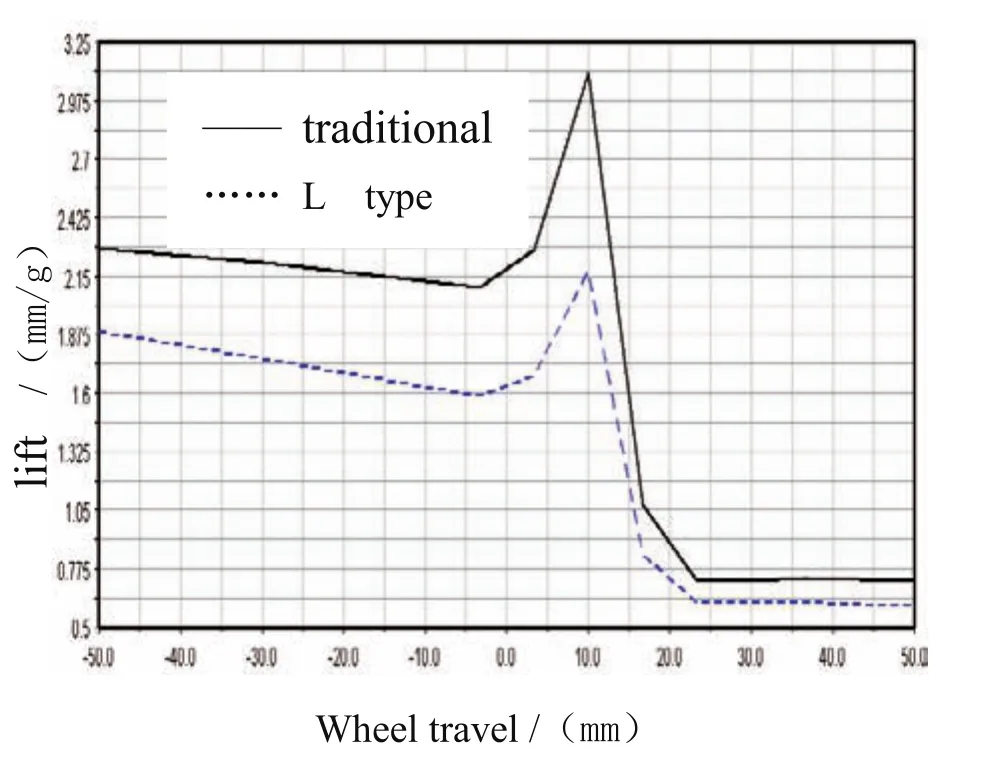
圖16 抬頭量隨車輪跳動的變化曲線

4 結論

本文利用多體動力學理論,在虛擬樣機仿真軟件ADAMS/Car中建立了傳統三角形控制臂麥弗遜懸架和改進后控制臂縱向“0偏移”L型麥弗遜懸架多體模型，進行了雙側車輪同向激勵輸入下的運動學仿真計算。

1）通過運動仿學真分析，揭示了傳統麥弗遜懸架和控制臂縱向“0偏移”L型麥弗遜懸架的車輪定位參數、車輪轉向角以及抬/點頭量一般運動規律；

2）通過對比兩種型式麥弗遜懸架的運動學仿真結果，可知控制臂縱向“0偏移L型麥弗遜懸架更有利于提高汽車的操縱穩定性與平順性；

3）本文研究表明，控制臂與車身連接位置的適當變化在一定程度上有利于改善汽車的操縱穩定性。運動學性能只是汽車整體性能的一部分，L型麥弗遜懸架是否可以取代傳統型麥弗遜懸架，需要進行更深入的全面研究。

[1]陳立平,張云清,任偉群,覃剛,等.機械系統動力學分析及ADAMS應用教程[M].北京:清華大學出版社,2005.

[2]王國強,張進平,馬若丁.虛擬樣機技術及其在ADAMS上的實踐 [M].西安:西北工業大學出版社,2002.

[3]陳德民,槐創鋒,張克濤.精通ADAMS 2005//2007虛擬樣機技術[M].北京:化學工業出版社,2010.

[4]艾維全,高世杰,王承,廖芳.麥弗遜式前懸架的設計改進及分析[J].上海汽車,2004,8:26-28.

[5]郭孔輝.汽車操縱動力學[M].長春:吉林科學技術出版社,1991.

[6]趙立微,基于K&C試驗的懸架特性分析與試驗優化[D].吉林大學,2008.

[7]陳家瑞,馬天飛.汽車構(下)[M].北京:人民交通出版社,2006,5.

[8]劉偉忠.基于虛擬樣機技術的某車懸架K&C特性仿真分析及硬點優化[D].吉林大學,2009.

[9]Hazem Ali Attia Numerical Kinematic Analysis of the Standard Macpherson[J].KSME International Journal,2003,17(12):1961-1968.

[10]J.Liu,D.J.Zhuang,F.Yu,L.M Lou.Optimized design for a Macpherson strut suspension with side load springs[J].International Journal of Automotive Technology,2008,9(1):29-35.