原狀軟粘土各向異性及其對工程影響研究

嚴佳佳，李伯安，陳利明，周 建，管林波

（1.浙江大學巖土工程研究所，浙江 杭州 310058；2.浙江省水利水電勘測設計院，浙江 杭州 310002；3.寧波水利水電規劃設計研究院，浙江 寧波 315016)

0 引言

軟粘土地基上工程施工，如路堤的填筑、基坑開挖等，都會引起地基土體內應力狀態改變，其中很重要的一點就是土體的大主應力方向發生顯著改變。Zdravkovi?[1]對一軟粘土地基上的試驗路堤進行了有限元分析，與實測數據進行對比，結果表明利用能反應土體強度各向異性的 MIT-E3模型計算得到路堤極限高度與實際的高度吻合較好，而假設土體為各向同性的修正劍橋模型計算得到的路堤極限高度則遠大于實際的高度。近一步分析可以發現路堤下土體破壞面上大主應力方向角都有明顯偏轉(圖 1)。Bjerrum[2]對路堤下的地基和軟粘土地基中的基坑開挖進行了研究，認為土體各向異性是控制土體穩定性的主要因素之一。此外，近海工程結構的地基基礎由于承受波浪、潮汐作用，受土體各向異性影響也很大。后期研究發現土體在經歷交通荷載、波浪荷載[3]等作用時都有一個共同的特點，即主應力軸發生旋轉。土體在沉積過程及后期應力作用下會產生明顯各向異性[4]。材料各向異性是指材料特性在不同方向表現不同的性質。主應力軸旋轉這類應力路徑使土體應力應變特性發生變化是土體材料各向異性的表現，歸根結底還是屬于土體材料各向異性的研究范疇。目前為止還沒有很實用的土體本構模型可以準確描述土體的實際工程性質，很大程度上是因為這些模型沒有很好考慮土體的一些基本特性,如應力―應變―強度各向異性，從而處理實際工程問題時很難考慮土體各向異性的影響。已有研究結果表明土體各向異性的特性對很多實際工程(尤其是地基土體中存在主應力軸旋轉情況)有很大影響。因此有必要研究主應力軸旋轉這類應力路徑下土體原生各向異性的變化及表現。已有的研究成果大多只針對重塑土(Symes[5-6]，Zdravkovi?[4])，對原狀土（尤其是原狀軟粘土）進行的研究還很少。

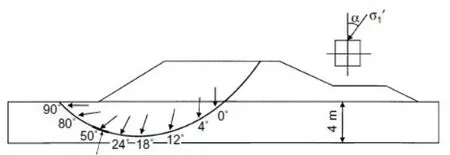
圖1 路堤下土體破壞面上大主應力的方向角(據文獻[1])Fig.1 Directions of major principal stress on failure surface of the soil under pavement (from reference [1]).

本文利用浙江大學 5 Hz空心圓柱扭剪儀(HCA)，通過設置不同的應力路徑對杭州原狀軟粘土進行試驗研究。針對對主應力軸靜態旋轉條件下原狀軟粘土的應力應變特性以及大主應力方向角α和中主應力系數b對原狀軟粘土各向異性的影響進行研究，分析原狀軟粘土應力―應變―強度各向異性及其對實際工程的影響，通過試驗研究分析常規的不考慮主應力軸旋轉影響的設計是否經濟可靠。

1 試驗方案

1.1 試驗儀器及樣品

本文研究選用的試驗儀器為浙江大學 5 Hz空心圓柱扭剪儀以及常規三軸儀。空心圓柱扭剪儀可以對空心試樣施加獨立控制的外壓Po、內壓Pi、軸力W和扭矩MT，可以實現大主應力軸連續旋轉的應力路徑，相比常規三軸儀、真三軸儀、直剪儀等，可以更好地研究大主應力方向角、中主應力等因素對土體應力應變特性的影響，更適合于研究土體的各向異性。而常規三軸儀主要用來做一些補充性的對比試驗。

試驗用土為取自杭州某基坑工地的原狀粘土。取土深度在開挖面下約7 m處，地下水位于地面以下 1 m。比重 G=2.74；孔隙比 e=1.78；含水率w=53.4%；濕密度ρ=1.77g/cm3；飽和度98.4%。使用專用切土器將土樣制備成200 mm×100 mm×60 mm（高度×外徑×內徑）的空心圓柱試樣，具體制作過程參見文獻[7]。

1.2 試驗方案

為研究大主應力方向角和中主應力系數等參數對土體各向異性的影響，設計了下列試驗：主應力軸定向剪切試驗（T）、主應力軸純旋轉試驗（R），同時還補充了常規三軸試驗與空心圓柱扭剪儀的試驗結果進行對比驗證。R、T系列的試驗應力路徑如圖2所示。試驗過程中空心試樣在HCA壓力室內反壓飽和之后，在150 kPa的有效等向圍壓(外壓200 kPa，內壓200 kPa，反壓50 kPa)下進行固結，參考《土工試驗規程》(SL237-1999)的要求，取1 h排水量不超過0.1 cm3作為固結完成標準。完成固結后，通過控制大主應力方向角α、中主應力系數 b、平均主應力p和剪應力q來實現相應的應力路徑，具體試驗參數見表1，文中各參數定義參見文獻[7]。

常規三軸試驗的試樣則按不同大主應力方向切取，即試樣軸線方向與豎直方向呈一定角度,分別切取了 0°、20°、45°、60°和 90°等 5 個方向的試樣,進行了圍壓為100 kPa和200 kPa的試驗。

2 試驗結果分析

2.1 主應力軸定向剪切試驗

主應力軸定向剪切的試驗應力路徑如圖 2中OAB所示，試樣等向固結之后，保持中主應力系數b，剪應力q和平均主應力p不變，旋轉大主應力方向到達設定值（即表 1中α值），然后再保持大主應力方向不變，只增大剪應力q直至試樣發生破壞。本文分別進行了b=0和b=0.5兩組定向剪切試驗。

通過試驗結果可以研究原狀軟粘土抗剪強度的各向異性。在偏應力坐標內T1（b=0）和T2（b=0.5）系列試驗過程中的實際應力路徑分別如圖3(a)、(b)所示。偏應力坐標中應力路徑的屈服點（圖 3(a)）到原點的距離即為應力莫爾圓的半徑（也即土的抗剪強度），與橫坐標正向的夾角即為兩倍大主應力方向角2α。

圖2 試驗應力路徑Fig.2 Stress paths in tests.

表1 T系列試驗方案

圖3 主應力軸定向剪切試驗實際應力路徑Fig.3 Stress paths in the shear tests with principal stress axie rotation(b=0,b=0.5).

從圖3(a)中可以看到偏應力坐標內各個方向土體的抗剪強度都不相同，α=45°時最大，qmax=68.87 kPa，該結果與通常認為的土體與水平方向成45°角方向強度最低的結論并不一致，但本文的兩組試驗結果一致，說明水平方向不是試驗用土的沉積方向。α＜45°時，隨著主應力軸傾斜角度的增大，抗剪強度也逐漸增大；α＞45°時，隨著大主應力軸傾斜角度增大抗剪強度逐漸減小。圖3(b)中土體各方向的抗剪強度基本都大于圖3(a)中的值（20°和50°時除外），但變化趨勢基本一致(圖4)，抗剪強度最大值q=76 kPa也出現在α=45°方向上。可見杭州原狀軟粘土的抗剪強度存在強烈的原生各向異性，各方向抗剪強度值雖然受中主應力系數影響，但各方向剪應力峰值變化趨勢是一致的（圖4），說明定向剪切應力路徑下土體原生各向異性對土體抗剪強度的各向異性起控制作用，而后期施加應力對抗剪強度各向異性的影響很小。由常規三軸壓縮試驗結果得到ε1～(σ1?σ3)/2壓縮曲線，若以E50（應力為(σ1?σ3)/2最大值一半時所對應點的割線模量）代表土體的變形模量[8]，則原狀軟粘土各個方向的變形模量可由各自的壓縮曲線得到，具體值見表 2。從表2中可見原狀軟粘土各個方向的變形模量不盡相同，但不同圍壓條件下各個方向變形模量總體的變化趨勢是相似的，圍壓增加時土體的變形模量也增加，與抗剪強度相一致，在 45°方向的變形模量也最大，這與空心圓柱扭剪試驗得到的結果也相吻合。所以原狀軟粘土的變形模量也存在很強烈的各向異性。

表2 三軸試驗壓縮曲線得到的壓縮模量

圖4 土體不同方向的剪應力峰值Fig.4 Peak shear stress in different directions.

2.2 主應力軸純旋轉試驗

主應力軸純旋轉試驗應力路徑如圖 2中路徑OCD所示，該試驗應力路徑分為兩個階段，第一階段為應力路徑中的OC段，即固結完成后保持大主應力為豎直方向不變，只增大剪應力 q；第二階段保持p、b、q參數不變，大主應力開始旋轉，即CD段，整個旋轉過程中土體所受的剪應力保持不變。圖5所示應力路徑中，試樣在大主應力軸為豎直方向時增大q到50 kPa，然后保持p、b、q參數不變，大主應力軸旋轉至α=200°。旋轉過程中三個主應力值保持不變，即土體各個方向所受的大主應力相同（因此圖6中沒有給出主應力的值），所以由試樣主應變的發展就可以研究原狀軟粘土在相同主應力作用下各個方向上的應變特性。

圖5 b=0.5時主應力軸純旋轉試驗實際應力路徑Fig.5 Stress path in test of R series with b=0.5.

主應力旋轉過程中應力和應變的變化情況如圖6、7所示。主應力軸旋轉過程中試樣所受的扭剪應力τθz在0°～45°范圍內為順時針方向，且逐漸增大，45°～90°范圍內逐漸減小，90°～180°范圍內的扭剪應力則為逆時針方向，但扭剪應力值的變化趨勢相同也是先增大后減小如圖6所示。即扭剪應力的變化有很明顯的規律和分界線，但從圖7中可以看到扭剪應變γzθ的變化就沒有很明顯規律和分界線。軸向應力、切向應力與相應應變的變化也類似。從圖中還可以看到應變和應力的發展是不同步的，應變的變化要滯后于應力的變化，如圖6中扭剪應力的峰值出現在 45°和 135°時，而扭剪應變的峰值則出現在70°和190°時。旋轉過程中主應力的值始終是不變的，但圖7中大主應變1ε還是隨著大主應力的旋轉而不斷積累。圖6還給出了大主應變方向角β隨大主應力方向角α的變化，旋轉開始時大主應變方向角β大于大主應力方向角α，到達α=35°后大主應變方向角β一直小于大主應力方向角α。所以土體在主應力軸旋轉條件下，應變并不是緊隨應力的變化而開展，即土體大主應變和大主應力的方向不共軸，這也是原狀軟粘土各向異性的重要體現。由圖3(b)（b=0.5）中可知大主應力方向為20°和30°時的定向剪切強度小于50 kPa，但是在圖5、7中可以看到在主應力軸轉到 20°和 30°時試樣并沒有屈服破壞，應變值也沒有很大的發展，所以在主應力軸連續旋轉條件下土體抗剪強度的各向異性發生了改變，這說明原狀軟粘土在該應力路徑作用下產生了次生各向異性，并且使土體的破壞模式發生了改變。

圖6 主應力軸純旋轉過程中應力和大主應變方向角β的變化情況Fig.6 Stress development during pure principal stress rotation and change of major principal strain direction(β).

圖7 主應力軸純旋轉過程中各應變分量的變化情況Fig.7 Strain compenent curves during pure principal stress.

3 土體各向異性對實際工程影響分析

Jardine&Smith[8]曾對一路堤填筑過程中路堤下土體的大主應力方向進行了有限元分析，通過計算得到路堤逐漸填高的過程中土體內大主應力方向發生了顯著變化，如圖8所示，離路堤中心線越遠，大主應力旋轉的角度越大。

由本文的試驗結果可以看到，軟粘土存在較強的原生各向異性，不同方向上土體的強度和變形模量都有很大的差異，而且主應力軸純旋轉時大主應變與大主應力的方向始終不一致。因此，若地基土中存在主應力軸旋轉的實際工程，設計時需要考慮土體各向異性對其影響，基于土體各向同性假設的設計可能偏于不安全。如圖8中第5點處在路堤填筑完成時水平方向的主應力是最大的，由于常規三軸試驗得到的都是大主應力方向為 0°時土體強度參數，所以一般設計時也認為大主應力方向就是豎向的。但是路堤下地基的實際大主應力方向一般都不是豎向的，以豎向的應力作為大主應力計算地基的強度以及沉降是低估了土體所受的最大主應力，對于水平向強度與變形模量都小于豎向的土體，這樣的設計結果將偏于不安全。從試驗結果中還可以發現當大主應力方向發生旋轉時,大主應變的方向并不隨大主應力方向同步變化,所以像路堤填筑這樣的實際工程中在上部填土的作用下,下部地基土的豎向變形并不一定是最大的,即僅僅控制地基豎向的沉降也偏于不安全，而且大主應力的純旋轉也可以引起顯著的應變積累，所以只考慮應力引起的應變也是不全面的。

圖8 計算點在路基內的分布（a）；路基內大主應力方向角隨路基高度的變化(b) (引自Jardine&Smith 1991)Fig.8 Distribution of the calculation points in the pavement(a); Direct-ions of principal stress change with the height of pavement(b).

4 結論

本文利用浙江大學空心圓柱扭剪儀對杭州原狀軟粘土進行了主應力軸旋轉試驗，在一定的應力路徑條件下結合實際工程對試驗結果分析得到以下結論。

(1) 中主應力系數對土體的抗剪強度有影響，但對抗剪強度的各向異性沒有顯著影響；

(2) 原狀軟粘土的強度、變形模量等材料特性都存在較強的各向異性，且在較低的應力水平下主要體現了土體的原生各向異性，應力施加引起的次生各向異性影響較弱；

(3) 主應力軸純旋轉過程中當剪應力大于土體的定向抗剪強度時在該方向上也可能不會發生屈服破壞；

(4) 大主應力方向純旋轉時大主應變的方向并不同步變化，且兩者方向始終不一致；

(5)實際工程中很大情況下都存在主應力軸旋轉現象，由于土體各向異性的存在，常規的不考慮土體各向異性影響的設計方法可能偏于不安全。

[1]Zdravkovi? L, Potts D M, Hight D W. The effect of strength anisotropy on the behaviour of embankments on soft ground[J]. Géotechnique,2002,52(6):447-457.

[2]Bjerrum L. Problems of soil mechanics and construction on soft claysand structurally unstable soils(collapsible,expansive and others)[C]//Proc.8th ICSMFE.Moscow:[s,n],1973,(3):109-159.

[3]Ishihara K.,Towhata I. Sand response to cyclic rotation of principal stress directions as induced by wave loads[J].Soils and Foundations,1983,23(4):11-26.

[4]Zdravkovi? L, Jardine R J. The effect on anisotropy of rotating the principal stress axes during consoled-ation[J]. Géotechnique,2001,51(1):69-83.

[5]Symes M J, Gens A, Hight D W. Undrained aniso-tropy and principal stress rotation in saturated sand[J]. Géotechnique, 1984,34(1):11-27.

[6]Symes M J, Gens A, Hight D W. Drained princi-pal stress rotation in saturated sand[J]. Géotechni-que, 1988,38(1):59-81.

[7]沈揚. 考慮主應力方向變化的原狀軟粘土試驗研究[D].杭州:浙江大學,2007.

[8]Jardine R J, Smith P R. Evaluating design parameters for multi-stage construction[C]//Proc: Geo-coast '91 International Conference.Yokosuka :Yokohama Port and Harbour Research Institute.1991:1197-202.

[9]龔曉南. 土力學[M]. 北京: 中國建筑工業出版社, 2002.