密勒定理及其應用

田社平,陳洪亮

(上海交通大學電子信息學院,上海 200240）

密勒定理及其應用

田社平,陳洪亮

(上海交通大學電子信息學院,上海 200240）

密勒定理在電路分析和設計中具有較廣泛的應用。本文結合當前電路教學實踐,就密勒定理表述、證明及其應用作進一步的討論。通過舉例說明了密勒定理的應用,給出了密勒定理的教學建議。作為電路規律的一種總結,利用密勒定理分析電路時具有事半功倍的作用,可加深學生對電路本質的理解。本文的討論可供從事電路教學的教師參考。

密勒定理;電路教學;電路分析

0 引言

電路定理是電路規律的總結。利用電路定理可簡化對電路的分析,起到事半功倍的作用。因此,電路定理是電路教學中的重要教學內容。在所有的電路教材中,都有常用電路定理的介紹,如疊加定理、戴維寧定理等,但也有一些電路定理在電路后續課程如“模擬電子技術”課程中常常用到,而在“電路理論”或“電路分析”課程中并未加以介紹。密勒定理就是其中之一。筆者在教學中發現,在電子電路類課程中往往直接利用密勒定理對電路進行分析或設計[1],而沒有對其進行表述或證明,而且應用密勒定理分析電路也有欠嚴密之處。這樣就出現了“電路理論”或“電路分析”課程中密勒定理不是教學內容,而在電路后續課程中又必須用到密勒定理的情況。

本文根據筆者的教學實踐,就密勒定理及其應用作進一步的討論,以供大家參考。

1 密勒定理的表述及其證明

密勒定理由M.Miller于1920年在研究真空電子三極管輸入阻抗時提出的,也稱為密勒效應,在電路教材具有多種表述形式[1-4]。其較為嚴謹的表述形式為如圖1(a)所示任一具有n個節點的電路。設節點1和節點2的電壓分別為u n1和u n2,如已知un2/un1=A,則圖1(b)電路與圖1(a)電路等效,其中R1=R/(1-A),R2=R/(1-1/A)。

圖1 密勒定理

文獻[5]給出了密勒定理的一種證明,本文將給出另外一種證明。將如圖1(a)所示電路等效為圖2所示電路,且使其中節點電壓u n(n+1)=0,則有

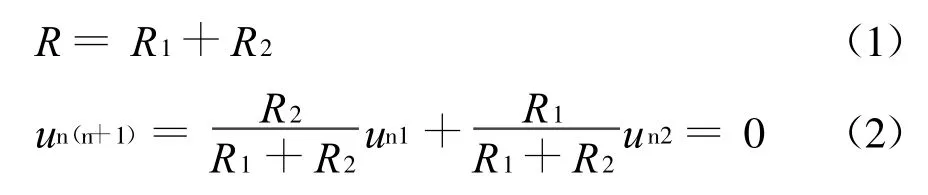
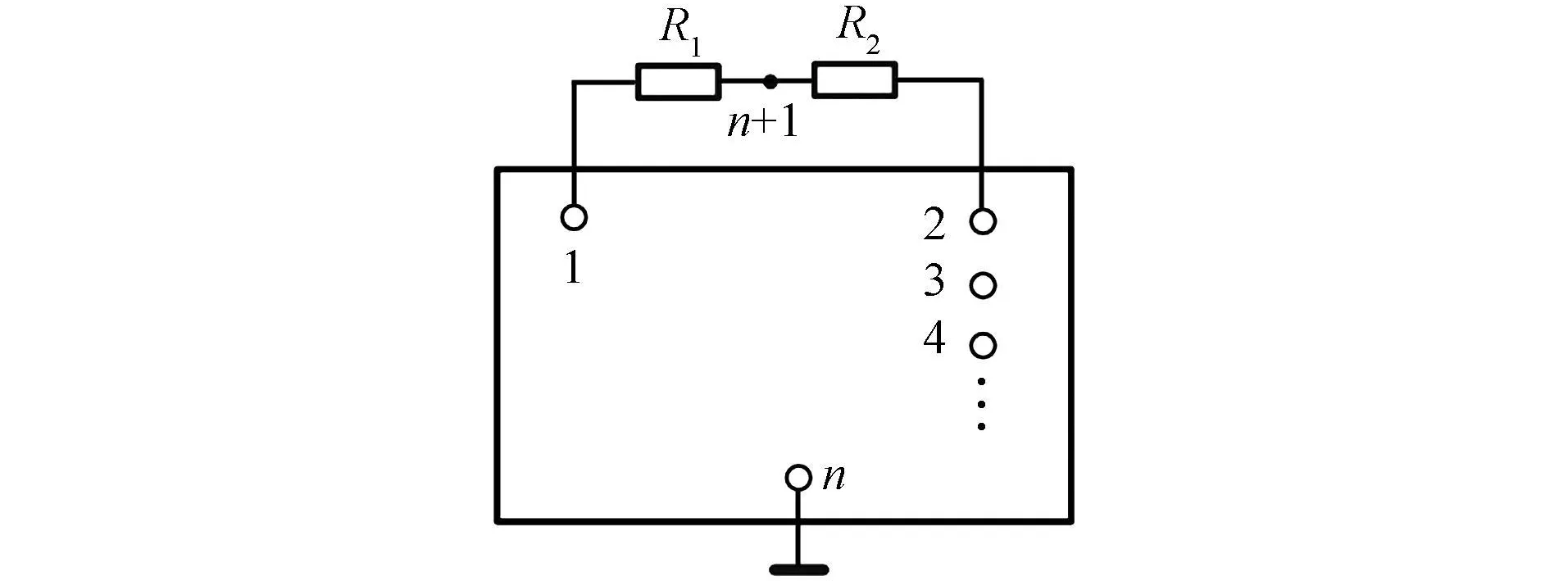
圖2 密勒定理的證明

而圖2所示電路與圖1(b)所示電路等效,由此定理得證。

從密勒定理的表述中可以看出,對于具有支路連接的兩個節點,如知道該兩節點的電壓,則利用密勒定理可消除兩節點的支路連接關系,從而使得電路的分析過程得到簡化。如果將圖1(a)中的節點1看作輸入節點,節點2看作輸出節點,則利用密勒定理可簡化輸入、輸出電阻的計算。

和其他電路定理類似,密勒定理在相量域或拉普拉斯變換域中都有相應的表現形式。

2 密勒定理的應用

密勒定理在電路分析中具有廣泛的應用,下面通過例子加以說明。

[例1]如圖3(a)所示電路,試求電壓u。

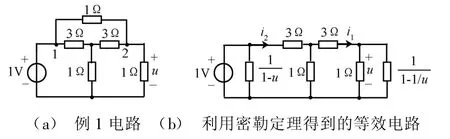
圖3 例1電路與等效電路

解本例可采用T-Π等效變換法或節點法或回路法求解,這里采用密勒定理求解。取電壓源的負極為參考節點,由密勒定理,u n1=1V,u n2=u,A=u,從而可得到圖3(b)所示等效電路,由KCL可得

將式(5)、式(6)代入式(7),可解得u=8V/17,與采用其他方法得到的結果相同。

由例1可見,即使節點電壓未知,也可采用密勒定理對電路進行分析。

[例2]試求圖4(a)所示電路的電壓比 H=u o/u S,設運算放大器的開環增益為 A,輸入電阻為無窮大,輸出電阻為零[6]。

圖4 例2電路與等效電路

解首先畫出圖4(a)所示電路的等效電路如圖4(b)所示,再由密勒定理可得圖4(c)所示等效電路。由圖4(c)可得

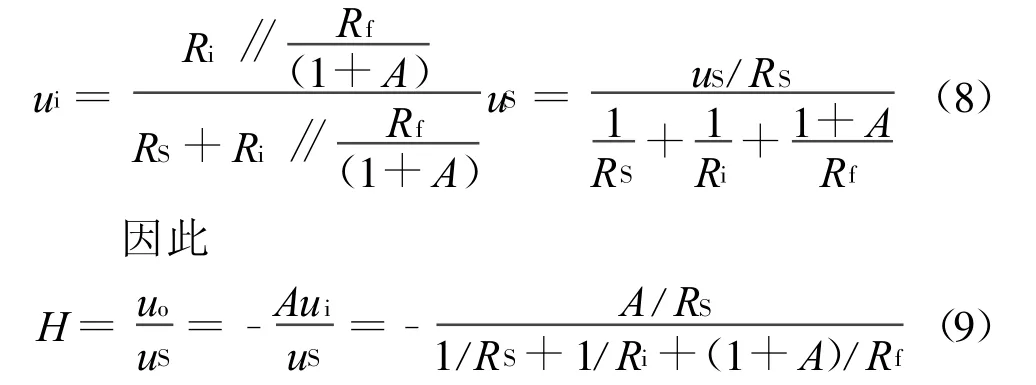
用其他方法分析例2電路都不如采用密勒定理來得簡潔。

[例3]圖5(a)所示為一電容倍增電路。試求輸入端口的等效電路。

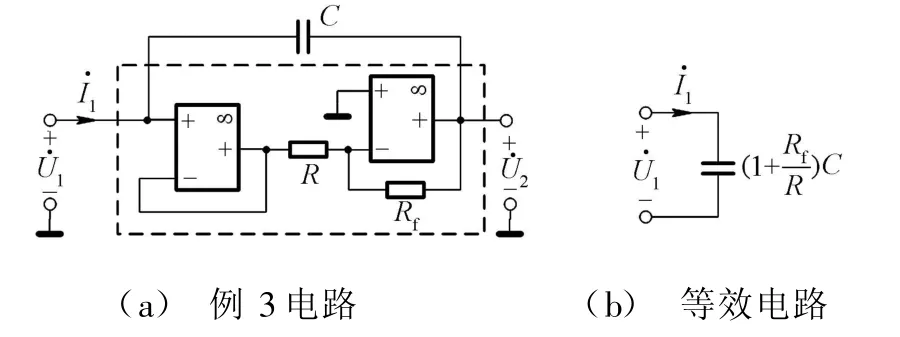
圖5 例3電路與等效電路

解由圖5(a)電路可知,電容兩端的電壓相量之比為A=﹒U2/﹒U1=1×(-Rf/R)=-Rf/R。再由密勒定理可知,電容支路等效于在輸入端跨接一個(1+R f/R)C的電容,在輸出端跨接(1+R f/R)C的電容。利用理想運算放大器的“虛斷”特性,可得出輸入端的等效電路如圖5(b)所示。

3 結語

密勒定理在電路分析和設計中具有較廣泛的應用,鑒于該定理在當前電路教學中的實際和筆者結合教學實踐認為,可在電路教學中適當介紹密勒定理及其應用。其理由在于:①密勒定理的內容十分簡潔,在理解上十分方便,作為電路教學內容不會占用過多學時;②存在相當多的電路問題可借助密勒定理來加以分析,其應用范圍較為廣泛;③作為電路規律的一種總結,利用密勒定理分析電路時具有事半功倍的作用,可加深學生對電路本質的理解,同時也可提高學生學習電路課程的興趣。

本文通過舉例說明了密勒定理在電路分析中的應用。其實,密勒定理在電路分析中還有更廣泛的應用,如在理想微分電路、電容補償、電阻補償和濾波器電路等方面,由于篇幅所限,不再贅述。筆者相信,隨著對密勒定理的進一步深入研究,肯定會挖掘出密勒定理在電路中的更有意義的價值。

[1] John M.M iller.Dependenceof the input impedan ce of a threeelectrode vacuum tube upon the load in the platecircuit.Scientific Papers of the Bu reau of Standards.1920,15(351):367-385

[2] 童詩白,華成英.模擬電子技術基礎[M].北京:高等教育出版社.2001

[3] 李瀚蓀.簡明電路分析基礎[M].北京:高等教育出版社.2002

[4] 李剛,林凌.電路學習與分析實例解析[M].北京:電子工業出版社.2008

[5] 李瀚蓀,吳錫龍.簡明電路分析基礎教學指導書[M].北京:高等教育出版社.2003

[6] 陳洪亮,張峰,田社平.電路基礎[M].北京:高等教育出版社.2007

Miller Theorem and Its Application

TIAN She-ping,CHEN Hong-liang

(Schoolo f E lectrica l and E lectronic Eng.,Shanghai Jiao Tong Univ.,Shangha i 200240,China)

Miller theorem has extensive app lication on circuit analysis and design.In consideration of present circuit teaching,the descrip tion and proo f of M iller theorem are discussed and app lication examp les about M iller theorem are introduced.Teaching suggestions are also given.M iller theorem has summ arized the circuits'law and can be app lied to analyzed circuits effectively.It is helpful for deepening students'understanding of circuits,enhancing ability of research and interests of learning.The discussion is helpfu l for the teaching of circuit.

miller theorem;circuit teaching;circuit analysis

TM 13

A

1008-0686(2011)02-0029-03

2010-09-04;

2010-11-30

田社平(1967-),男,博士,副教授,主要從事電路理論和動態檢測技術的教學和科研工作,E-mail:sptian@sjtu.edu.cn