論電磁慣性

梁昌洪,陳 曦

(西安電子科技大學天線與微波技術國防重點實驗室,陜西西安 710071）

論電磁慣性

梁昌洪,陳 曦

(西安電子科技大學天線與微波技術國防重點實驗室,陜西西安 710071）

偉大的物理學家牛頓首先提出了力學慣性定律:“每個物體將繼續保持其靜止或沿一直線做勻速運動狀態,除非有力加于其上迫使它改變它改變這種狀態。”而本文則在電磁領域提出相應的電磁慣性——每個電磁波都傾向于保持球三維或圓二維狀態向外傳播,除非有外加源或邊界迫使它改變這種狀態。文中,還把這一思想進一步擴展為電位φ和電荷σ的靜電慣性。

力學慣性;電磁慣性;靜電慣性;天線;最小方向性

0 引言

本文是電磁理論教學札記之十四。

在物理發展史上,電磁波的預言和發現無論如何是一件震驚世界的大事,其中天才的M axwell和伺后的Hertz起到了關鍵作用。

眾所周知,在M axwell之前,電磁領域已總結出Amber(1825)定律和Faraday(1831)定律,如式(1)和式(2)所示。

然而,在包含電容C的電路中出現了矛盾(即在頻域情況下,外電路存在電流,而電容C內部卻不存在電流)。經過反復推敲和思考,M axwell引入了位移電流:

從而解決了上述難題。這種情況下,上述三式可以變成

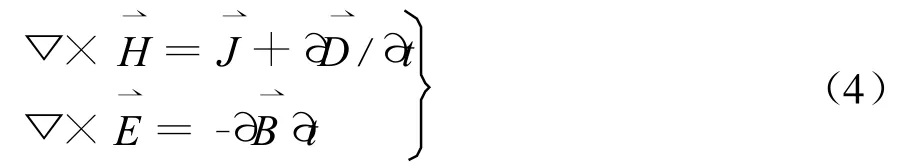
利用上式,可并在真正意義上完成了電和磁雙向的相互轉化 ——電場的時間變化(/ t)可以轉化為磁場的空間變化( ×);另一方面,磁場的時間變化(/ t)可轉化為電場的空間變化( ×)。正是這種和諧的雙向變化構成了電磁波出現的關鍵原因。

Maxwell還導出了電磁波的波動方程。對于最簡單的一維情況,有

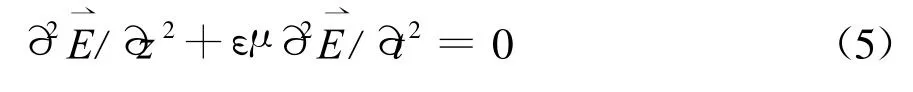
而波的速度正是光速c,即

Maxwell的預言通過Hertz的實驗,把這一事件推向了高潮,從而奠定了現代通信最重要的基礎。Hertz在1888年的論著《論電磁作用傳播的有限速度》和《論電磁輻射》,讓電磁波真正走到人類舞臺的前面,如圖1所示[1]。

圖1 Hertz實驗圖

所有這些都使M axwell電磁理論獲得了極大的成功,他實現了兩大綜合:光和電磁的統一;動場和靜場的統一。如圖2和圖3所示[2]。由此揭開了深入研究電磁波的序幕。

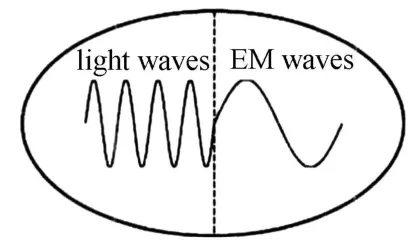
圖2 光和電磁的統一

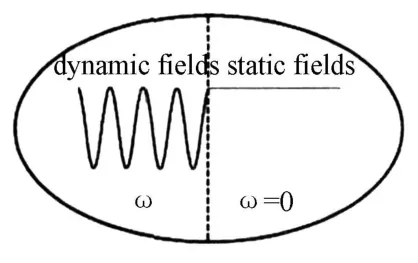
圖3 動場和靜場統一

1 電磁慣性

很少有人注意到:電磁波還具備一個重要的特性,即電磁慣性。廣義地說,電磁慣性包括動場的波慣性和靜場的位慣性與荷慣性。所謂慣性,指的是在完全沒有約束條件下事物的本質特性。

偉大的物理學牛頓最早揭示:每個物體將繼續保持其靜止或沿直線作勻速運動狀態,除非有力加于其上迫使它改變這種狀態[3]。

上述特性可稱之為力學慣性,也即牛頓第一定律。這時約束即力F ,在不變約束時事物的本質狀態即勻速直線運動或靜止。

與此對應,電磁慣性的原理首先是由Huygens提出的,它深刻揭示了波的形成和波的本質。他指出:“在一已知波前上的所有點,都可以看作產生次級球面波的子波源,它們仍以在該媒質中的波速向前傳播,其包絡形成新的波前。”如圖4所示。

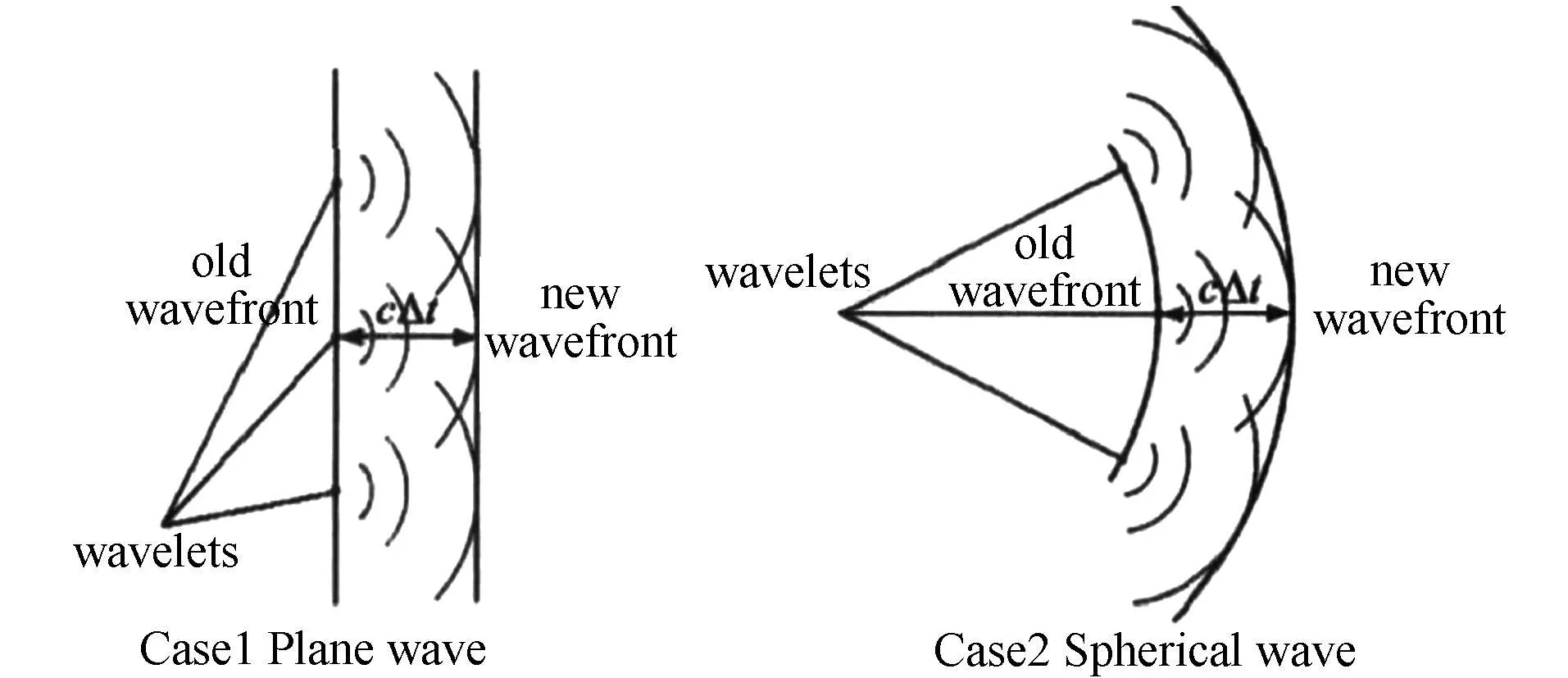
圖4 Huygens原理

十分明顯Huygens原理有兩點重要思想:

(1)子波思想——在波動的每一點,都可等效一獨立的理想源,它為進一步傳播波創造條件。

(2)球面波思想——每一子波都向外發出圓二維或球三維面波,可以認為球面波是波的無約束自由態(Free State)。

本文比較牛頓力學慣性,提出電磁慣性——“每個電磁波都傾向于保持球(三維)或圓(二維)狀態向外傳播,除非有外加源或邊界迫使它改變這種狀態。”完全可以這樣說,電磁約束即外源或邊界,而球和圓正是波的無約束自由態。

2 靜電慣性

如前所述,Maxwell已經把動場與靜場統一了起來。后者僅僅是不隨時間變化,那么,當動場具有電磁慣性的特性,靜電場中如何體現慣性呢?

我們深入研究后可明確指出:靜物依然具有靜電慣性。它可反映在兩個方面:電位φ分布慣性和電荷σ分布慣性。

2.1 電位φ分布慣性

十分巧合,我們是從一個典型實例中偶然發現這一重要特性的[1]。眾所周知,在電場中,導體邊界是一等位面。問題的研究是由正方形同軸線引入的。根據圖5的邊界條件,很易想到電位的試探函數也是圖示的正方形。但是出人意料的是采用這一思路算出的電容C和特性阻抗Z0與精確值相差較大。

上述矛盾給我們提供了深入思考的機會。最后總結出靜電位 φ分布慣性原理:“在靜電場中,一旦離開導體邊界的電位φ,它總有構成圓或球的傾向 。”

值得指出在某些情況下,因邊界所限它也盡可能地在橢圓或橢球之間游移,力爭獲得本身的自由。

圓或球狀靜電位φ分布是事物無約束的自由狀態,如圖6所示。數值計算完全證實了這一點[1]。

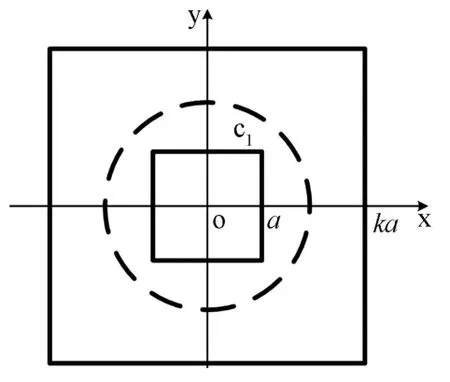
圖6 靜電慣性

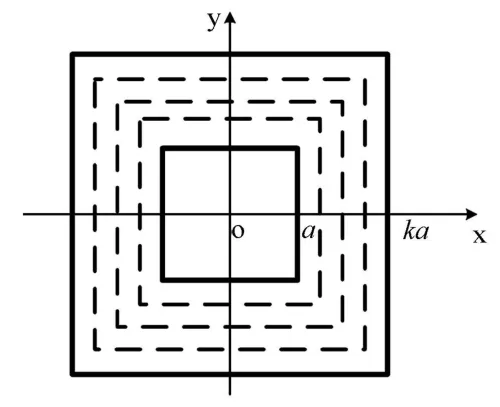
圖5 電位φ試探函數(k>1)

2.2 靜電荷σ分布慣性

在靜電場中,與位φ對應的物理量是電荷密度σ。作為一般形狀導體盤的電荷分布也有上述特點,圖7給出的實例表明電荷σ分布也存在圓的傾向。

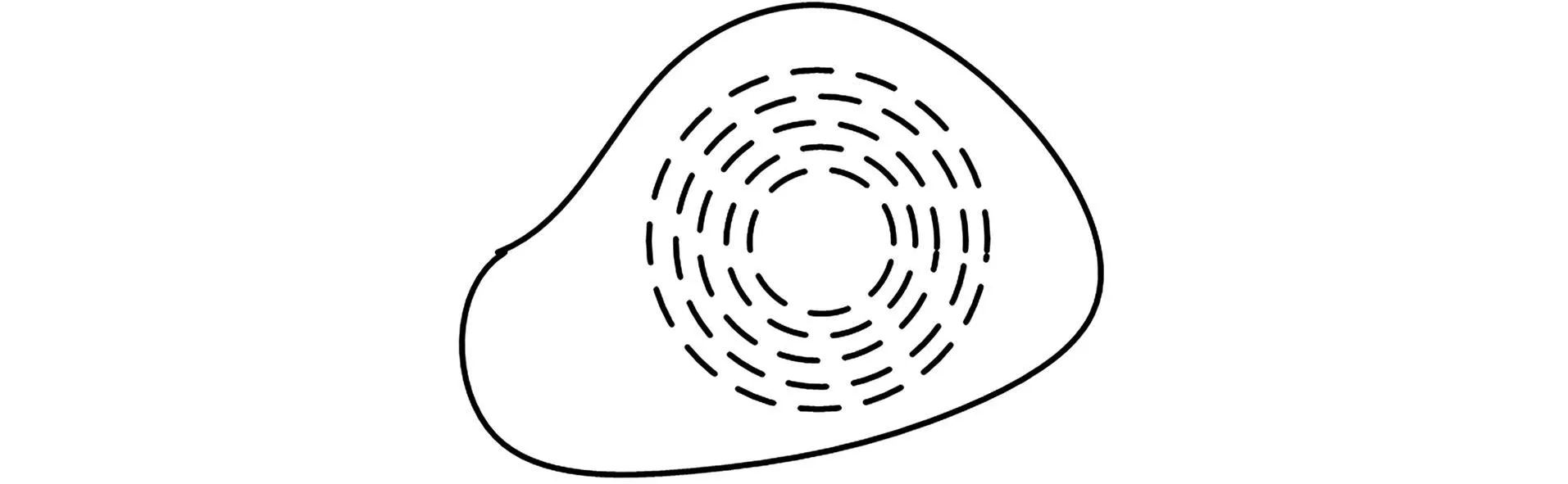
圖7 任意導體盤上電荷σ也存在圓的傾向

我們可以總結出靜電荷σ分布慣性原理:“在靜電場導體上的電荷σ分布,總有構成圓的傾向。”

3 Green函數與靜電慣性

在電磁理論中,G reen函數是一類廣義位,如圖8所示。

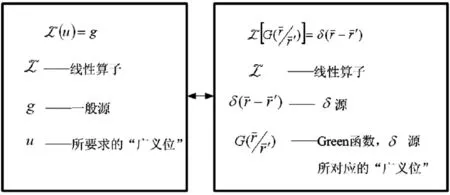
圖8 G reen函數和廣義位引入

十分清楚,δ函數可看作子波源或子源,而G則是子波。由表1清楚看出動場電磁慣性向靜場電磁慣性轉化的具體過程。

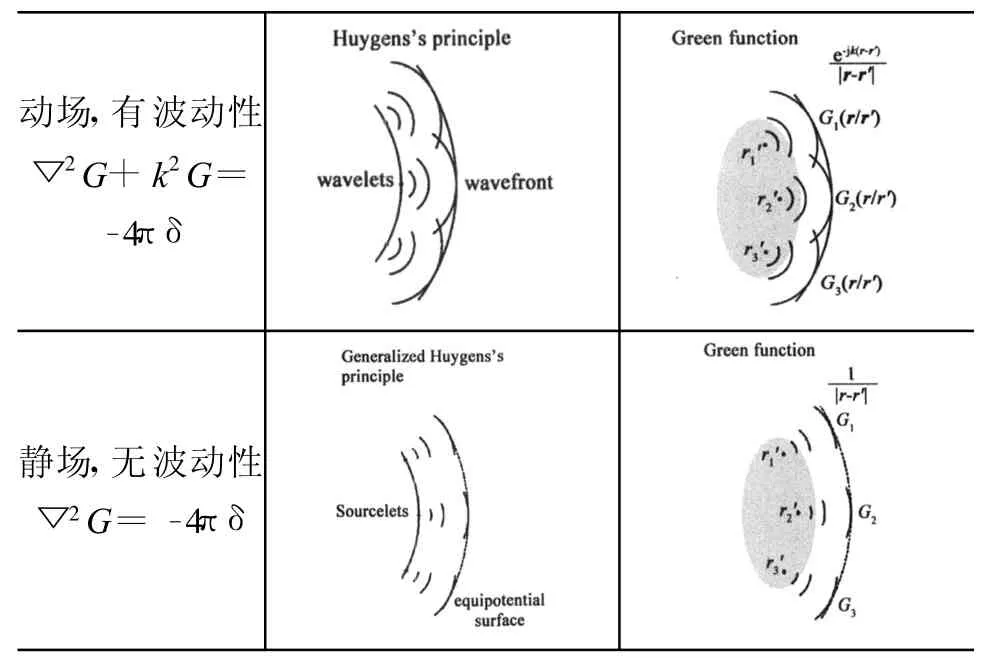
表1 動場電磁慣性和靜物電磁慣性

4 天線元無法構成理想子波源

在上面討論中,電磁慣性概念中還有一個要點:即各向同性不僅表示球面波,而且應該是均勻球面波,也就是各個方向傳播的振幅相等。這一點在Green 函數中即體現這種思想。

然而,實際上我們所遇到的則完全是另一種情景:即任何天線都無法構成向各個方向均勻輻射的理想子波源,問題的樞紐在于極化。

不論是如圖9所示的電荷偶極子或電流小圓環,其本身分布都不是各向同性的。它們所對應的方向性系數最小為1.5,即

圖9 存在極化分布的天線元

我們完全可以猜測:這可能也是任何電磁輻射的最小方向性。

5 結語

牛頓給人類帶來的不僅是萬有引力定律和 F=m a。他從力學的觀點出發,深刻揭示了物質的一個最重要概念——電磁慣性:“在沒有外力的條件下,物體保持其靜止或勻速運動狀態。”它在本質上說明了慣性表示物體力學的自由態,也是物體的一個本質屬性。

本文提出的電磁慣性,可以說是事物在電磁領域的對應特性。它可以表述為:“在沒有外源的條件下,每個波都傾向于以球(三維)或圓(二維)狀態向外傳播,除非有外加源或邊界迫使它改變這種狀態。”

我們十分有興趣地指出:力學慣性——勻速直線運動實際上有可能無限逼近;與之相反,電磁慣性——各向同性的球面波是實際天線(外加源)輻射無法達到的。這一對比的哲學意義非常值得進一步探索。

本文又進一步提出靜電慣性——“在靜電物中,一旦離開導體邊界的電位φ分布,它總有構成圓或球的傾向”和“在靜電物中,導體上電荷σ分布,總有構成圓的傾向。”

它們清楚表明不論是波還是非波狀態,都有趨向球或圓的自由態傾向,這就是本文需聚焦的主題——廣義電磁慣性。

[1] 錢長炎,在物理學與哲學之間——赫茲的物理成就及物理思想[M].廣州:中山大學出版社,2006

[2] 梁昌洪,廣義惠更斯原理[J].北京:電子學報,Vol.36,No.12,pp.2439-2444,Dec.2008

[3] 梁昌洪,話說對稱[M].北京:科學出版社,2010

Research of Electromagnetic Inertia

LIANG Chang-hong,CHEN Xi

(State Key Lab.o f Antennasand M icrowave Techno logy,X id ian University,X ian,710071,China)

I.New ton,a great physical scientist,first proposed the law of force inertia:a body will rem ain in its state of rest or of uniform motion in a straight line untile was acted upon by an ex ternal force to change the state.This paper presents the electromagnetic inertia that a electromagnetic wave w ill spreed with the tendency ofa sphere in 3-dimensionalor a circle in 2-dimensionalunless external source or boundary was acted to change the state.This idea is ex tended to electrostatic field o f electric potentialφand electric chargeσ.

force inertia;electromagnetic inertia;electrostatic inertia;antenna;minimum directivity

TM 15

A

1008-0686(2011)02-0001-04

2010-12-28;

2011-02-21 基金項目:教育部《創新教學團隊》資助

梁昌洪(1943-),男,教授。主要從事電磁場數值分析、電磁輻射與散射、電磁兼容、電磁網絡等領域的研究工作;

陳 曦(1982-),女,博士研究生,研究方向為電磁場理論輔導和電磁新材料及其在天線上的應用研究,E-mail:chenxi8206@163.com