微分方程模型在種群問題中的應用

代麗麗，王 煜

(通化師范學院 數學系，吉林 通化 134002)

全球生態環境的日益惡化越來越引起人們對種群生長和種群對其生存空間依賴性的重視.許多生態學者和數學工作者對這方面的問題進行了深入研究，并得到了一些有意義的研究成果.眾所周知，人類生存環境的改善能造福人類，但也會產生一些負面的影響，這其中就包括對人類生存環境的破壞.人類及其它生物種群生存環境的生態平衡與社會的可持續發展關系重大，如何使人類在享受大自然，利用大自然的同時，又能保護大自然，這是人們一直關心的問題.并由此而產生了生物學的研究分支.生物數學是生命科學與數學之間的邊緣學科，它是應用數學理論與計算機技術研究生命科學中數量性質、空間結構形式，分析復雜的生物系統的內在特性，揭示在大量生物實驗數據中所隱含的生物信息.

回顧生物數學發展的近百年歷史，我們清楚的看到，對生物數學的研究越來越受到人們的重視，且在各個分支上的理論研究也在不斷地成熟與完善.就不同時期的生物種群數學模型而言，早在1798年，英國的經濟學家和人口學家Malthus就提出了描述種群發展過程的動態數學模型，也稱為Malthus模型[1].

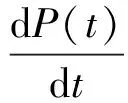
1838年，比利時社會學家P.F.Verhulst改進了Malthus模型，考慮到環境容量又提出了Logistic模型[2]

其中常數λ和K分別稱作種群的內在增長率和環境容量.

容易看到，由于這兩個模型都沒有考慮到年齡分布等因素，因而對于壽命較長，世代重疊的物種(例如人口)會產生較大的偏差，而其種群的年齡結構往往也是人們十分關心的信息.為此，又建立了與年齡相關的時變種群數學模型.

1 與年齡相關的線性種群數學模型

F.R.Sharpe和A.J.Lotka在1911年以及A.G.M-kendrick在1926年提出與年齡相關的連續模型，并由H.Von Foerster進行改進，得到了下面的數學模型(P1)[3].

2 與年齡相關的非線性種群數學模型

從種群發展過程的實際出發，我們不容忽視種群擁擠和生存環境對種群發展過程的影響，這就導致人們又建立了如下的與年齡相關的非線性種群數學模型(P2)[4]:

對于系統(P2)，人們從不同的側面對它進行了研究，得到了很多重要而有意義的研究結果.

1985年，G.F.Webb[5]總結了前人有關解的存在性、穩定性等工作，并用半群的方法進一步對系統(P3)在定常情形的解的存在性和穩定性做了研究，得出了系統解的穩定性結果.

1999年，陳任昭和李健全[6]對非線性時變種群系統(P3)的一般情形解的存在唯一性給出了證明，把定常情形的結果推廣到時變情形.

3 與年齡相關的線性種群系統的邊界控制問題

對于種群系統(P1)的邊界控制問題，1999年，曹春玲，陳任昭[7]討論了與年齡相關的時變種群系統(P3):

的邊界控制問題，證明了最優控制的存在性，得到了控制為最優的必要條件，給出了由積分-偏微分方程和變分不等式組成的最優性組.

2000年，徐文兵，陳任昭[8]討論了時變種群系統(P4)：

具最終狀態觀測的最優邊界控制問題，證明了系統解的存在唯一性，得到了最優邊界控制的存在性及控制為最優的必要條件.

4 具年齡分布和加權的種群數學模型

考慮到不同年齡的種群個體對種群發展過程的實際影響，人們又相繼研究了半線性種群系統和加權種群系統的最優控制問題.1999年，Barbu V.和Iannelli M.[9]討論了生育率和死亡率均依賴于種群加權總規模S(t)的半線性種群模型(P5)：

并針對于性能指標泛函為

的情形，證明了系統(P5)最優控制的存在性.

2006年，何澤榮，朱廣田[10]針對于生育率和死亡率均依賴于個體年齡的情形，提出了加權總規模的數學模型(P6):

其中Q=(0，A)×(0，T)，固定常數A，T分別表示個體最高壽命和控制周期.狀態變量p(a，t)表示t時刻年齡為a的個體數量，控制函數u代表收獲努力度.S(t)表示t時刻種群的加權總量，ω為權函數.β，μ表示出生率和死亡率，它們都與S有關，意味著不同年齡的個體對種群的演化具有不同的影響.P0為初始年齡分布.借助不動點原理確立了系統的適定性，應用極大化序列法和緊性證明了最優收獲控制的存在性，利用法錐和共軛系統技巧導出了最優性條件，推廣了一些文獻的工作.

2007年，葉山西，趙春[11]研究了具年齡分布和加權的非線性種群系統(P7):

的最優分布控制問題，應用Ekeland's變分原理證明了最優分布控制的存在性，并用法錐和共軛系統技巧導出了最優性條件.

參考文獻：

[1]Malthus T R.An Essay on the principle of population as it Affects the Future Improement of Society，with Rwmarks on the Speculations of M Condorct and other writer[M].London:J Johnson，798.

[2]Verhulst P F.Notice Sur la Loi Que Population Unit Son Accroissement[J].Correspones Mathematiques et physiques，1838，10:113-121.

[3]Foerster H Von.Some Remarks on Changing Population in the Kinetics of Celluar Proliferation[M].New York:Grune and Stratton，1959.

[4]Gurtin M E，MaCamy R C and Hoppensteadt F.Nonlinear Age-dependent Population Dynamics.Arch[J].Rat.Mech.Anal，1974，54:281-300.

[5]Webb G F.Theory of Nonlinear Age-dependent Population Dynamics[J].Pure and Applied Mathematics，New York:Dekker，1985.

[6]陳任昭，李健全.非線性時變種群系統解的存在唯一性[J].數學物理學報，2003，23A(2):1-17.

[7]曹春玲，陳任昭.時變種群系統的最優邊界控制[J].東北師范大學學報，1999(4).

[8]Barbu V and Iannelli M.Optimal Control of Population Dynamics[J].J.Opti.Theo.Appl，1999，102(1):1-14.

[9]徐文兵，陳任昭.時變種群系統最終狀態觀測及邊界控制[J].東北師范大學學報，2000，32(1).

[10]何澤榮，朱廣田.基于年齡與分布和加權總規模的種群系統的最優收獲控制[J].數學進展，2006，35(3):315-324.

[11]葉山西，趙春.一類具有年齡分布和加權的種群系統的最優控制[J].應用數學，2007，20(3).