雙弓作用下錨段關節處弓網耦合系統受流分析
王 暉,張忠林,畢繼紅
(天津大學建筑工程學院,天津 300072)
高速列車運行過程中,機車通過受電弓從接觸線上獲取電能,在高速情況下穩定受流是列車正常運行的保證,為此弓網關系也就成為研究設計人員關注的焦點。研究表明,雙弓機車可以有效的降低離線率,提高受流質量[1~4]。特殊情況下,例如在冬天的時候,接觸網上結了一層薄冰,這時升雙弓,前弓把冰給刮掉,后弓能夠很好的受流。研究還發現,錨段關節處更易出現受流不穩定的問題[5],研究關節處的受流情況有應用的價值。
本文以sss400+受電弓、CTMH150-2接觸線為原型,基于大型有限元軟件ANSYS建立了2個連續錨段的雙弓弓網耦合系統的有限元模型。采用單一變量的方法,研究了跨距、列車運行速度、弓頭質量、接觸線張力、雙弓間距等參數對雙弓弓網耦合系統在錨段關節處動態受流特性的影響。以期為鐵路的提速和舊線路改造提供有價值的參考。
1 仿真模型和評價標準
1.1 接觸網模型
接觸網示意如圖1所示,包括承力索、接觸線、彈性吊索、吊弦、上下線夾及一些附屬結構(用集中質量代替)。表1所示為某線接觸網參數。接觸線、承力索及彈性吊索采用Beam4單元模擬;吊弦采用Combin39單元模擬;上下線夾及集中質量均采用Mass21單元模擬。
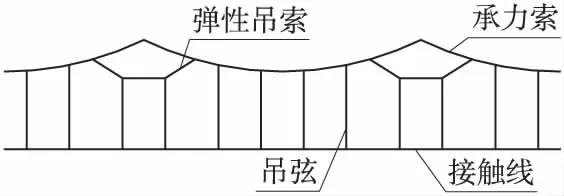
圖1 接觸網示意
1.2 受電弓模型
受電弓以sss400+為原型,計算模型如圖2所示。采用三元集中質量模型[6~8],質量塊采用Mass21單元模擬,彈簧采用Combin14單元模擬。表2所示為某線受電弓參數,圖中Mi,Ki,Ci,fi分別為受電弓模型中的質量,剛度,阻尼及干摩擦;Fk為受電弓的靜態抬升力,189 N。雙弓間距201 m。
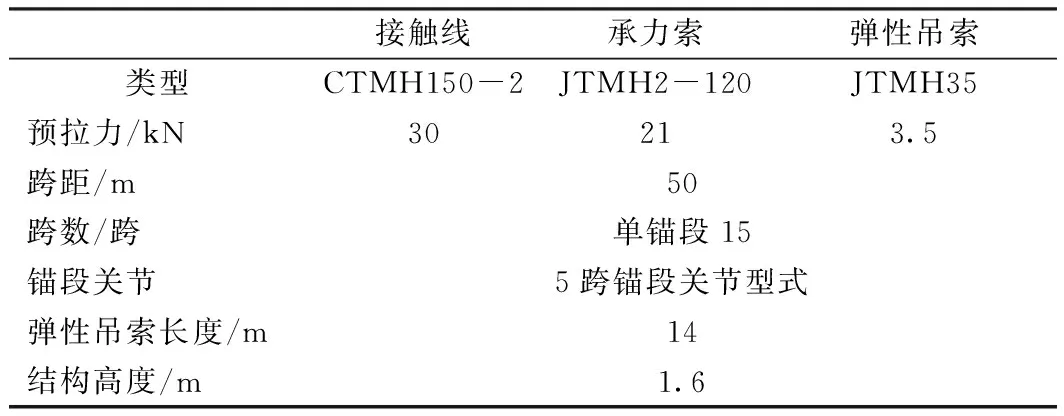
表1 接觸網參數
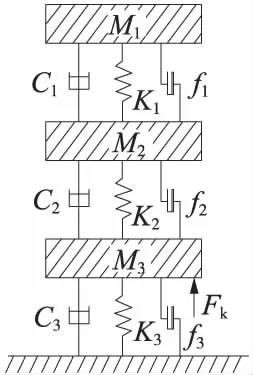
圖2 受電弓計算模型

質量/kg阻尼/(Ns/m)剛度/(N/m)干摩擦力/NM1M2M3C1C2C3K1K2K3f1f2f36.056.4140064.9581313600038.58.5
1.3 弓網耦合
受電弓與接觸網之間的耦合是通過設置“接觸對”的方式來實現的[5]。接觸線作為目標單元采用Targe169單元模擬,受電弓作為接觸單元采用Conta175單元模擬,形成接觸對,建立起弓網耦合系統;在建立錨段關節時,將2個錨段的接觸線分別設置成目標單元,弓頭分別與第1錨段、第2錨段建立接觸對,以實現受電弓運行時從第1錨段向第2錨段的過渡。
1.4 評價標準
以大型有限元計算軟件ANSYS為基礎,利用時間-歷程后處理器,提取動態接觸力、弓頭位移以及接觸線位移的數據。參照歐洲聯盟和日本制定的受流質量評價標準[9],以接觸力的最值、幅值和標準差,弓頭位移的最大值、標準差和接觸線位移的最大值、標準差來評價整個系統的受流質量。
2 仿真結果及分析
提取中間錨段處的數據,采用單一變量法,分析各因素對受流質量的影響。
2.1 列車運行速度的影響
不同列車速度下,接觸力和位移變化如圖3、圖4所示。

圖3 接觸力隨列車速度的變化
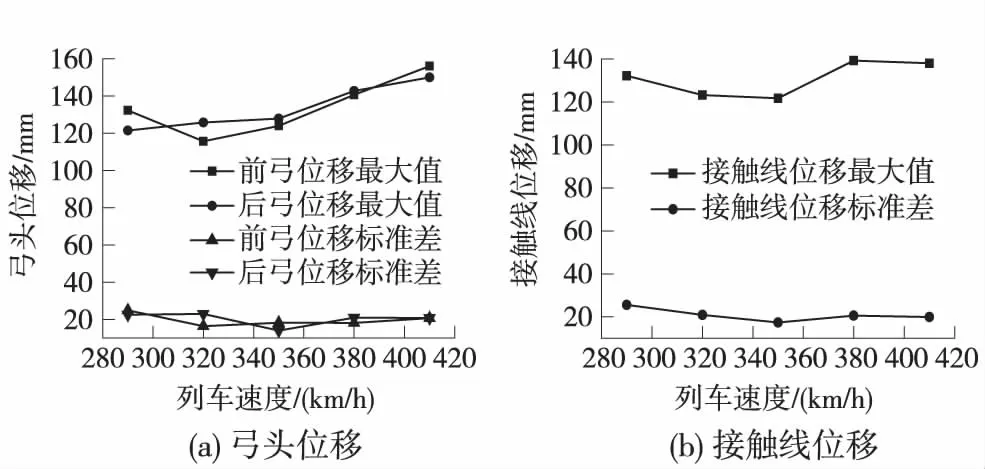
圖4 位移隨列車速度的變化
隨著速度的增長,前弓和后弓接觸力最小值變小、幅值變大,后弓接觸力標準差增大,說明受流質量逐漸變差;同時隨速度增大,后弓弓頭位移最大值也逐漸增大;速度增大到380 km/h時,后弓出現離線現象,可見在高速時,后弓受流質量對速度的變化更加敏感,但前弓受流質量仍優于后弓。
2.2 雙弓間距的影響
不同雙弓間距下,接觸力和位移的變化如圖5、圖6所示。
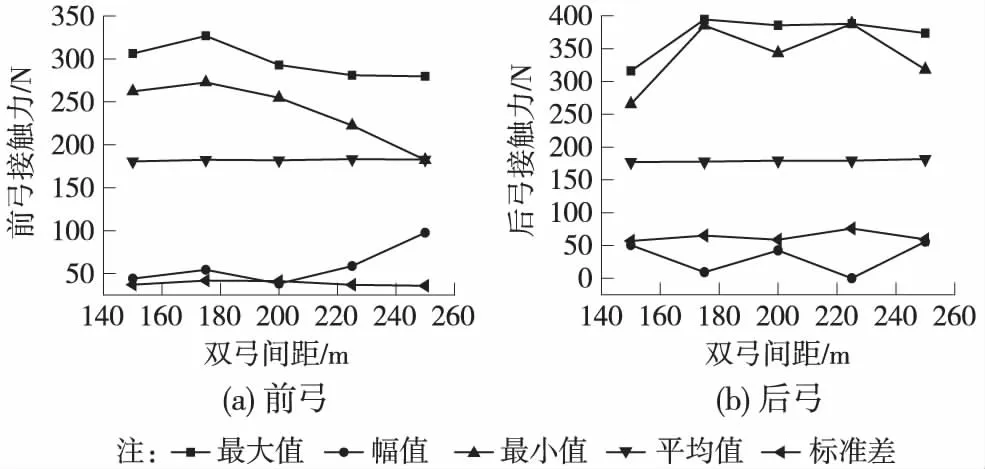
圖5 接觸力隨雙弓間距變化
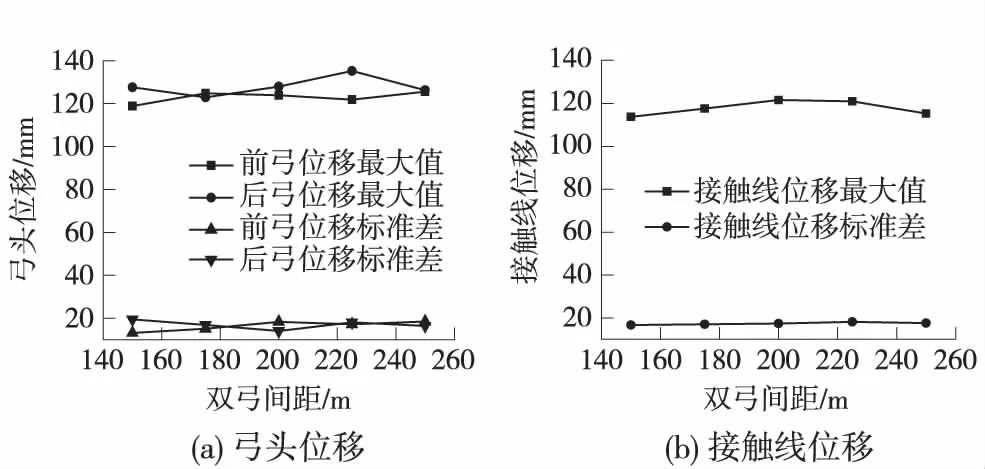
圖6 位移隨雙弓間距變化
當雙弓間距為150、201 m和250 m時,后弓接觸力最小值較大,幅值較小,標準差較小,受流質量較好。即當雙弓間距為跨距的整數倍加半跨時,后弓受流質量最差。對于前弓,這種規律表現不明顯,但前弓受流質量仍優于后弓。弓頭位移和接觸線位移隨雙弓間距的改變變化不大。
2.3 接觸線張力的影響
接觸線張力選取不同數值時,接觸力、位移隨接觸線張力的變化如圖7、圖8所示。
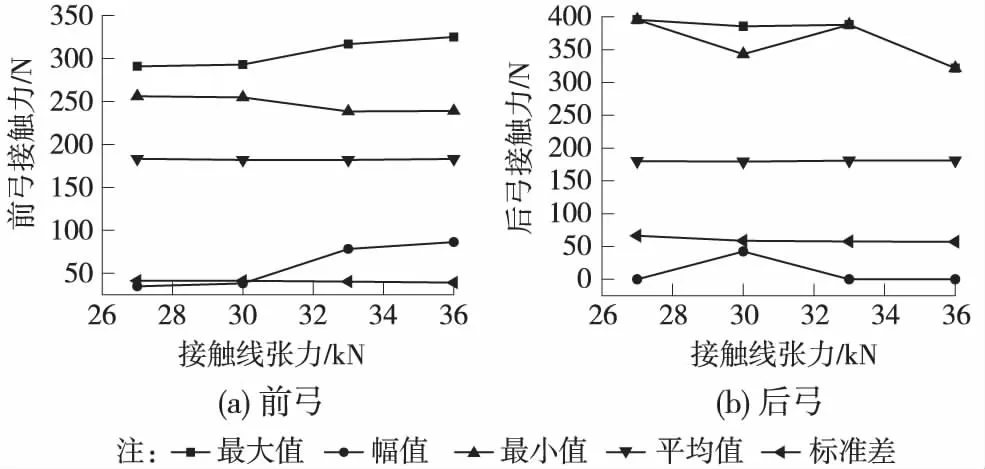
圖7 接觸力隨接觸線張力的變化
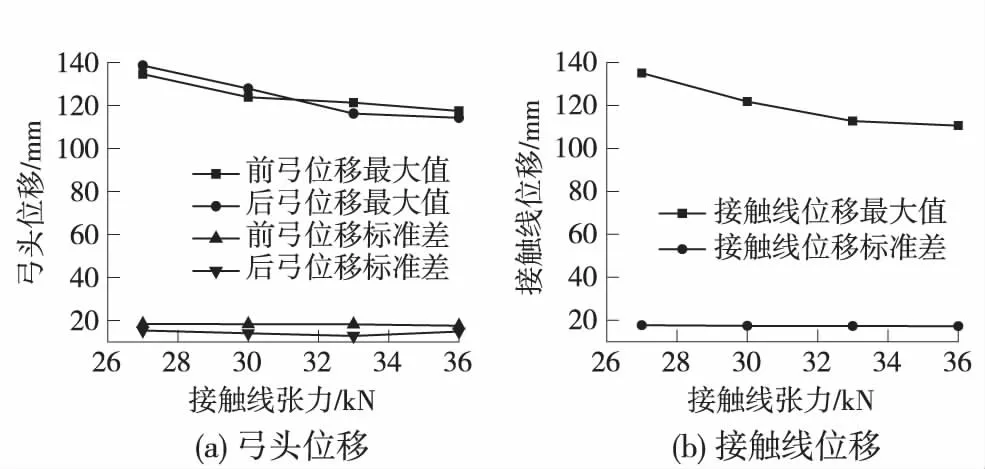
圖8 位移隨接觸線張力的變化
隨著接觸線張力的增大,前弓接觸力的最大值、最小值逐漸增大,接觸力標準差亦有變小的趨勢,說明前弓受流質量逐漸提高。前弓弓頭和接觸線位移的最大值和標準差都隨著接觸線張力的增大逐漸減小,這是因為接觸線張力越大,整個接觸網的剛度就越大,這對前弓受流有利。后弓接觸力標準差也隨接觸線張力的增大而減小,說明接觸線張力增大同樣對后弓受流有利,但是后弓的受流狀態受前弓的影響,受流質量較差。
2.4 弓頭質量的影響
不同受電弓弓頭質量下,接觸力、位移隨弓頭質量變化如圖9、圖10所示。
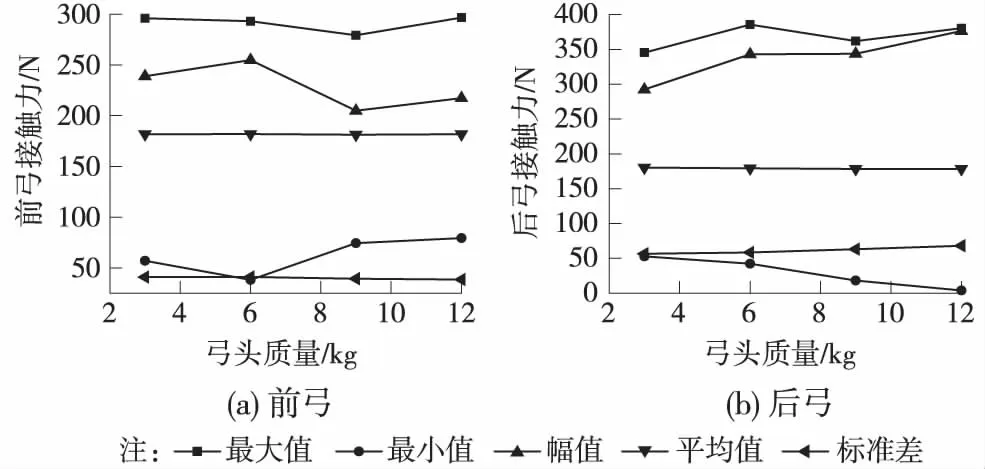
圖9 接觸力隨弓頭質量變化
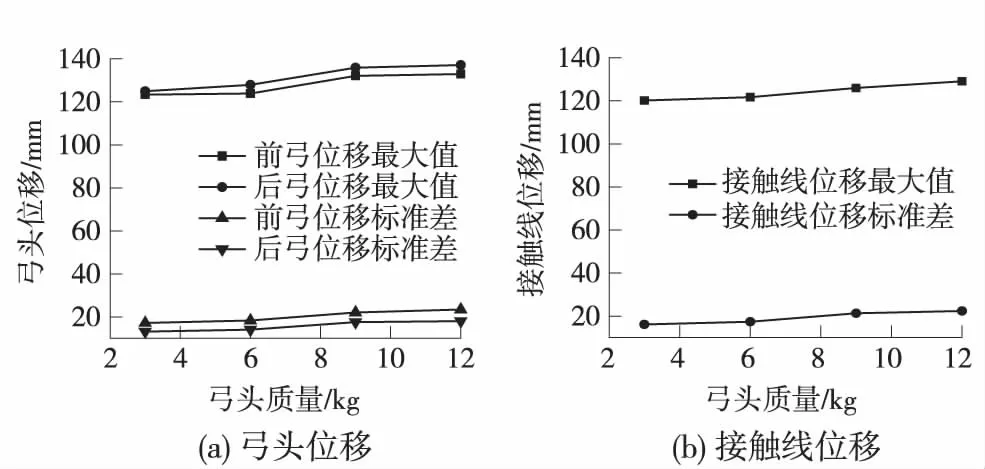
圖10 位移隨弓頭質量變化
隨著弓頭質量的增大,后弓接觸力最小值減小,幅值增大,平均值減小,標準差變大,后弓受流質量變差。弓頭質量的增加對前弓接觸力的影響并不顯著。隨著弓頭質量的增大,前弓、后弓和接觸線位移的變化規律一致,都為位移最大值增大,標準差增大,受流質量有變差的趨勢。總體而言,隨著弓頭質量的增加,受流質量變差。
2.5 跨距的影響
不同跨距下,接觸力、位移隨跨距變化如圖11、圖12所示。
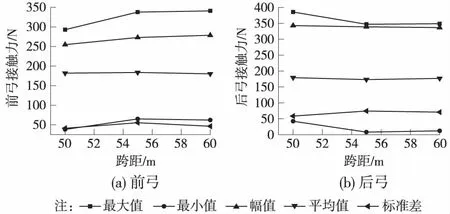
圖11 接觸力隨跨距變化
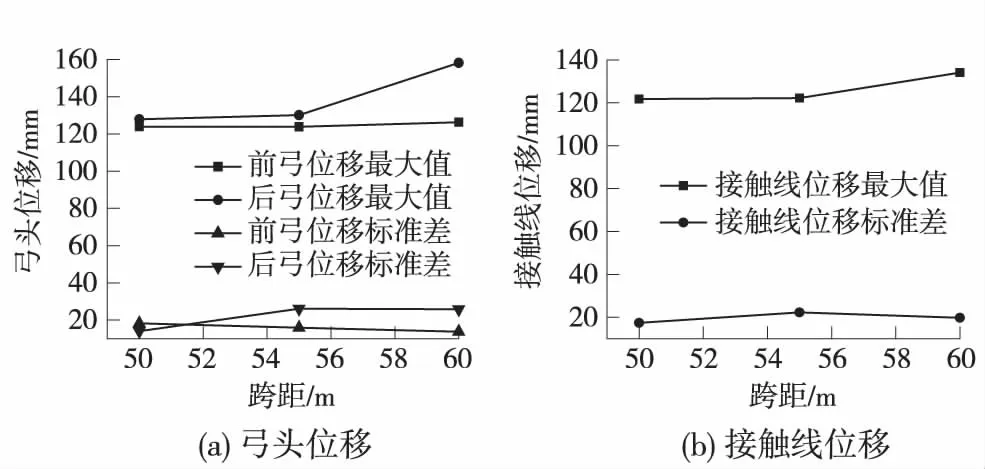
圖12 位移隨弓頭質量變化
跨距改變對弓頭接觸力的影響不大。但在50 m時,前弓接觸力最大值最小,幅值最小,標準差最小,后弓接觸力最小值最大,標準差最小,受流質量最好。位移方面,在50 m時,后弓和接觸線位移的最大值最小、標準差最小,受流較好。
這是因為跨距增大時整個接觸網的彈性增大,對受流不利。高速鐵路更適合用小跨距,但也應考慮造價的因素。
3 結論
在列車高速運行情況下,錨段關節的受流情況變得更加復雜。速度提高,受流質量變差,且后弓受流質量對速度的變化更加敏感;當雙弓間距為跨距的整數倍加半跨時,后弓受流質量最差,但對于前弓這一規律不再明顯;提高接觸線的張力、減小弓頭質量、減小跨距可以提高錨段關節處的受流質量。受前弓在接觸線上運動產生振動波的影響,錨段處后弓的受流質量仍比前弓差。
[1] 于萬聚.高速接觸網的受流穩定分析[J].西鐵科技,1996(2):38-44.
[2] 于 滌.高速接觸網受流的理論分析[J].鐵道學報,1998,20(5):58-64.
[3] Gao X. Contact wire zigzag value detection in the electrified railway, Proceedings of SPIE-The International Society for Optical Engineering, 2001,4285:60-68.
[4] 衛仙鳳.雙弓作用下弓網耦合系統的動態模擬分析[D].天津:天津大學,2010.
[5] 孟令倩.柔性懸掛系統的參數化建模及錨段關節的受流分析[D].天津:天津大學,2010.
[6] 李 鵬.弓-網耦合系統的動態模擬及疲勞分析[D].天津:天津大學,2009.
[7] 李豐良,等.受電弓的力學分析示例[J].鐵道學報,2000,22(5):21-23.
[8] 李豐良,等.TSG3受電弓的歸算質量[J].鐵道學報,1998,20(2):55-58.
[9] 黃 維.高速接觸網懸掛參數標準與評價研究[D].成都:西南交通大學,2007.

