煙葉間可替代性的多元統計檢驗評價

杜 文,張其龍,易建華,黃振軍,任建新

湖南中煙工業有限責任公司技術中心,長沙市勞動中路426號 410007

按產地、品種和等級細分煙葉原料超過千種,配方人員需要進行大量的單料煙評吸和試制工作來維護卷煙產品內在質量的穩定。通過客觀檢測數據來評價不同煙葉間的可替代性對于卷煙產品設計具有重要的意義[1]。然而,目前我國煙草工業企業普遍使用的糖、氮、堿、氯等煙葉常規化學成分指標在煙葉內在質量評價中只能起到非常有限的參考作用[2-3]。因此,進行了本研究,旨在為卷煙產品葉組設計和配方打葉設計提供參考。

1 材料和方法

1.1 材料

2004年度片煙樣品,按產地、等級和品種不同取樣80類,每類均為工業企業作為同一種煙葉使用的原料。每類煙葉取樣12～60個,共取樣2482個,取自儲存了一年左右的湖南中煙工業有限責任公司的片煙倉庫。

M PA型近紅外光譜儀(德國B ruker公司),配積分球和旋轉樣品臺采樣附件;Cyc lotec 1093型旋風磨(瑞典Foss公司)。

1.2 方法

1.2.1 樣品常規化學指標的近紅外檢測

樣品于40℃下烘干,粉碎,過40目篩。用近紅外(N IR)光譜儀采集煙末樣品的漫反射近紅外光譜,掃描條件:分辨率8 cm-1,光譜范圍4000～9000 cm-1,重復掃描64次。用N IR模型預測煙末樣品的總糖、總氮、總堿、氯、纖維素、淀粉、多酚、灰份、醚提取物總量和總揮發堿。

1.2.2 煙葉集之間的可替代性評價

在超過30個樣本的類中隨機取15個樣品構成一類,共取30類450個樣品作外部檢驗集,編號V 1～V 30。剩余的2032個樣品作目標集,共80類,編號D1～D 80。編號序號x相同的外部檢驗集樣品Vx和目標集樣品Dx具有相同的產地、等級和品種屬性。

設某煙葉集X1有n1個樣本,某煙葉集X2有n2個樣本,每個樣本均有p個檢測指標,那么評價煙葉X1與X2之間是否可替代可用多元統計中的均值檢驗問題來表示:對于協方差不同的兩個多元正態分布,其均值差異檢驗被稱作Behrens-Fisher問題[4-5],在此問題中,若兩個多元正態分布X1,X2的樣本數n1,n2均大于數據維數p,可依據近似T2分布檢驗樣本均值所屬的總體均值(μ1,μ2)是否相同[6],即兩組樣本是否有顯著性差異:

對于假設H0:μ1-μ2=0,顯著性水平為α的拒絕臨界值c2可由F分布計算[7]:

式中:ν=

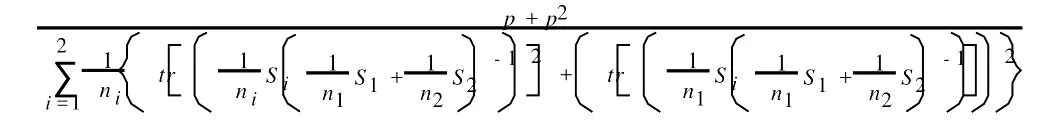
2 結果與討論

2.1 化學成分檢測值分布的正態性

進行多元近似T2檢驗的前提是多元變量要符合正態分布。因此,依據正態分布的特點對多個變量逐一進行正態分布檢驗[8]。即計算2482個樣本的10項化學成分指標的xj-zj數據,每100個樣本為一段,每項指標得到25對xj-zj數據,以總堿為例,x1為從小到大排列的第100個檢測值(0.89),z1為累積概率為(100的正態分布累積點(-1.75),依次計算,得到總堿檢測值的x-z關系圖(圖1)。計算每項化學成分檢測值x-z數據的線性相關系數,評價其分布的正態性,結果,總糖、總堿、總氮、淀粉、纖維素、多酚、灰份、揮發堿、氯、醚提取物總量的相關系數分別為0.9727,0.9806,0.9933,0.9936,0.9964,0.9981,0.9983,0.9939,0.9309,0.9904。自由度為25,顯著性水平α為0.05的線性相關檢驗臨界值為0.9591。由此可見,除氯以外,其他9項指標均超過該臨界值,即這9項指標可視作符合正態分布,可以進行多元近似T2檢驗。

2.2 化學成分檢測數據集的協方差等價性檢驗

若兩個多樣本多變量數據集中各變量符合正態分布,且兩個分布的協方差等價,則其均值向量是否有顯著性差異可用Hotelling’s T2檢驗來判斷[9]。由于煙葉化學成分的波動受農業、流通、工業等環節多種復雜因素的影響,各類煙葉的化學成分值分布有顯著的不同[10],不同數據集間協方差等價的條件不具備,故用Box’sM-test[7]檢驗樣本數分別為n1和n2的兩個p元數據集的協方差S1和S2是否等價,對于假設H0:Σ1=Σ2,統計量C符合卡方(χ2)分布:

圖1 煙葉總堿檢測值(x)-正態分布累積點(z)關系圖

給定顯著性水平α,拒絕H0的臨界值為:(α)。

用式(3)對80類煙葉中樣本數大于30的30個數據集的協方差進行兩兩配對檢驗,結果見圖2。由圖2可見,對于9項檢測指標p=9,檢驗臨界值(0.05)=61.6,大部分C值超出了該臨界值,表明各分布的協方差不能視作等價。

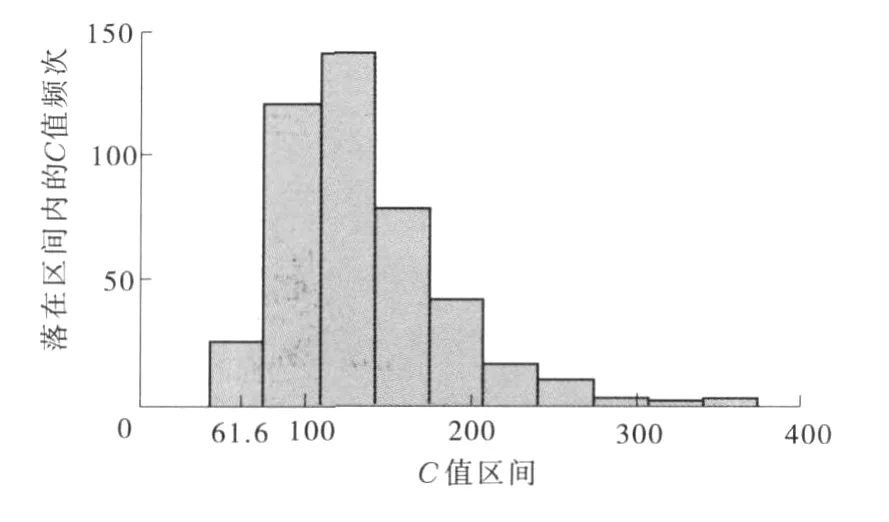
圖2 協方差等價性檢驗

對于協方差不等價的多元分布,需要用近似Hotelling’s T2檢驗判斷分布之間是否有顯著性差異[4]。

2.3 煙葉間的可替代性評價

用式(1)計算檢驗集V 1～V 30與目標集D 1～D 80之間的T2值,用式(2)計算其在顯著性水平α=0.01下的拒絕臨界值c2,以T2/c2值判斷兩煙葉數據集是否有顯著性差異,若T2/c2<1,則表明兩種煙葉無顯著性差異,即具有可替代性。計算結果見表1。表1數據顯示:①檢驗集30類煙葉(V 1～V 30)與目標集(D 1～D 30)的T2/c2<1,而與其他目標集的T2/c2>1,表明檢驗集30類煙葉都被正確地判斷為與其原來所屬的目標煙葉具有可替代性,并與其他目標煙葉不具有可替代性,本研究采用的煙葉替代性評價方法分辨性好;②T2/c2>1的結果,可以用來作為評價煙葉數據集相似性的度量,T2/c2值越小,煙葉間的相似性越高,替代使用的可行性越高。譬如,檢驗集V 22(瀏陽C2L)與目標集D 23(瀏陽C3F)間的T2/c2值為1.33,說明瀏陽C2L和瀏陽C3F較相似,相互替代使用有較高的可行性。

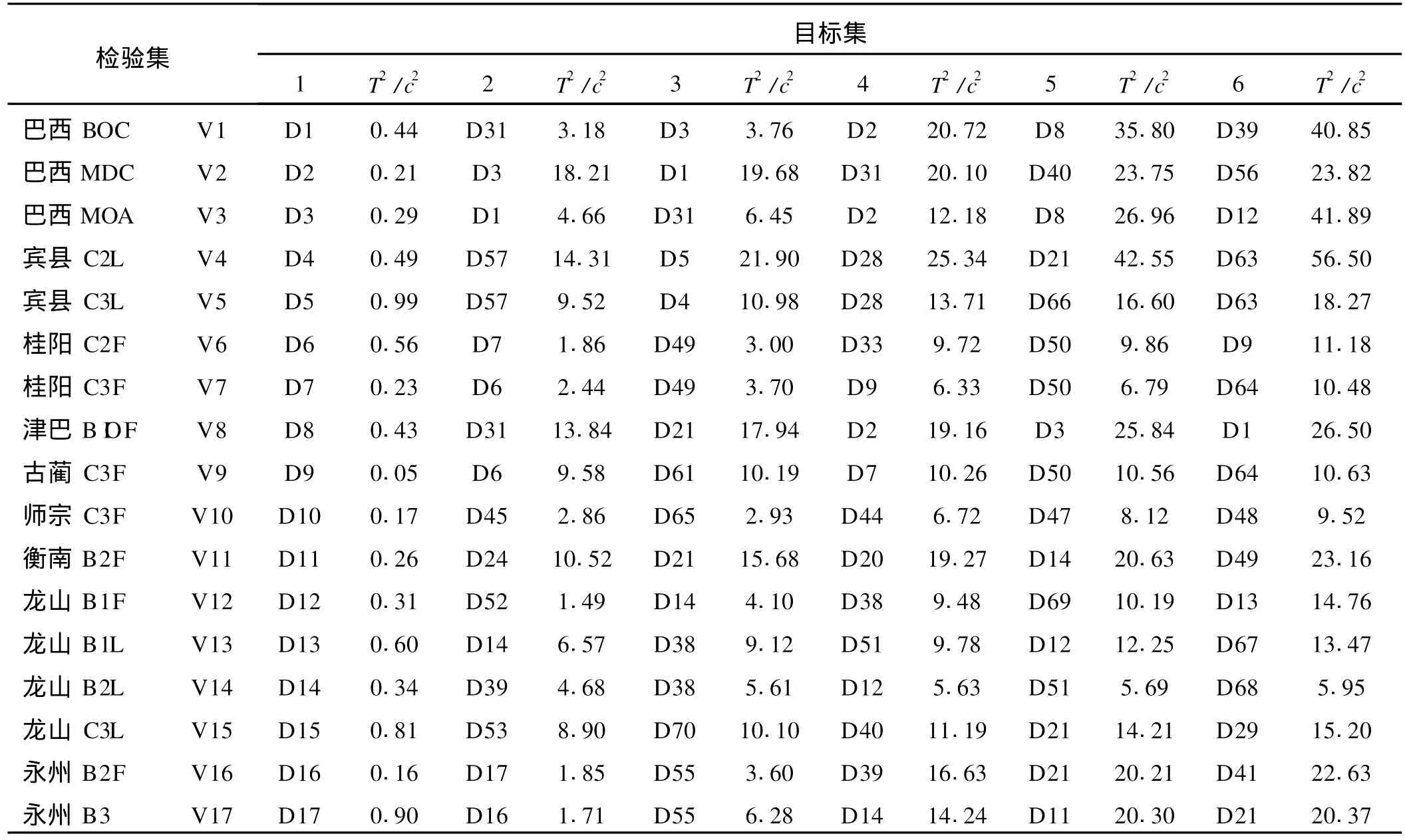
表1 檢驗集與目標集間的近似T2檢驗結果(T2/c2值從小到大排序前6位)①

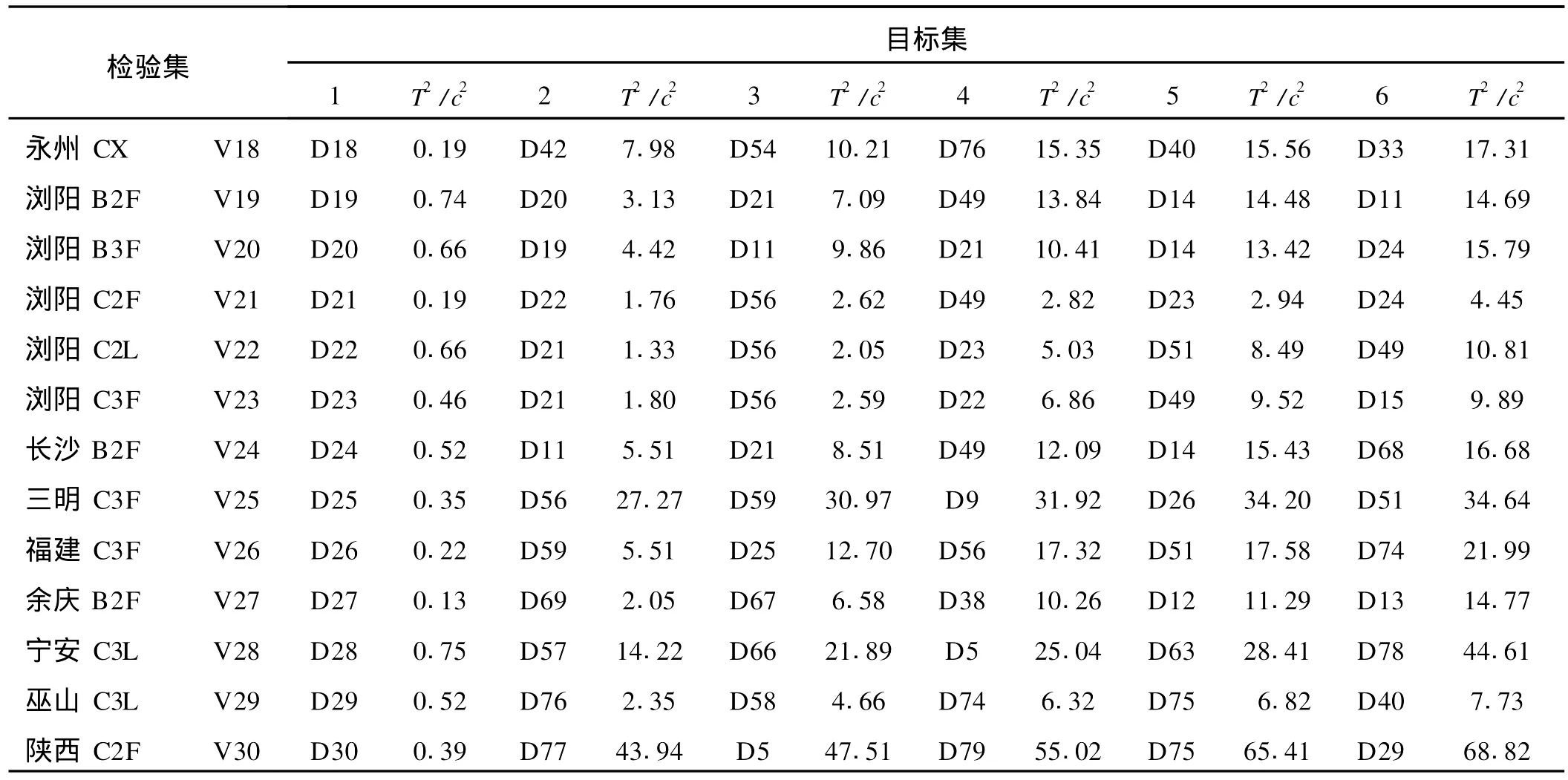
(續表1)

3 結論

用總糖、總堿、總氮、淀粉、纖維素、多酚、灰份、揮發堿和醚提取物總量9項化學成分指標通過多元均值檢驗評價煙葉間的可替代性具有較高的準確性,T2/c2值越小,相似性越高,T2/c2值可為相似煙葉的尋找提供有價值的線索。如果加入更多化學成分指標信息,煙葉可替代性判別的可靠性應會更高。

[1] Dale Hill.迎接挑戰——認識煙葉的質量和可用性[J].煙草科技,1997(1):34-36.

[2] 薛超群,尹啟生,王信民,等.烤煙煙葉香氣質量與其常規化學成分的相關性[J].煙草科技,2000(9):27-30.

[3] 朱尊權.煙葉的可用性與卷煙的安全性[J].煙草科技,2000(8):3-6.

[4] R ichard A J,Dean W W.Applied Multivariate Statistical Analysis(6 th Edition)[M].Hongkong:Pearson Education Asia Ltd.,2007:291-296.

[5] NelD J,Vander Merwe C A.A solution to the multivariate Behrens-Fisher problem[J].Comm unications in Statistics–Theory and Methods,1986,15:3719-3735.

[6] Krishnamoorthy K,Yu J Modified Nel,Van der Mer we.Test for the multivariate Behrens-Fisher problem[J].Statistics&Probability Letters,2004,66:161-169.

[7] Box G E P.Prob lem s in the analysis of growth and wear curves[J].Biometrics,1950(6):362-389.

[8] Filliben J J.The probability plot correlation coefficient test for normality[J].Technometrics,1975,17(1):111-117.

[9] Chou YM,Mason R L,Young J C.Power comparisons for a Ho telling’s T2statistic[J].Communications in Statistics,PartB-Simulation and Computation,1999,28:1031-1050.

[10]杜文,譚新良,易建華,等.用煙葉化學成分進行煙葉質量評價[J].中國煙草學報,2007,13(3):25-31.