網格資源共享策略的最優反應動態模型

李志潔，王存睿

（大連民族學院計算機科學與工程學院，遼寧大連 116600）

網格資源共享策略的最優反應動態模型

李志潔，王存睿

（大連民族學院計算機科學與工程學院，遼寧大連 116600）

圍繞網格環境中用戶的資源共享策略，應用進化博弈理論中的最優反應動態機制，建立了網格用戶最優反應動態模型并結合算例對網格用戶共享策略的發展變化趨勢進行了分析。研究結果顯示有限理性的網格用戶不能實現網格資源的最大化共享，需要結合其特殊性對原有的資源管理模式進行改進，以適應網格的實際情況。

網格;進化博弈;最優反應動態

網格環境［1－4］中參與者需要共享彼此多余的資源，要讓用戶隨心所欲地共享網格中的各種資源，還必須解決資源共享的不確定性問題。網格資源分配屬于動態系統，系統狀態隨時在變化，這就迫使網格實體在不完全信息情況下做出共享決策，這樣的決策必然帶有博弈的成分，因而可以用博弈論的模型加以分析。博弈論中一個重要的分支—進化博弈論（Evolution Game Theory）［5－7］是受到生物進化理論的啟發而發展起來的。進化博弈論假設博弈方按照生物或者社會的方式反復進行博弈，改善了傳統博弈分析的多重均衡問題，因而可對群體行為的動態調整過程進行更為全面的分析，加強博弈分析的理論基礎。進化博弈分析中模擬有限理性博弈方學習博弈和調整策略過程的一個典型機制就是最優反應動態。本文將利用最優反應動態機制深入研究網格資源共享問題，其目的不在于給出用戶的最優策略選擇，而在于從資源配置入手研究動態關系的優化，分析有限理性用戶組成的網格群體的策略調整過程、趨勢和穩定性，這樣才有可能抓住導致網格資源管理復雜性的主要環節，打破制約網格技術邁向實用化的主要瓶頸。

1 最優反應動態

進化博弈理論強調系統達到均衡的動態調整過程，認為系統的均衡是達到均衡過程的函數，即均衡依賴于達到均衡的路徑。一些學者曾提出了用于描述不同動態過程的動態機制。而本文所采用的是最優反應動態（Best－response Dynamics）機制［8］。所謂最優反應動態是指少數有快速學習能力的有限理性博弈方之間的重復博弈和策略進化。這種分析框架的理性假設為:博弈方具有相當快的學習能力，即使在復雜局面下準確判斷分析和運用預見性的能力稍差，也能對不同策略的結果作出比較正確的事后評估，并進行相應的策略調整。因此已知給定的上一輪博弈結果，各個博弈方本次博弈都能找到針對前期博弈結果的最佳反應策略。最優反應動態假設博弈方雖然缺乏分析動態關系和預見能力，但是能夠立即總結上一階段的博弈結果，并相應的調整策略。這些博弈方的策略調整雖然針對上一期對手是正確的，但對當前的對手策略不一定正確，因為對手的策略也在調整，而這正體現出了博弈方的有限理性和缺乏預見的能力。在最優反應動態機制下，每個博弈方與對手反復進行博弈的過程中如果出現策略的收斂，即趨向一于個唯一的穩定狀態，那么就得到最終的博弈均衡解，即進化穩定策略（Evolutionary Stable Strategy，ESS）。進化穩定策略意味著博弈方采用特定策略的比例達到該水平之后不再發生變化。此時最優反應動態就不再要求任何博弈方改變策略，這不僅是單個博弈方的策略穩定性，而且是群體意義上的策略穩定性。當群體中所有個體都選擇進化穩定策略時群體所處的狀態，就稱為進化穩定狀態，此時系統所達到的均衡稱為進化穩定均衡。進化穩定策略ESS的定義如下［9］:設s是博弈G的一個策略組合，如果存在任意小的ε，對任意的s'≠s和ε∈（0，1］，滿足

則稱s是一個“進化穩定策略”。在上述不等式中，表達式f（策略1，策略2）表示博弈方在雙方策略為（策略1，策略2）時的得益。在此定義中，ESS代表一個群體抵抗變異侵襲的一種穩定狀態，當主導策略s受到少量（ε%）變異策略侵襲時，定義中的不等式要求主導策略嚴格優于變異策略。

2 網格資源共享問題的博弈框架

2.1 網格資源共享問題

網格計算通過利用大量異構計算機的未用資源，為解決大規模的計算問題提供了一個模型。這樣，網格計算就形成了一個多用戶環境。而資源管理往往假設網格用戶都是完全理性的，在策略選擇上不會犯錯誤。而網格的異構性、動態性和協同性使得網格參與者無法滿足完全理性的要求，故以計算資源（CPU）為核心的資源共享存在以下難題:在資源共享過程中，每個參與的用戶是有限理性的，這意味著參與者往往不能或不會采用完全理性條件下的最優策略，存在著對其他用戶理性的信任問題，或者說在貢獻本地資源的同時懷疑其他用戶可能不共享資源。因此，資源共享具有不確定性，協調網格用戶的共享策略是經常遇到的難題。本文采用進化博弈的理論方法研究網格用戶的資源共享問題。在網格參與者策略選擇的過程中，個體收益與群體其他成員的收益之間具有緊密聯系。資源配置博弈的本質是動態的你得我失，未必均衡，但長期的博弈行為可能出現穩定的結果，形成各得其所的策略均衡。因此，建立基于進化博弈理論的網格資源配置模型，尤其是引入動態均衡概念，必將改善網格這種復雜系統的資源管理能力，獲得有效的資源共享。

根據進化博弈模型的思想，本文所要解決的網格資源共享是一個研究網格用戶的共享策略隨時間變化的動態博弈系統，重點關注用戶共享策略變化的篩選過程。該系統具有如下特點:①對稱博弈，雖然網格用戶在選擇出價策略時要面其它所有用戶，但總可以假設博弈是在成對的用戶之間進行的;②策略調整，可供網格用戶選擇的有兩種共享策略，一種是共享本地資源的策略，另一種是不共享本地資源的策略;③學習速度快，指的是網格用戶雖然缺乏預見能力，但是能給立即對上一期博弈的結果進行總結并調整本期策略;④收益導向，網格用戶在反復進行的博弈中，總會選擇能夠獲得最大收益的策略。關于網絡的拓撲圖，本文做了如下假定。假設共有N個網格用戶處于如圖1所示的圓周上的N個位置，每個用戶都與其左右鄰居反復博弈。圖中實線表示兩個用戶之間有網絡連接，可以進行博弈，虛線表示期間有若干個用戶。

圖1 網格用戶的網絡拓撲圖

2.2 博弈框架

有限理性下的網格資源共享是一個需要不斷學習的過程。進化博弈實際上就是有限理性個體組成的特定群體內成員間的反復博弈，來達到進化穩定均衡。要對網格資源共享博弈進行有限理性分析，必須先確定分析框架，包括理性層次和最優反應動態策略調整模式，以及博弈方群體的規模、分布和相互博弈方式。對于第一個方面，我們假設網格用戶雖然缺乏分析交互動態關系和預見能力，但是能夠立刻對上一階段的博弈結果進行總結，并作出相應的策略調整，即每一次用戶的調整都是針對其他用戶的策略作出最優反應。對于第二個方面，我們假設共有N個網格用戶分別處于圓周上的N個位置，每個用戶都與其左右相鄰的兩個用戶反復博弈如圖1所示。既然每個用戶都是有限理性的，那么在初次進行博弈時每個位置的用戶都既可能采用不共享策略，也可能采用共享策略。因此，初次博弈總共有2N種可能的情況。下面對這些網格用戶根據最優反應動態進行策略調整的規則作一些分析。

為了簡化研究問題，先把博弈系統中進行共享博弈的網格用戶群抽象為兩個用戶的群體，他們都是有限理性的博弈方，在出價博弈過程中，假定每個網格用戶都面臨兩種策略選擇，即共享策略和不共享策略，網格用戶選擇不同的策略所獲得的得益水平由圖1給出，由此構造一個隨機配對的博弈框架，可用圖2所示的2×2矩陣來表示。這種博弈的特征是兩個博弈方在策略和得益方面都是對稱的，因此，一個用戶究竟是在網格用戶1的位置博弈還是在網格用戶2的位置博弈并沒有區別。

圖2 網格用戶選擇共享策略的得益矩陣

圖2中A策略是不共享策略，B策略是共享策略。P1是網格用戶均選擇不共享策略時博弈雙方所獲得的得益水平，P4是網格用戶均選擇共享策略時博弈雙方所獲得的得益水平，P2是選擇不共享策略的用戶遇到選擇共享策略的用戶時所獲得的得益水平，P3是選擇共享策略的用戶遇到選擇不共享策略的用戶時所獲得的得益水平。在網格資源共享過程中，如果博弈雙方都采用相同的策略，那么他們獲得的得益水平是一樣的，都為P1或P4，而且P4＞P1。而如果博弈雙方采用不同得策略，則不共享資源的網格用戶必然侵占了選擇共享策略用戶的部分資源份額，因此不共享資源的用戶所獲得的得益必然大于共享資源用戶的得益，即P2＞P3。通過納什均衡分析可以確定該博弈有兩個純策略納什均衡（A，A）和（B，B），后者明顯優于前者。如果用戶是完全理性的，那么博弈結果應該是（B，B）。但是在有限理性的制約下，網格用戶事先并不知道哪種策略最好，經過反復博弈，采用共享策略的用戶可能轉向不共享策略，轉向不共享策略的用戶也可能回到共享策略，這導致無法預測這個博弈的結果。下面對求解該博弈的進化穩定均衡進行分析。

令xi（t）為在t時期用戶i的鄰居中采用A策略鄰居的數量，該數量最多為2個。故第t期如果用戶i采用A策略，那么得益為xi（t）·P1+［2－xi（t）］·P2;如果用戶i采用B策略，那么得益為xi（t）·P3+［2－xi（t）］·P4。下面我們分三種情況對第t+1期的用戶策略進行討論。

①如果xi（t）·P1+［2－xi（t）］·P2＞xi（t） ·P3+［2－xi（t）］·P4，那么第t期用戶i采用A策略的得益大于采用B策略的得益，即xi（t）＞2 （P4－P2）/（P1－P2－P3+P4）時，用戶i在第t+1期會采用A策略。

②如果xi（t）·P1+［2－xi（t）］·P2＜xi（t） ·P3+［2－xi（t）］·P4，那么第t期用戶i采用B策略的得益大于采用A策略的得益，即xi（t）＜2 （P4－P2）/（P1－P2－P3+P4）時，用戶i在第t+1期會采用B策略。

③如果xi（t）·P1+［2－xi（t）］·P2=xi（t） ·P3+［2－xi（t）］·P4，那么第t期用戶i采用A策略的得益等于采用B策略的得益，即xi（t）=2 （P4－P2）/（P1－P2－P3+P4）時，用戶i在第t+1期會采用與第t期同樣策略。

根據以上分析，網格用戶的最優反應動態方程可以表示如下:

其中，Strategy（t）表示第t期用戶i采用的策略，w為臨界值2（P4－P2）/（P1－P2－P3+P4），由上述三種情況分析得出。式（2）表明，當網格用戶采取A策略的得益大于采取B策略的得益時，在下一期網格用戶都能作出最優反應，即都采取A策略;反之，則在下一期網格用戶都將采取B策略。當二者相當時，采取A策略的用戶個數保持不變。

3 算例分析

3.1 進化算法

根據最優反應動態機制，用戶根據上期博弈的結果確定本期博弈的共享策略。初次博弈時，N個用戶的共享策略隨機指定，可為共享策略和不共享策略。每個用戶分別與其左右鄰居進行反復博弈。按照編號有序的原則，如果當前為用戶i，則下一個用戶的編號為（i mod N）+1，而前一個用戶的編號為（（（i mod N）+N－1）mod N）+1。本文進化博弈中用戶共享策略選擇的最優反應動態算法可以描述為:

①博弈開始時，初始化用戶數量N及得益矩陣P1，P2，P3，P4;

②隨機指定用戶的初始策略，并計算臨界值w;

③for每個用戶i do

統計鄰居中采用A策略的用戶數量k;

if k＞w then

用戶下一期采用A策略;

else if k＜w then

用戶下一期采用B策略;

else

用戶下一期采用與本期相同的策略;

④if本期博弈結果與上期結果相同then

轉步驟⑤;

else

返回步驟③;

⑤算法結束.

3.2 實驗結果

為了對最優反應動態算法的博弈過程和結果進行分析，下面通過一個典型的算例，對算法執行過程中用戶策略的動態調整和穩定結果做進一步的討論。設網格系統中有16個有限理性的用戶，他們具有相同的得益矩陣如圖3所示，且只有共享和不共享兩種策略可以選擇。

圖3 網格用戶博弈的得益矩陣

N個用戶的初始策略隨機指定為s1=B，s2= B，s3=B，s4=B，s5=B，s6=B，s7=A，s8=B，s9= B，s10=A，s11=A，s12=B，s13=B，s14=B，s15=B，s16=A。根據得益矩陣，可計算臨界值w=0.667。為了直觀的表示用戶的初始策略，本文繪制了對應的餅圖如圖4所示。圖4中共有16個扇區分別表示16個用戶的策略，其中分離出來的扇區表示該用戶選擇的是不共享策略，而沒有分離的扇區則表示選擇的是共享策略。

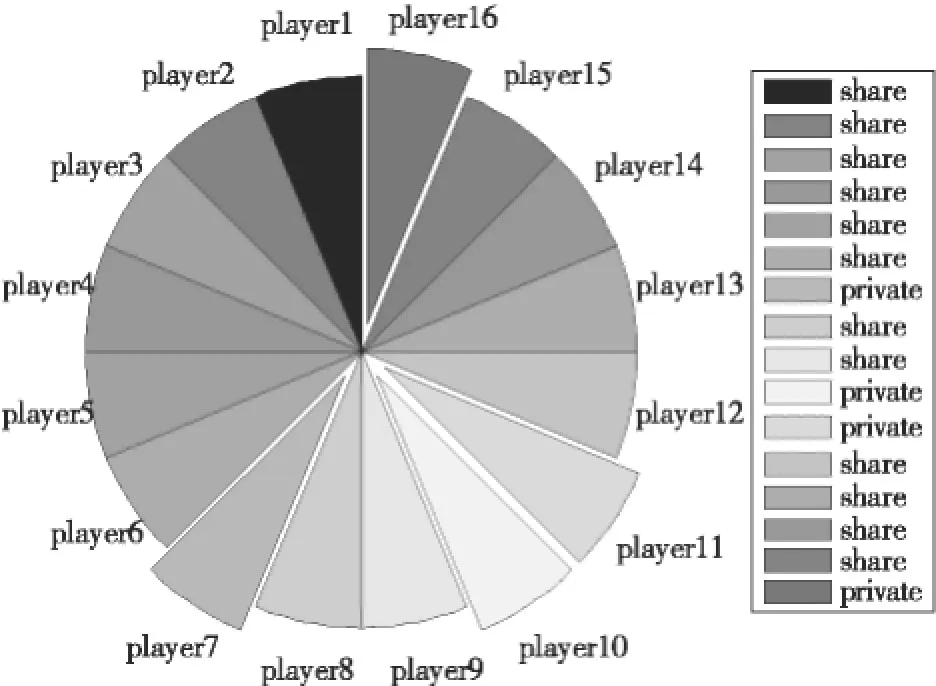
圖4 網格用戶初始策略餅圖

表1和表2給出了網格用戶的進化博弈過程。從下面兩個表中的結果可以看出，進化博弈一共進行了8個時期，從最初個別用戶的扇區分離進化到所有用戶的扇區分離，由于第9期與第8期的結果一樣，所以算法結束。前面我們已經假定了網格用戶是具有快速學習能力的有限理性群體，故進化博弈的收斂速度很快。根據最優反應動態機制，每期用戶都會針對上一期的博弈結果而調整共享策略，以達到最大化自己得益的目的。經過反復的策略調整，最終所有用戶都收斂到了采用不共享策略的穩定狀態，此時最優反應動態不再要求任何用戶改變策略，這個不僅僅是單個用戶的策略穩定性，而且是群體意義上的策略穩定性。這個算例只是眾多例子中的一個，但是其折射出有限理性用戶在資源共享過程中的一個趨勢，即不共享自己的資源。即使都采用共享策略的得益大于不共享策略，受到理性層次的制約，網格用戶仍然會收斂到不共享的穩定狀態，這也正是有限理性和完全理性的區別所在。雖然網格的最初目的是共享所有參與者的資源，提高資源利用率，但現實情況恰恰相反，如果沒有很好的激勵機制來維護網格系統，最終的結果必然是沒有用戶愿意貢獻自己的資源。

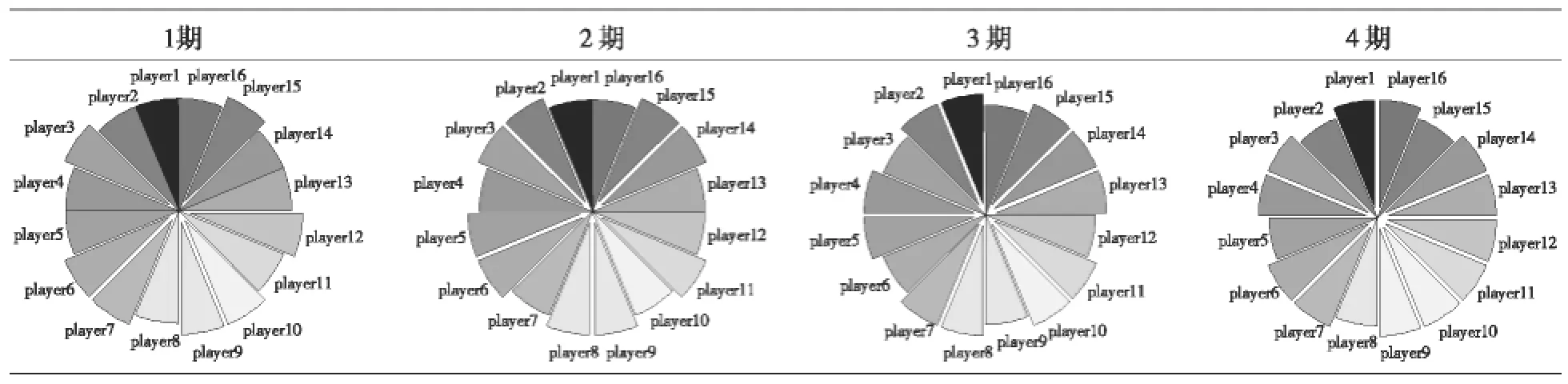
表1 第1期至第4期的網格用戶進化博弈過程

表2 第5期至第8期的網格用戶進化博弈過程

4 結論

在博弈框架下研究網格用戶共享策略的動態演化過程，從網格參與者的角度，深入研究有限理性網格用戶策略調整的過程和動態穩定性之間的關系，研究內容可為網格實際應用中資源配置進化博弈的定量表達提供理論依據。目前網格用戶的資源共享過程非常適合使用最優反應動態機制來分析。通過模擬實驗表明，所有用戶都采取不共享策略是系統的最容易出現的穩定狀態。這與網格的共享精神是相背離的。所以，網格用戶受到理性層次的制約，并不能很好的發揮提高資源利用率的作用。為此，需要向網格系統注入合適的激勵機制以維護系統的良好運行。如何在多用戶的動態環境中協調資源的共享使用，實現資源的優化配置，這樣的激勵機制的方法與規則是有待深入研究的問題。

［1］FOSTER I，KESSELMAN C，TUECKE S.The anatomy of the grid:Enabling scalable virtual organizations［J］.International Journal of Supercomputer Applications，2001，15（3）:200－222.

［2］YANG Guangwen，JIN Hai，LI Minglu，et al.Grid computing in China［J］.Journal of Grid Computing，2004，2（2）:193－206.

［3］FOX G.Grid computing environments［J］.IEEE Computational Science and Engineering，2003，5（2）:68－72.

［4］KRAUTER K，BUYYA R，MAHESWARAN M.A Taxonomy and Survey of Grid Resource Management System for Distributed Computing［J］.Software:Practice and Experience，2002，32（2）:135－164.

［5］FATIMA S S，WOOLDRIDGE M，JENNINGS N R.A comparative study of game theoretic and evolutionary models of bargaining for software agents［J］.Artificial Intelligence Review，2005，23（2）:185－203.

［6］ANTAL T，SCHEURING I.Fixation of strategies for an evolutionary game in finite populations［J］.Bulletin of Mathematical Biology，2006，68（8）:1923－1944.

［7］ALTMAN E，BARMAN D，EL AZOUZI R，et al.Pricing differentiated services:A game－theoretic approach［J］.Computer Networks，2006，50（7）:982－1002.

［8］謝識予.經濟博弈論［M］.2版.上海:復旦大學出版社，2002.

［9］王鑫，李研.區域電力市場中發電商競價策略的最優反應動態模型［J］.華北電力大學學報，2006，33 （6）:51－54.

Best－response Dynamic Model for Resource Sharing Strategy in Grid

LI Zhi－jie，WANG Cun－rui
（School of Computer Science＆Engineering，Dalian Nationalities University，Dalian Liaoning 116605，China）

Concerning the resource sharing strategy of grid user，the dynamics model of rational user based on the best－response dynamic mechanism has been established.With typical case，the evolution trend of user sharing strategy has been analyzed.The result showed that the maximize sharing of grid resources cannot be achieved because of the bounded rationality of grid user.Thus，the original resource management should be improved to adapt to the actual situation of grid environment.

Grid;evolutionary game;best－response dynamics

TP393

A

1009－315X（2011）03－0291－05

2011－03－23

中央高校基本科研業務費專項資金資助（DC10040110）;遼寧省教育廳科學技術研究項目支持（2010044）;大連民族學院博士啟動基金項目支持（20086205）。

李志潔（1978－），女，黑龍江雞西人，副教授，博士，主要從事智能算法研究。

（責任編輯 劉敏）