束縛水飽和度對水力壓裂非達西氣井產能的影響

李文學 馬新仿 王玉敏

（1.中國石油大學石油工程教育部重點實驗室，北京 102249；2.大慶油田有限責任公司第一采油廠，黑龍江大慶 163001）

非達西滲流在石油工業的應用始于19世紀60年代。起初，通常認為非達西滲流只存在于高速流動條件下。后來許多學者發現在一定的條件下氣體在儲層中的流動也存在非達西滲流［1］。高速非達西滲流產生附加壓降，會大大降低氣井的產能［2-3］。當儲層存在非達西滲流時，含水飽和度的影響不能忽略。含水飽和度對非達西滲流的影響存在兩種情況：一是儲層中只存在束縛水，即含水飽和度為束縛水飽和度。這種情況下，氣井在生產過程中為氣體單相滲流，含水飽和度對非達西滲流的影響主要是對非達西系數的影響；二是儲層中既存在束縛水，也存在可動水，此時氣井在生產過程中為氣水兩相滲流。非達西效應對水的影響要遠遠小于對氣的影響，甚至可以忽略［4］。為了研究單相氣體流動條件下的非達西效應，這里只考慮束縛水飽和度的影響，即認為地層和裂縫內氣體都是單相流動。

1 非達西滲流的基本原理

流體在多孔介質中流動可以用達西定律表示為［5］

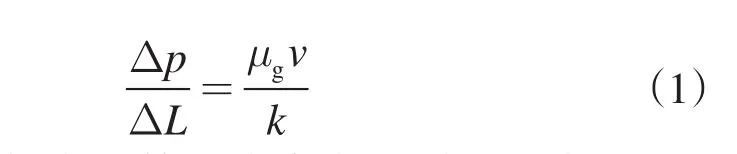
在滲透率較大的儲層或水力壓裂裂縫內，由于氣體的高速流動，其滲流規律可能不再適用于達西滲流，而是非達西滲流。Forchheimer［6］最早提出了描述氣體非達西滲流的方程，后來Cornell等人［7］又對該氣體的滲流方程進行了完善和改進，得到了新的氣體非達西滲流方程

非達西滲流方程和達西滲流方程的不同之處在于多了速度的二次項，并且有一個關鍵的參數，即非達西滲流系數β。所以要研究非達西效應對氣井產能的影響，首先要計算不同條件下的非達西滲流系數β，然后再計算其對產能的影響。

2 非達西滲流系數β的計算

非達西滲流系數是多孔介質的一個重要性質，目前有很多的經驗公式可以計算。為了研究單相氣體流動條件下的非達西效應，這里只考慮束縛水飽和度的影響，即認為地層和裂縫內氣體都是單相流動。

2.1 儲層內非達西滲流系數β的計算

對于儲層內非達西滲流系數β的計算，目前主要是根據室內巖心驅替實驗的結果回歸得到的公式。雖然在不同的實驗條件下得到的公式不同，但表達式都一樣，只是系數隨條件的不同而變化，目前使用比較多的是Geertsma公式［8］

Geertsma公式考慮了儲層內束縛水飽和度對非達西滲流系數的影響，同時實驗時采用了不同性質的巖心，包括疏松砂巖和致密砂巖等，具有較好的適用性。

2.2 支撐裂縫內非達西滲流系數β的計算

對水力壓裂氣井，由于裂縫充填支撐劑，不存在束縛水。所以裂縫內的流動是單相流還是多相流取決于儲層內的水是束縛水還是可流動的水。由于這里只考慮束縛水飽和度對非達西滲流的影響，即儲層和裂縫內均為氣體單相流動，同時考慮氣體在儲層和裂縫中都是非達西滲流，所以裂縫內仍為氣體的單相滲流，如果考慮裂縫內氣體的非達西滲流，則非達西滲流系數β的計算可以采用下面的計算式［9］

其中，系數a、b、c的值由裂縫內支撐劑的粒徑決定，如果β系數的單位取m-1，kf的單位取10-3μm2，則a、b、c的取值見表1。

表1 不同支撐劑的粒徑條件下a、b、c 的取值

3 束縛水飽和度對非達西滲流系數β的影響

為了研究儲層內束縛水飽和度對非達西滲流系數β的影響，分別取束縛水飽和度從0到0.3，利用公式（3）計算了不同儲層滲透率下的非達西流系數（圖1）。可以明顯看出，在同一束縛水飽和度條件下，地層的滲透率越小，非達西滲流系數越大；而在同一儲層滲透率下，隨著束縛水飽和度的增加，非達西滲流系數也逐漸增加。地層滲透率越小，β系數增加的幅度越大，反之，增加的幅度越小。

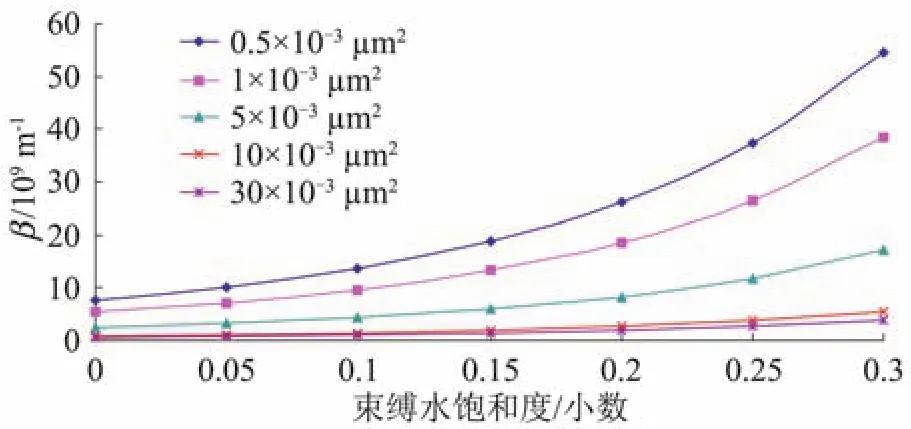
圖1 不同滲透率下束縛水飽和度對β的影響

4 束縛水飽和度對非達西滲流氣井產量的影響

為研究考慮非達西滲流條件下束縛水飽和度對氣井產量的影響，分別取儲層滲透率為5×10-3μm2、30×10-3μm2和50×10-3μm2進行計算，計算結果見圖2。

圖2 不同滲透率下束縛水飽和度對累積產量的影響

可以看出，當儲層滲透率較小時，束縛水飽和度對氣井累積產量基本上沒有影響。但是，隨著滲透率的增加，束縛水飽和度對累積產量的影響越來越大，當儲層滲透率為50×10-3μm2時，束縛水飽和度對累積產量的影響非常明顯。

另外，在給定滲透率條件下，隨著束縛水飽和度的增加，氣井累積產量下降幅度越大，說明非達西效應越明顯。其原因在于：對于低滲透儲層，由于滲透率較低，氣體在孔隙介質中的滲流阻力大，流動速度小，非達西效應不明顯或沒有，氣體的流動仍然是達西滲流。而對于中高滲透儲層，由于儲層的滲透率較大，氣體的滲流阻力小，流速大，這時氣體的流動逐漸偏離了達西滲流規律，出現了非達西滲流，并且滲透率越大，非達西效應越明顯，對氣井的產量影響也越大。

5 結論

（1）非達西流系數β隨束縛水飽和度的增加而增加，且滲透率越小，增加的幅度越大，而滲透率越大，增加的幅度越小。

（2）對于中高滲透的氣井，氣體的非達西效應比較明顯，生產時必須考慮束縛水飽和度對非達西效應和產量的影響。儲層滲透率越大，束縛水飽和度的影響越明顯。

（3）對于中高滲透儲層，束縛水飽和度越大，非達西效應越明顯，對氣井的產量影響越大。束縛水飽和度越大，累積產量下降的幅度越大。

符號說明

Dp為流體在油藏中流動的壓降，Pa；DL為流體在油藏中的流動長度，m；μg為油藏條件下氣體的黏度，Pa·s；v為氣體的流動速度，m/s；k為油氣藏滲透率，μm2；β為非達西滲流系數，m-1；ρg為油藏條件下氣體的密度，g/cm3；kr為儲層內氣水兩相時氣體的相對滲透率；φ為裂縫內支撐劑的孔隙度，小數；Swi為儲層孔隙內的束縛水飽和度，小數；kf為裂縫內的滲透率，μm2。

［1］ MIKSIMINS J L, LOPEZ-HERNANDEZ H D, BARREE R D. Non-darcy fow in hydraulic fractures: does it really matter? ［R］. SPE 96389, 2005.

［2］ 許少松，陳欽雷.井筒附近地層高速非達西滲流的數值分析［J］.石油大學學報：自然科學版，1994，18（5）：53-59.

［3］ 康曉東，李相方，程時清.考慮流動邊界影響的氣井非達西效應評價［J］.中國石油大學學報：自然科學版，2006，30（1）：82-85.

［4］ EVANS R D, HUDSON C S, GREENLEE J E. The effect of an immobile liquid saturation on the non-darcy flow coeffcient in porous media［R］. SPE 15066, 1987.

［5］ 葛家理，寧正福，劉月田，等.現代油藏滲流力學原理［M］.北京：石油工業出版社，2001.

［6］ FORCHHEIMER P. Wasserbewegung durch boden［J］. ZVDI, 1901, 27（45）: 26-30.

［7］ CORNELL DAVID, KATZ DONALD L. Flow of gases through consolidated porous media［J］. Industrial and Engineering Chemistry, 1953, 45（10）: 21-45.

［8］ GEERTSMA J. Estimating the coefficient of inertial resistance in fuid fow through porous media［J］. SPE Journal, 1974, 14（5）: 445-450.

［9］ COOKE C. Conductivity of fracture proppants in multiplelayers［R］. SPE 4117, 1972.