回歸原點 層層推進
2011-01-01 00:00:00汪雪明
小學教學參考(數學) 2011年6期
小學數學中概念是重要的基礎內容。傳統概念教學中往往“輕過程重結果”,現如今在新理念的影響下,又出現了只重視思維過程,對概念的結果及精確的表述往往過于弱化的現象,以至于學過之后,學生不能用簡潔、準確的語言表述。如何更好地處理概念形成的過程與結果?筆者以自己“中位數”的教學實踐為例,談談對概念教學的一些思考。
一、在本源情境中感知概念
每一個概念的產生都有它本源背景,追溯概念的來源、產生的緣由是學生形成概念的基礎,還可以加強知識間的聯系。因此,教師要創設一定的情境,在情境中逐步感知概念,從而引入概念教學。
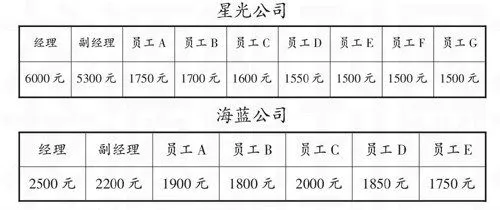
出示信息:海藍公司現有員工7名,人均月工資2000元。
星光公司現有員工9名,人均月工資2400元。
師:我的一位朋友在找工作時看到兩家公司招聘信息,工作環境與工作量都差不多,你會建議他選擇哪家公司?
生:選擇星光公司。
師:為什么?
生1:人均月工資2400元高于2000元。
生2:星光公司員工月平均工資多400元。
師:人均月工資2400元,是表示星光公司每個員工每月收入都是2400元嗎?
生3:不是,它是一個平均數。
出示工資表:
師:現在會選擇哪家公司?
生:海藍公司。
師:為什么又改變了呢?星光公司人均工資更高呀!
生4:因為星光公司經理、副經理工資特別高,將平均工資抬高了。
生5:海藍公司人員工資比較接近,最低工資都和星光公司的員工最高工資一樣。
師:對,6000元、5300元比其他數大得多,數學上稱為極端數。有極端數時平均數就不能準確反映職工工資一般水平,那選擇什么合適呢?(生討論匯報)
由于學生受已學知識的影響,習慣用總數或平均數為標準作選擇。教學中創設這樣一個與舊知產生沖突的情境,使學生在兩次矛盾選擇中感知原來知識的不足,需要用新的知識、方法來解決問題。教師不是直接給出概念,而是留足學生自主思考和發現的時間與空間,自然引入新概念的學習,使學生既真切感知中位數概念,又了解與已學的統計量之間的聯系。
二、在層層探索中理解概念
要真正建構概念,教師應提供豐富的素材,使學生充分感知,豐富其表象,并引導學生通過自主比較、分析、歸納、抽象等方法,使學生的頭腦中形成和理解概念,揭示概念的內涵,弄清概念的本質特征。
師:星光公司工資數的中位數是1600元,那海藍公司這組工資數的中位數又是多少呢?想一想,該怎么找?寫一寫,怎樣讓人一看就明白你寫的是中位數?
生1:1800,它在7個數的中間。
生2:不對,位置在中間不一定就是中位數,要排一排。
生3:1900,因為比它大的有3個數,比它小的有3個數。
生4:我是按從大到小排列后,再找出大小、位置在中間的數。
師:你們認為誰的方法比較好?(大多數同意生4的方法)
師:誰能用自己的話說說什么是中位數嗎?
生5:大小排在中間的數叫中位數。
生6:按從大到小排列后,最中間的數才叫中位數。
生7:也可以從小到大排列,最中間的數。
師:我的朋友最終選擇海藍公司,他的工資為1750元。這時,你們還能找出這組數的中位數嗎?
……
在初步感知中位數概念后,為了豐富其表象,出示大小順序錯亂的一組數,讓學生通過獨立思考找出中位數,并說出找的方法。學生想、找、說的過程,事實上已在逐步構建中位數的概念,又通過用自己的語言描述來弄清概念的內涵,進一步完善概念,加深對概念的理解。
三、在聯系比較中深化概念
概念的真正建構,不僅要通過從其具體事物及材料中抽象概括,弄清概念的內涵,還要在與其相關的概念比較中進一步深化,提示其內涵與外延,才能有效地、靈活運用概念來解決現實問題。
(學生初步感知一組數據中出現極端數時,平均數不能體現員工工資的整體水平)
師:海藍公司工資數據選擇哪個數能代表職工的整體水平?
生1:數據中沒有極端數,選擇平均數。
生2:中位數,剛好是中等水平。
師(出示統計圖呈現平均數、中位數):兩個數據

