粒子群算法與主成分析法在支持向量機回歸預測中的應用研究*

周方軍，呂文元

(上海理工大學 管理學院，上海 200093)

預測是國家、企業等組織制定政策和計劃的主要依據，因而預測的準確度是政策與計劃制定是否科學的前提。預測的方法有傳統的多元回歸預測，以及近幾年來發展起來的人工神經網絡預測[1]、灰色預測[2]。多元回歸預測模型簡單、易用性強，但難以處理高維、非線性模式；人工神經網絡雖然能夠較好地解決高維非線性預測的難題，但它需要大量的訓練樣本，且泛化能力不強，所以當可得到的預測樣本是小樣本，或者獲得大量樣本的成本很高時，就難免影響其實用性和經濟性；灰色預測雖具有短期預測能力強，可檢驗等優點，但其長期預測能力較差。Vapnik等人提出的支持向量機[3-4]是在統計學習理論基礎上發展起來的一種新的機器學習算法，是目前針對小樣本統計和預測學習的最佳理論，支持向量機具有完美的數學形式、直觀的幾何解釋和良好的泛化性能，解決了模型選擇與欠學習、過學習及非線性等問題，克服了收斂速度慢，易陷入局部最優解等缺點，因此支持向量機在分類和回歸中均表現出優越的性能。

1 支持向量回歸機的基本原理

支持向量回歸機[5]，主要由Vapnik提出的ε-支持向量回歸機(ε-SVR)和Scholkopf等提出ν-的支持向量回歸機(ν-SVR)等。本文采用Vapnik的ε-SVR支持向量回歸機。

支持向量機回歸實質是要在Rn空間尋找一個超平面函數y=wT·x+b，并使得該超平面與各樣本點的偏離最小，其中w是超平面n-1維法向量。考慮一個樣本集T={(x1T，y1)，…(xlT，yl)}∈(X×Y)，l為樣本數，xi是 n 維向量，y∈Rn。如果采用ε不靈敏函數作為誤差函數，當所有的樣本點到所求的超平面的距離都不超過ε時，如圖1所示，中間的實線表示ε的超平面，超平面兩邊的ε區域為超平面的ε帶。

可以想象，一個最優的超平面應該是能夠以最小的ε帶包含訓練集中所有樣本點的超平面。為求得最優超平面，借鑒支持向量機分類的思想，可將其轉化為一個二分類的問題：選擇合適的 ε(ε≥minε)，分別給每個樣本點的y值加上ε或減去ε，構造新的正負兩類樣本點：D+=(，yi+ε；zi=+1)(i=1，2， …l)，D-=(，yi-ε；zi=-1)(i=1，2，…l)。考慮會有個別樣本點到超平面距離大于ε影響求解最優超平面的情況，引入松弛變量 ξi，ξ*i和懲罰參數C，構造并求解問題：

引 入 Lagrange 乘 子 ，a(*)=(a1，a*1…al，a*l)≥0， 構 造Lagrange函數，求式(1)的對偶問題得：

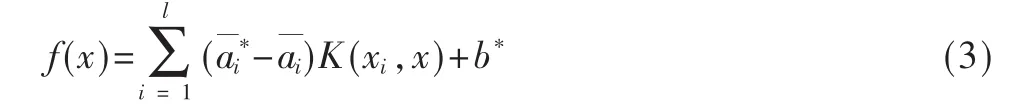
其中

式(2)～ 式(4)中 K(xi，xj)是 核 函 數 ， 其 值 為 向 量 xi和xj在特征空間的 φ(xi)和 φ(xj)中的內積，φ(xi)，φ(xj)為映射函數。核函數的作用是當樣本點在原空間線性不可分時，可以通過映射函數映射到高維空間，從而達到線性可分的目的，但實際應用中映射函數的顯式表達式很難找到，觀察式(2)～式(4)中只用到了映射在高維空間的點積，而核函數的特點就是能使變量在低維空間核函數值等于其映射到高維空間的點積值，從而實現不需要知道顯式映射函數達到向高維空間映射的目的。任何滿足Mercer條件的函數均可作為核函數。

2 粒子群算法基本原理

微粒群算法最早是在1995年由美國社會心理學家Kennedy和Russell[6]共同提出，其基本思想是受鳥群覓食行為的啟發而形成的。PSO算法把優化問題的解看作是D維空間中一個沒有體積沒有質量的飛行粒子，所有的粒子都有一個被優化目標函數決定的適應度值，而速度決定每個粒子的飛行方向和距離，粒子根據自己先前達到的最優位置和整個群體達到的最優位置來更新自己的位置和速度，從而向全局最優位置聚集。粒子根據以下公式來更新自己的速度和位置：

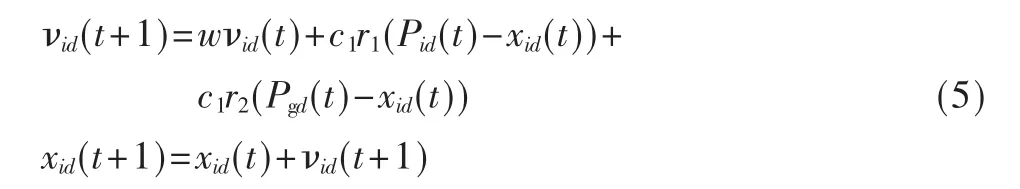
式中，下標i代表第i個粒子，下標d代表速度或位置的第 d維，t代表迭代代數，w代表慣性權重系數，c1和 c2是學習因子， 通常 c1，c2∈[0，4]，r1，r2是介于[0，1]之間的隨機數，Pid是粒子Pi在第 d維個體極值坐標，Pgd是粒子群體在第j維的全局極值坐標。從式(5)可知，w越大全局探測能力越強；w越小則局部探測能力越強。因此可以讓w隨著迭代次數的增加，而動態地減少，以保證算法有較大的機率收斂于全局最優解。但是在算法執行過程中，隨著w的減少，也在一定程度上導致后期收斂速度降低，從而影響全局收斂性能。為了克服這種缺陷，Clerk構造了帶收縮因子K的改進 PSO模型[7]，試驗結果表明收縮因子K比慣性權重系數w能更有效地控制微粒的飛行速度，同時增強了算法的局部搜索能力，模型如下：

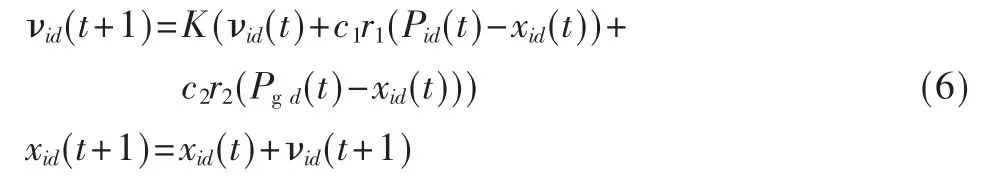
經檢驗，兩組護生操作考試成績不符合正態分布，故采用非參數檢驗Wilcoxon秩和檢驗，對照組護生成績中位數為83.37分，試驗組護生成績中位數為89.73分，兩組比較：Z=-6.501，P=0.000。

3 主成分析原理

主成分析[8]是利用數學上處理降維的思想，將實際問題中的多個相關性較高的指標設法重新組合成一組新的少數幾個互不相關的綜合指標來代替原來指標的一種多元統計方法，通常把轉化生成的綜合指標稱為主成份，其中每個主成份都是原始變量的線形組合。主成份要盡可能多地反映原來指標的信息，而且要有較好的解釋意義。降維的步驟：(1)將原始數據標準化以消除量綱影響；(2)計算變量的相關系數矩陣 R=(rij)p′p，其中 rij(i，j=1，2，…，p)為原來變量 xi與 xj的相關系數；(3)計算R的特征值及相應的特征向量，即 λ1≥λ2，…≥λp≥0然后分別求出對應于特征值 λi的特征向量 ai(i=1，2，…，p)，且 ai是正交單位特征向量；(4)寫出主成份 Fi=a1iX1+a2iX2+…+apiXp(i=1，…，p)。

4 應用實例

試驗從UCI上選取美國波斯頓地區1993年城鎮住房數據作為試驗數據[9]。試驗步驟如下：

(1)應用主成分析法降維

由于統計軟件SPSS提供了主成份分析功能，而且具有采用交互式、圖形化操作界面、結果圖形化輸出、直觀性強等優點，故本文采用SPSS16.0作為降維工具，表1為最大方差旋轉后的因子載荷圖，從表中可以看出，7個主成份都有很好的解釋意義(載荷絕對值＞0.5，說明變量與主成份存在相關性)。主成份1為城鎮生活環境，主成份2為治安環境，主成份3為人口密度，主成份4為人口層次，主成份5為是否有河流，主成份6為商業環境，主成份7為教育發展水平。

表1 主成份載荷旋轉

(2)應用粒子群算法優化支持量機參數

支持量機回歸待優化的參數有懲罰參數C和e帶參數 e，采用高斯徑向基函數 K(xi，xj)=exp(-γ‖xi，xj‖2)作為SVM模型的核函數。選取降維后試驗數據前352個樣本作為訓練樣本，后100個樣本作為預測樣本。設C ∈[1，500]，ε∈[0.01，10]，Vid_max=Xid_max，c1=2.8，c2=1.3，種群規模為30，最大迭代次數為30，采用3折交叉驗證模式下的均方誤差(MSRE)作為評估粒子的適應度函數。優化后得到最優C=375.754，ε=0.175，最優目標函數的適應度值MSRE=7.4801。

(3)應用e-SVM進行回歸預測

本文把量子群優化算法和主成分析降維的方法應用于支持向量機的回歸預測中，試驗結果表明此法能顯著提高支持向量機的預測精度，同時也表明了支持向量機在非線性、高維模式下的良好預測性能。

[1]閻平凡，張長水.人工神經網絡與模擬進化計算[M].北京：清華大學出版社，2006.

[2]韋康南，姚立綱等.基于灰色理論的產品壽命預測研究[J].計算機集成制造系統，2005(10)：1491-1495.

[3]VAPNIK V N.The nature of statistic learning theory[M].New York： Springer， 2005.

[4]VAPNIK V N.Estimation of dependencies based on empiric[M].Berlin Springer-Verlag，2003.

[5]鄧乃揚，田英杰.數據挖掘中的新方法-支持向量機[M].北京：科學出版社，2004.

[6]KENNEDY J，EBERHART R.Particle swarm optimizat[A].Proc IEEE IntConf.on Neural[C].Perth，1995.1942-1948.

[7]CLERK， M.The swarm and the queen： Towards a deterministic and adaptive particle swarm optimization[A].1951-1957.1990.Proc.CEC 1999.

[8]林海明.對主成分分析法運用中的十個問題的解析[J].統計與決策(理論版)，2007(8)：16-18.

[9]http：//archive.ics.uci.edu/ml/index.html 1993.07.