井筒流體中與溫度相關的摩擦力的研究

編譯:侯冠中 (中國海洋石油監督監理技術公司)

審校:侯秀蘭 (中國石油大學 (北京)石油天然氣工程學院)

井筒流體中與溫度相關的摩擦力的研究

編譯:侯冠中 (中國海洋石油監督監理技術公司)

審校:侯秀蘭 (中國石油大學 (北京)石油天然氣工程學院)

不斷增加的井的可達距離是現代鉆井中最重大的發展之一。與鉆井和完井階段有關的井筒摩擦力起著主要作用。然而,石油工業使用簡單的單參數庫侖摩擦力模型來分析井的摩擦力,而沒有考慮溫度的影響。Stavanger大學開展摩擦力研究已有許多年,對機械、黏性、溫度和材料的摩擦效應有更深入的了解。本文展現了這項工作的一些成果。測量了許多從泥漿賣主得到的水和油基鉆井泥漿。包含加熱單元的測試設備用于研究溫度對摩擦力的影響。報告上的數據的溫度范圍是10～100℃。正如所預期的,油基流體的摩擦因數比水基流體的低。除了一種泥漿顯示在50℃以上時摩擦力幾乎是常量外,所有流體的摩擦因數隨著溫度的升高而增加。在不同的流體之間有相當大的差異。本文分別測量了鋼鐵與鋼鐵、鋼鐵與混凝土和鋼鐵與巖石的摩擦因數。由于巖石材料表面粗糙度較高,鋼鐵與巖石具有較高的摩擦力。推導了與溫度相關的摩擦因數的方程式,油田實例應用結果顯示,溫度對摩擦力的影響相當大。

摩擦力 摩擦因數 溫度 模型

1 引言

1699年,Amontons研究并建立了兩個摩擦定律。Coulomb通過研究靜摩擦和動摩擦建立了第三個摩擦定律。這三個定律是:

◇摩擦力與施加負荷是直接成比例的;

◇摩擦力不依賴于接觸的表面面積;

◇動摩擦力不依賴于速度。

在那個時代這些定律的結果暗示,摩擦力是由聯結不平整引起的,即開始運動時必須有一個力來克服它。

2 摩擦因數

Antoine Parent通過定義以下關系式把Amontons的工作成果引入到力學:

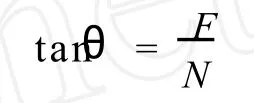
式中,θ是平面的傾角;F是切向力;N是法向力。后來Euler指出:

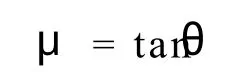
式中,μ是摩擦因數。

2.1 現在使用的摩擦因數的定義

摩擦因數是施加在接觸物體上的摩擦力與法向負荷的比。

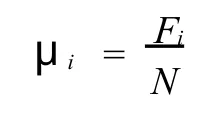
式中,i是靜止或運動;F是摩擦力;N是法向力;μ是摩擦因數。

摩擦因數受許多因素影響,如施加的負載、濕度、表面粗糙度、溫度、黏度和速度。因此測量時因數的表格中應當包含環境因素。

2.2 靜摩擦力和動摩擦力

摩擦力有動或靜兩種特征。靜摩擦力是當兩個物體不相互運動時與外加力相互抵消的力。動摩擦力是當相互接觸的物體相對運動時與牽引力或推力相抵消的力。靜摩擦力和動摩擦力的典型狀態如圖1所示。

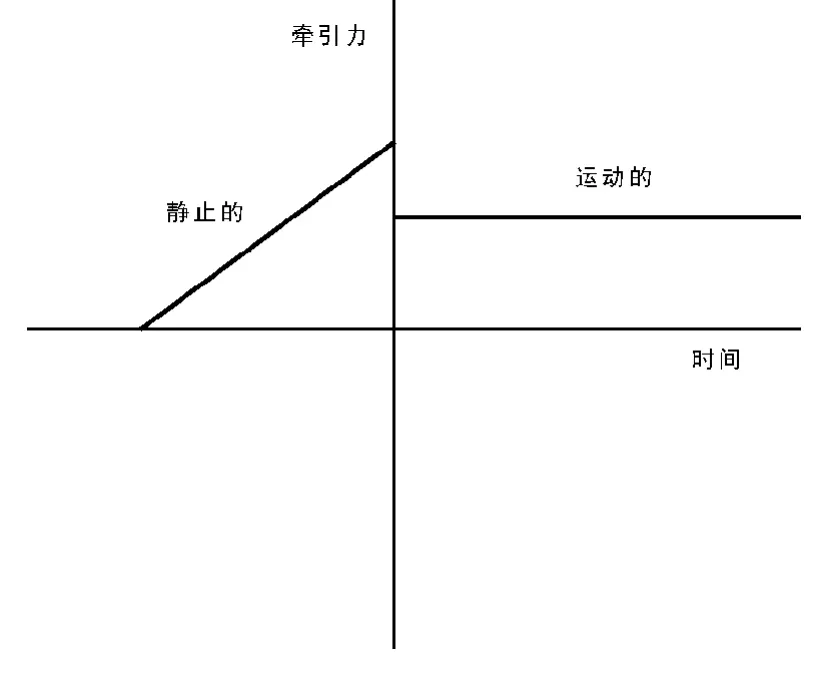
圖1 牽引力是時間的函數。靜摩擦力在左邊,動摩擦力在右邊

2.3 接觸面積

兩個基本摩擦定律說明了摩擦力與負荷成正釋,且與滑動面的面積無關。1950年,Bowden和Tabor對Amontons發現的摩擦定律給出了物理解釋。他們提出甚至最光滑的平面也有粗糙,它們實質上比分子的尺寸大。這意味著當兩個表面放在一起時,它們不會整個表面都有接觸。這種不規則將會滿足彼此,并且在接觸點上實際的或真的接觸面積是接觸點的總和。

由于不規則,有效接觸面積比總的或表面面積小 (圖2)。一般認為,實際接觸面積與壓著兩個表面的法向力N是成正比的。這引出了下面的關系式:

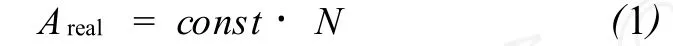
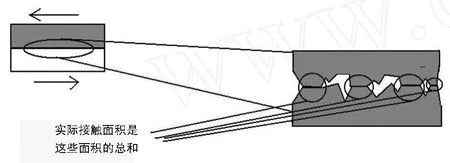
圖2 摩擦因數取決于比接觸表面積小的實際接觸面積

2.4 金屬間摩擦力

1964年,Bowden發現較硬的金屬會形成表面較光滑的金屬。由于層可能會切斷,金屬間的層也影響摩擦阻力。總的切向力是為了剪切實際接觸面積上的薄膜:

帶入方程式 (1)可得:

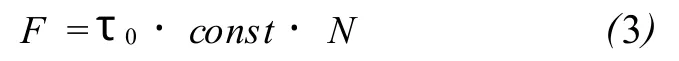
定義摩擦因數,μ=const·τ0,則方程式 (3)可以寫成如同庫侖摩擦模型的式子:

式中,Q是摩擦力。庫侖摩擦模型是以實驗為基礎的,提供的是一個近似值,它對許多物理系統的分析給出了一個摩擦力的適當表示。摩擦因數μ是一個無量綱的標量值,它描述了兩個物體間摩擦力與對其施加的壓力的比值。摩擦因數的范圍從接近零到大于一 (例如,在較好的條件下,一個輪胎和混凝土的摩擦因數是1.7)。

3 實驗室摩擦力測量

用于實驗的設備是來自CMI設備公司的摩擦計,它的根據是“球盤式”技術。設備如圖3所示。它是由計算機控制的,能夠測量旋轉摩擦力和線性摩擦力。加熱單元允許的測量溫度是從室溫到150℃。更多的關于設備的詳細說明可以在CSM網站上得到。實驗計劃研究不同的參數,例如:

◇用不同性質的鉆井液來研究摩擦因數的差異;

◇用玄武巖、鋼鐵和混凝土做接觸面,因為它們與鉆桿經常接觸的面類似;

◇鉆桿常有比較高的井壁接觸力,使用不同的法向負荷來研究;

◇測量每一個潤滑劑不同溫度下的摩擦因數。

圖3 CMI設備公司的摩擦計

3.1 潤滑劑和測試樣品

實驗選取以下泥漿和潤滑劑:

◇水

◇水和蒙脫石

◇WD-40

◇油

◇油基WARP

◇Versavert

◇Glydril

◇Aphrons

選定的測試樣品在以下物質間測量摩擦力:

◇玄武巖

◇鋼鐵

◇混凝土

◇白堊

所有測試顯示了加入流體對摩擦力的重要影響。用不同流體在鋼鐵和鋼鐵間測量的摩擦因數如圖4所示。水的摩擦力最高而WARP的摩擦力最低。在這些測試中負荷的相關性較小。

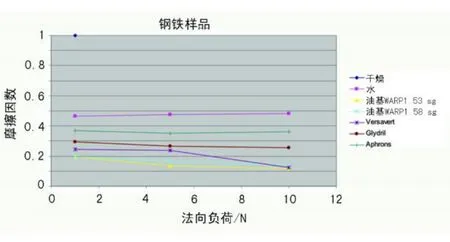
圖4 使用不同流體的鋼鐵和鋼鐵間的摩擦因數

其他類型的測試實例中的摩擦因數具有相同的趨勢。玄武巖的測試如圖5所示,與圖4比較,觀察到玄武巖的摩擦力比鋼鐵的高,這表明裸眼井眼的摩擦力比在套管內的高。

圖5 鋼鐵和玄武巖的摩擦因數

3.2 與溫度相關的摩擦力模型

人工扭矩和拖拽模型的說明不包括溫度影響。在實際應用中,對整個井或區分開的下套管井和裸眼井的摩擦因數進行反算。為了得到一個與測量數據好的擬合,有時必須使用不現實的摩擦因數。顯然,缺少現實的物理學會導致錯誤的結果。作為開發更準確的力學模型的第一步,需研究溫度影響。泥漿和接觸材料加熱的結果如圖6所示,從圖中可以清楚地觀察到摩擦因數隨溫度的增加而增加。可以看出,溫度從30℃增加到80℃時摩擦因數增加了20%～50%。最高的摩擦因數顯示了最高的溫度相關性。油基泥漿的摩擦因數較低,與溫度的關系很小。

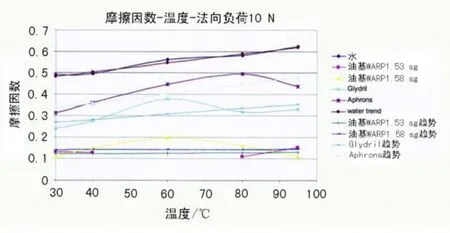
圖6 與溫度相關的摩擦因數

流體黏度隨溫度的增加而降低,黏度可能是解釋溫度影響的機理之一。假設一個線性趨勢直線,μ=a+bT,對不同流體與溫度的相關性的良好估計可由圖6來實現。得出的方程式如下:

水:μ=0.42+0.002 1·T

油基 (1.53 sg):μ=0.12+0.000 1·T

油基 (1.58 sg):μ=0.14+0.000 05·T

Glydril:μ=0.23+0.001 3·T

Aphrons:μ=0.27+0.002 2·T

4 溫度相關摩擦力的扭矩和拖拽模型

由于地層溫度隨深度的增加而增加,很明顯摩擦因數也是深度的函數。井底溫度隨深度經常是線性增加的,TZ=Tsurface+gTz,式中gT是地溫梯度。聯立溫度和摩擦因數的線性趨勢公式,可得:

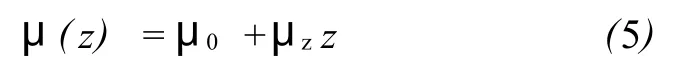
井中的溫度變化與圖6中的溫度范圍相似,因此可以把作為井深函數的摩擦因數公式化。在由Aadnoy和Djurhuus(2008年)建立的拖拽模型中應用了一個新的摩擦力模型μ(z)。由于微分方程結果的復雜性,僅僅建立了少數的解。然而,研究的目的是要得到所有幾何形態的一個詳盡的解析解。與Aadnoy和Djurhuus建立的廣義模型相比,一個顯著的差異就是實際垂直深度變成了一個顯式變量。為了推導出解析解,需要建立一些簡單的假定。首先,假設溫度是深度的線性函數,給定沿著傾斜面的拖拽力的方程式如下:

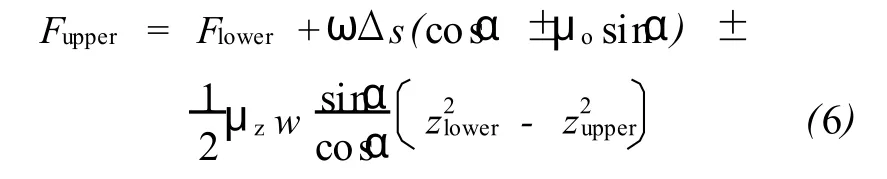
那么,ω為管柱的單位重力,N/m。

第二個假設是沿著一個單層構造或下降截面的摩擦因數變化不顯著,那么彎曲段的拖拽力如下:

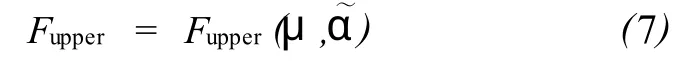
其中

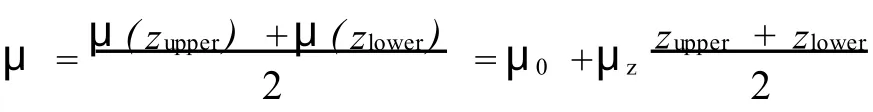
式中,是由Aadnoy和Djurhuus建立的拖拽力;是相應的角度定義。

4.1 實例

下面的例子把新的摩擦力模型應用于扭矩和拖拽模型,顯示了對井所產生的影響。輸入數據如表1:

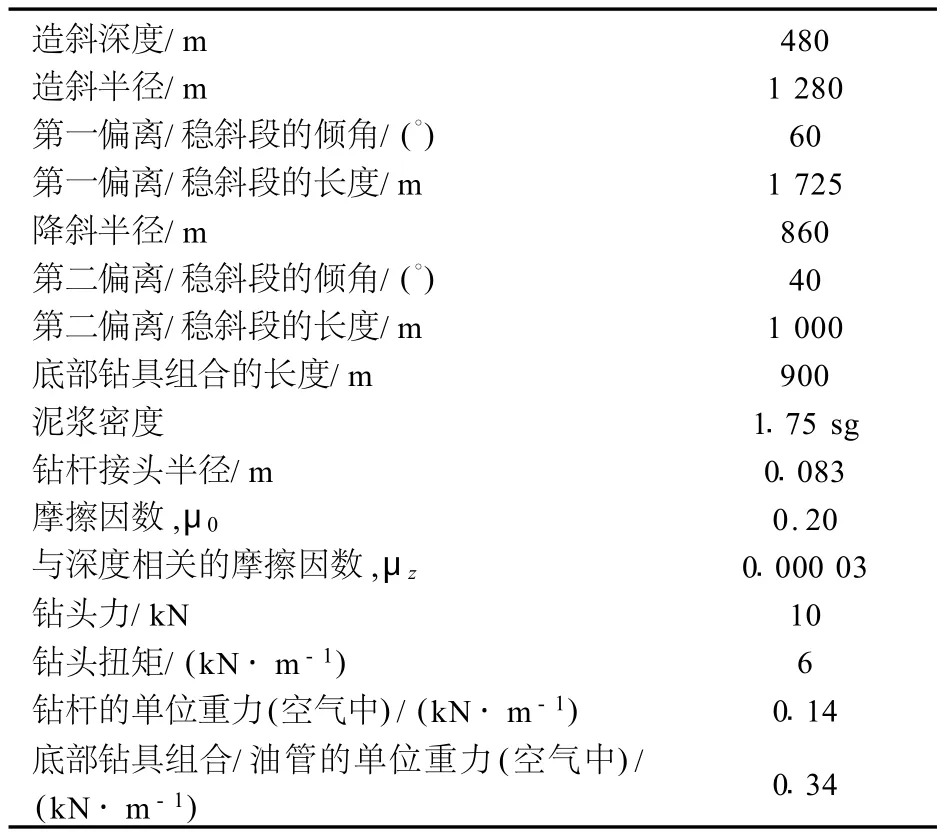
表1 阻力計算中的輸入數據

這口井是一個S形軌跡井,如圖7所示。

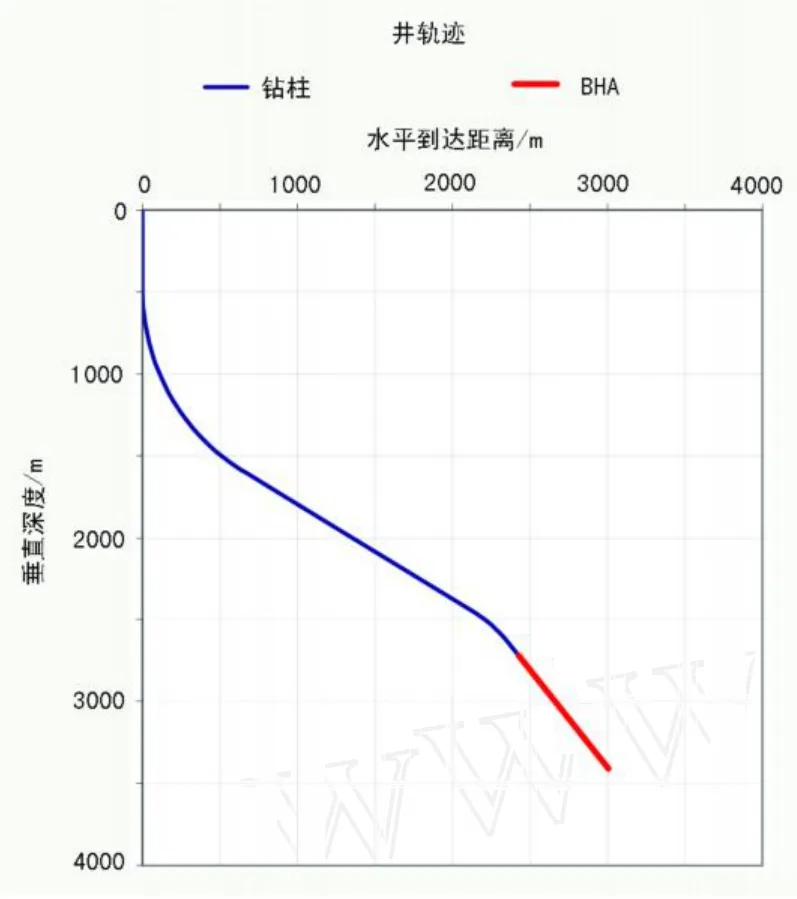
圖7 實例井的井軌跡

在圖8中顯示了牽引力和下降力。

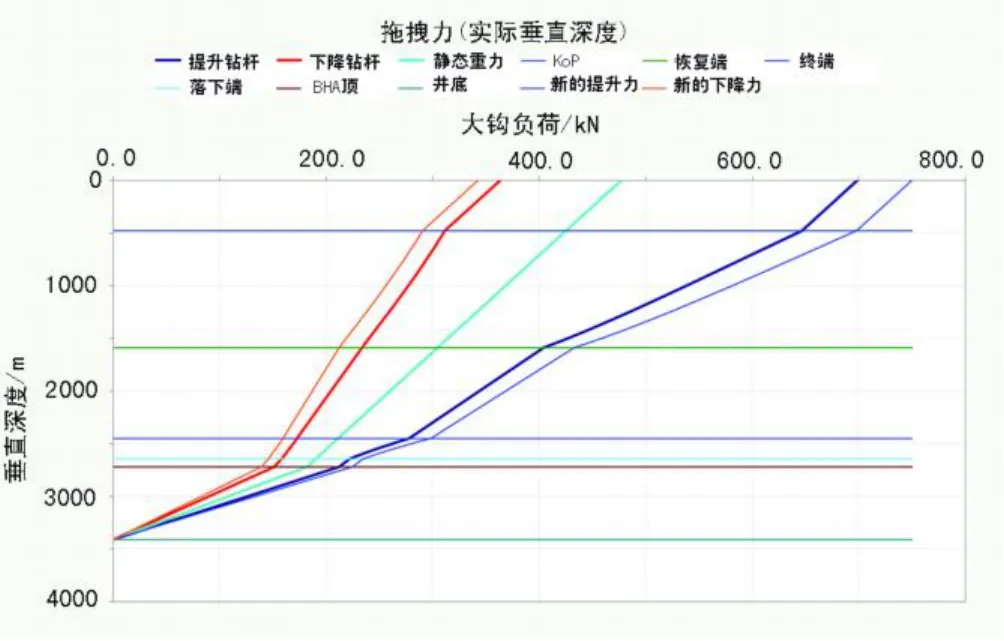
圖8 井的拽拖力對比

可以看出,通過使用與溫度相關的摩擦因數(從0.2增加到0.26)的牽引力與下降力都比摩擦因數為常數時計算的拖拽力變化顯著。使用高的摩擦因數來校正“舊”的模型,可以調整模型到測量的大鉤負荷。然而,這樣調整將僅僅修正表面值,而不能修正井底的力。在關鍵性操作中,如在水平井中安裝一個完井管柱時,知道局部的摩擦力是很重要的。

5 結論

呈現了在不同鉆井液與鋼鐵、混凝土與巖石之間的摩擦力的實驗數據,數據顯示:

◇摩擦因數取決于表面 (如鋼鐵與鋼鐵、鋼鐵與混凝土);

◇當溫度增加時摩擦因數通常增加。

呈現了與溫度相關的摩擦因數的模型,該模型聯立扭矩和拖拽模型,求解了許多簡單示例。

實例表明,如果使用與溫度相關的摩擦因數,拖拽力比使用當前工業模型計算的拖拽力高。這說明了與溫度相關的扭矩和拖拽模型在工業模擬器中的重要性。

資料來源于美國《SPE/IADC 119768》

10.3969/j.issn.1002-641X.2010.7.005

2009-03-28)