用非結(jié)構(gòu)化網(wǎng)格模擬器模擬聚合物驅(qū)

編譯:周長(zhǎng)江 (西南石油大學(xué)研究生部)

審校:施雷庭 (油氣藏地質(zhì)與開(kāi)發(fā)工程國(guó)家重點(diǎn)實(shí)驗(yàn)室·西南石油大學(xué))

用非結(jié)構(gòu)化網(wǎng)格模擬器模擬聚合物驅(qū)

編譯:周長(zhǎng)江 (西南石油大學(xué)研究生部)

審校:施雷庭 (油氣藏地質(zhì)與開(kāi)發(fā)工程國(guó)家重點(diǎn)實(shí)驗(yàn)室·西南石油大學(xué))

描述了用非結(jié)構(gòu)化網(wǎng)格模擬聚合物驅(qū)的研究進(jìn)展。聚合物驅(qū)模擬涉及到很多專(zhuān)業(yè)問(wèn)題:聚合物溶液黏度 (具有剪切稀釋或剪切增稠的特性)是聚合物濃度、剪切速率、礦化度和油藏溫度的函數(shù);聚合物的流度控制能力受近井地帶高速剪切的影響;聚合物的熱力學(xué)降解是聚合物濃度、礦化度和油藏溫度的函數(shù);聚合物的滯留會(huì)影響其流動(dòng)特征。除此之外,文中還提供了方程的數(shù)值解法及其應(yīng)用實(shí)例。

聚合物驅(qū) 模擬 非結(jié)構(gòu)化網(wǎng)格

1 引言

聚合物驅(qū)已經(jīng)在油田大規(guī)模應(yīng)用,其概念很簡(jiǎn)單,即在注入水中加入少量水溶性聚合物以增加注入水的黏度,實(shí)現(xiàn)有利的流度比,從而提高水驅(qū)效果;但是,其機(jī)理是很復(fù)雜的。聚合物溶液黏度受聚合物濃度、礦化度、溫度及剪切速率等因素的影響;吸附和滯留降低了聚合物濃度和水相滲透率;降解作用使聚合物喪失其增黏能力。因此,合理的聚合物驅(qū)設(shè)計(jì)和評(píng)價(jià)必須結(jié)合油藏特征、室內(nèi)實(shí)驗(yàn)、油藏模擬、工藝技術(shù)及礦場(chǎng)試驗(yàn)。其中,準(zhǔn)確的油藏模擬是聚合物驅(qū)設(shè)計(jì)和效果評(píng)價(jià)的關(guān)鍵。

從20世紀(jì)60年代后期開(kāi)始,很多學(xué)者進(jìn)行了聚合物驅(qū)數(shù)值模擬研究。1968年,Zeito提出了一個(gè)簡(jiǎn)單的聚合物驅(qū)數(shù)學(xué)模型:水相黏度是聚合物濃度的函數(shù)。1969年,Jewett和Shurz根據(jù)近60個(gè)聚合物驅(qū)項(xiàng)目,開(kāi)發(fā)了一個(gè)兩相、多層、能夠模擬一維介質(zhì)和五點(diǎn)井網(wǎng)的模擬器。1970年,Slater和Farouq Ali采用阻力系數(shù)經(jīng)驗(yàn)公式和差分方法模擬五點(diǎn)井網(wǎng)聚合物驅(qū)。Bondor和 Hirasaki(1972年)以及Hirasaki和Pope(1974年)開(kāi)發(fā)的數(shù)學(xué)模型認(rèn)為聚合物只溶于水中,他們用修正的Blake -Kozeny模型并考慮了聚合物吸附、滲透率下降系數(shù)和聚合物溶液非牛頓流變特性的影響。1976年,Vela、Peaceman和 Sandvik開(kāi)發(fā)的模擬器考慮了聚合物滯留、不可入孔隙體積、剪切降解和礦化度的影響。許多學(xué)者還考慮了化學(xué)降解和熱力學(xué)降解對(duì)聚合物溶液特性的影響。

20世紀(jì)80年代以來(lái),油藏模擬變得越來(lái)越復(fù)雜,對(duì)計(jì)算的準(zhǔn)確性要求也越來(lái)越高。通過(guò)對(duì)工藝技術(shù)和流線(xiàn)的研究,現(xiàn)代油藏模擬力求實(shí)現(xiàn)對(duì)細(xì)小裂縫、復(fù)雜井眼軌跡等多方面的影響因素進(jìn)行模擬。與常規(guī)網(wǎng)格系統(tǒng)相比,非結(jié)構(gòu)化網(wǎng)格系統(tǒng)能夠獲得更多、更準(zhǔn)確的地質(zhì)和工程信息。對(duì)常規(guī)網(wǎng)格系統(tǒng)的研究比較成熟,而關(guān)于非結(jié)構(gòu)化網(wǎng)格系統(tǒng)的研究卻較少。2001年,Beckner等人為ExxonMobil公司開(kāi)發(fā)了非結(jié)構(gòu)化網(wǎng)格模擬器,并對(duì)一個(gè)擁有復(fù)雜地質(zhì)裂縫和多個(gè)油藏、采用常規(guī)工藝技術(shù)生產(chǎn)的油田進(jìn)行了模擬。研究結(jié)果表明:大約10萬(wàn)個(gè)非結(jié)構(gòu)化網(wǎng)格就能實(shí)現(xiàn)相當(dāng)于160萬(wàn)個(gè)正交網(wǎng)格才能實(shí)現(xiàn)的地質(zhì)裂縫的準(zhǔn)確模擬,所以該模擬器簡(jiǎn)單易用,大大縮減了模擬時(shí)間。

常規(guī)油藏模擬的基本方程見(jiàn)附錄A(附錄見(jiàn)原文,下同)。這些方程中包括體積守恒方程和組分摩爾守恒方程。總體積守恒方程A-8用來(lái)求解壓力,各相體積守恒方程A-7用來(lái)求解相飽和度,摩爾守恒方程A-18用來(lái)求解各組分摩爾數(shù)。

2 聚合物驅(qū)的物理模型

正如引言中提到的那樣,聚合物驅(qū)機(jī)理是非常復(fù)雜的。EMpower是 ExxonMobil公司在MARS模擬器基礎(chǔ)上開(kāi)發(fā)的新型模擬器。其特點(diǎn)包括:用非結(jié)構(gòu)化網(wǎng)格模擬聚合物驅(qū);聚合物溶液性質(zhì)與礦化度、剪切增稠和聚合物降解等因素有關(guān)。該模擬器結(jié)合油藏中流體的流動(dòng)、布井方式、流線(xiàn)和工藝技術(shù),能夠準(zhǔn)確有效地模擬復(fù)雜油藏。

2.1 聚合物溶液黏度

聚合物溶液是非牛頓流體,在低剪切速率下,黏度隨剪切速率的增加而降低。但是,一些學(xué)者已經(jīng)證明了聚合物溶液在多孔介質(zhì)中具有明顯的剪切增稠特性。2008年,Delshad等人證明了剪切增稠是德布拉數(shù)的函數(shù)。EMpower既能模擬聚合物的剪切稀釋,又能模擬剪切增稠。除剪切速率外,聚合物溶液黏度還是聚合物濃度、礦化度和溫度的函數(shù)。

2.2 傳導(dǎo)率修正

通常,近井地帶的剪切速率高于油藏中的剪切速率。因此,從井底到油藏中剪切速率的變化需要特殊處理,尤其是當(dāng)井眼位于大網(wǎng)格塊中時(shí)。在本文的研究過(guò)程中,根據(jù)近井地帶剪切速率的變化對(duì)傳導(dǎo)率進(jìn)行修正,這可以通過(guò)模擬井眼周?chē)鷫航祵?duì)黏度的影響來(lái)實(shí)現(xiàn)。

2.3 不可入孔隙體積

不可入孔隙體積 (IPV)描述了聚合物不能進(jìn)入的孔隙空間。IPV可理解為:孔壁排斥效應(yīng)和孔喉排斥效應(yīng)。在孔壁排斥效應(yīng)中,聚合物溶液流經(jīng)所有孔隙,但聚合物集中在高速區(qū)而遠(yuǎn)離孔隙表面。在孔喉排斥效應(yīng)中,聚合物只流經(jīng)大孔隙 (含一部分中孔隙)而不流經(jīng)小孔隙。在 EMpower中,考慮到IPV的影響,對(duì)聚合物的流速進(jìn)行了調(diào)整。IPV與巖石類(lèi)型和滲透率有關(guān)。

2.4 聚合物吸附

吸附和滯留是聚合物在多孔介質(zhì)中損失的主要原因,與滲透率 (代替孔隙表面積)有關(guān)。EMpower可將聚合物吸附分為可逆和不可逆兩種情況進(jìn)行模擬。

2.5 殘余阻力系數(shù) (RRF)

聚合物吸附可引起孔隙縮小,從而降低水相滲透率。水相滲透率下降是聚合物吸附量的函數(shù)。通常,殘余阻力系數(shù)只降低水相滲透率,幾乎不影響油相滲透率。

2.6 聚合物降解

聚合物不僅會(huì)發(fā)生熱力學(xué)降解,還會(huì)與地層水中的金屬陽(yáng)離子反應(yīng)而沉降。不同的油田,對(duì)聚合物耐鹽性有不同的要求。本文在模擬聚合物降解時(shí)考慮了溫度和各種金屬陽(yáng)離子的影響。

3 數(shù)學(xué)方程

模擬時(shí)間步的目的是為了獲得在該時(shí)間步結(jié)束時(shí)的壓力、組分?jǐn)?shù)量及相飽和度,可根據(jù)巖石和流體的性質(zhì)獲得這些參數(shù)的初始值。文中建立了多個(gè)數(shù)學(xué)方程,通過(guò)IMPES、耦合-隱含、順序及IMPSAT算法來(lái)求解這些未知數(shù)。在解出壓力、飽和度及其他組分的摩爾數(shù)之后,再求解聚合物的摩爾數(shù)。方程的選擇需要綜合考慮穩(wěn)定性和計(jì)算機(jī)的運(yùn)算能力。

根據(jù)體積守恒方程A-8可推導(dǎo)出求解壓力變化的線(xiàn)性方程。線(xiàn)性方程A-15的算法決定了求解組分摩爾流量的復(fù)雜程度。

3.1 IMPES算法

對(duì)于IMPES和順序算法,壓力方程如式 (1)所示:

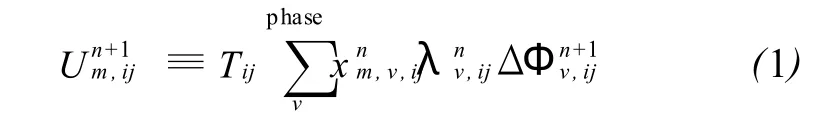
由于其穩(wěn)定性差使用得較少。在IMPES算法中,壓力隨時(shí)間變化,而飽和度是固定不變的。當(dāng)流速較高、前緣飽和度變化較快的時(shí)候,不能很好地模擬油藏實(shí)際情況。

3.2 耦合-隱含算法

1980年,Coats提出了耦合-隱含 (CI)算法,可同時(shí)準(zhǔn)確求解壓力和組分摩爾數(shù)。與IMPES算法相比,它更穩(wěn)定,但運(yùn)算速度較慢。CI算法的組分流動(dòng)方程如下所示:

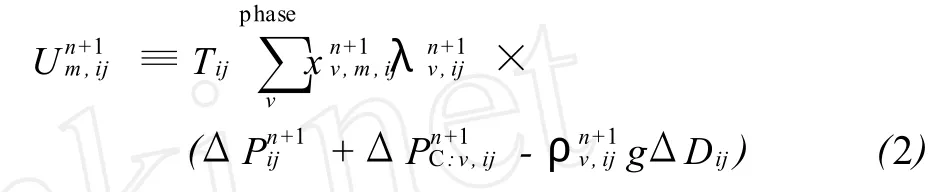
組分的摩爾守恒方程見(jiàn)A-15。對(duì)式 (2)相飽和度求導(dǎo) (因?yàn)榉匠讨酗柡投仁且蜃兞?便可得相體積守恒方程A-7。體積守恒方程A-8用來(lái)求解壓力。

3.3 順序算法

1973年,Spillette、Hillestad和Stone提出了一種介于IMPES算法和CI算法之間的順序算法。1986年,Watts用同樣的方法建立了組分模型。與CI算法同時(shí)求解壓力和摩爾數(shù)不同,順序算法是先求解壓力,然后依次求解飽和度和摩爾數(shù)。首先,用順序算法將壓力方程線(xiàn)性化以求解壓力變化;然后將飽和度方程線(xiàn)性化,求出飽和度變化;再將組分的摩爾守恒方程A-15線(xiàn)性化,便可計(jì)算組分?jǐn)?shù)變化;最后,根據(jù)最新的組成計(jì)算下一時(shí)間步的飽和度。

3.4 IMPSAT算法

1989年,Quandalle和Savary首次提出了IMPSAT算法,稱(chēng)之為隱式壓力、隱式飽和度算法。1999年,Cao和Aziz在傳導(dǎo)方程中顯式計(jì)算相密度和組分的摩爾分?jǐn)?shù),研究表明,壓力與組分摩爾分?jǐn)?shù)之間的相關(guān)度要比壓力與相飽和度之間的相關(guān)度弱。根據(jù)定義,IMPSAT算法同時(shí)隱式求解壓力和飽和度,而顯式求解組分摩爾分?jǐn)?shù),因此,它相似于但又不同于分兩步求解壓力和飽和度的順序算法。在這幾種算法中,隱式程度由低到高的順序?yàn)镮MPES、順序、IMPSA T、CI。與之對(duì)應(yīng),IMPSAT算法在運(yùn)算上的穩(wěn)定性比IMPES算法和順序算法要好,但比CI算法差。因?yàn)镮MPSA T算法每個(gè)節(jié)點(diǎn)可以求解3個(gè)未知數(shù),所以比IMPES算法 (每個(gè)節(jié)點(diǎn)求解1個(gè)未知數(shù))和順序算法 (每個(gè)節(jié)點(diǎn)求解1+2個(gè)未知數(shù))的運(yùn)算成本高,但與全隱式算法相比,對(duì)計(jì)算機(jī)內(nèi)存和CPU的要求相對(duì)較低。

4 聚合物摩爾守恒

為模擬聚合物驅(qū)油過(guò)程,還需增加聚合物和鹽的摩爾守恒方程。式 (3)所列方程包含水相中溶解的聚合物、巖石表面吸附的聚合物、降解損失以及水相中作為示蹤劑的聚合物的量。該方程包括黏度和吸附對(duì)水相流度的影響以及IPV對(duì)聚合物流速的影響。

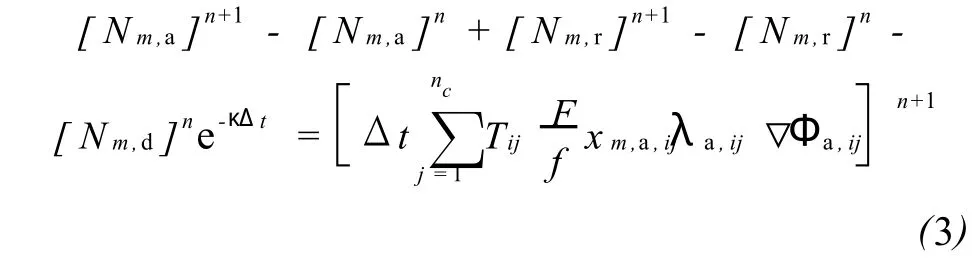
式中 m——聚合物組分;

a——水相;

r——巖石;

d——降解后的聚合物;

κ——熱降解常數(shù);

Nm,a——溶解聚合物的摩爾數(shù);

Nm,r——巖石表面吸附的聚合物摩爾數(shù);

Nm,d——降解的聚合物摩爾數(shù);

F——模擬低滲透巖石對(duì)聚合物的“封堵”系數(shù);

f——不可入孔隙體積的函數(shù)。上式可簡(jiǎn)化為:

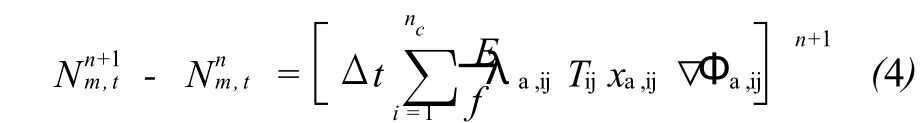
式中,t表示聚合物總摩爾數(shù)。在每個(gè)網(wǎng)格中,將聚合物吸附和降解看作點(diǎn)源和點(diǎn)匯。顯式算法中,在時(shí)間步開(kāi)始時(shí)求解這些參數(shù)并假設(shè)其在時(shí)間步長(zhǎng)中保持為常數(shù)。降解常數(shù)κ由用戶(hù)自定義。先計(jì)算降解再計(jì)算吸附。吸附是水相中聚合物濃度的函數(shù),并符合Langmuir等溫吸附。殘余阻力系數(shù)是聚合物在巖石表面吸附量的函數(shù),反映了該網(wǎng)格聚合物的吸附量和降低水相滲透率的能力。獲得吸附降解后的聚合物濃度,便可計(jì)算水相黏度,從而通過(guò)方程 A-4可計(jì)算相流度。通常,f=1.0-IPV (IPV由用戶(hù)自定義),并存在區(qū)域性變化。F是模擬低滲透巖石對(duì)聚合物的“封堵”系數(shù),是網(wǎng)格滲透率的函數(shù)。雖然聚合物摩爾數(shù)可通過(guò)顯式或隱式求解,但還是應(yīng)根據(jù)穩(wěn)定性來(lái)決定采用哪種方式求解。假設(shè)水相密度不受聚合物濃度的影響。

5 模擬結(jié)果

5.1 模擬巖心驅(qū)替實(shí)驗(yàn)

將EMpower模擬聚合物驅(qū)的采收率情況與Masuda等人1992年的巖心驅(qū)替實(shí)驗(yàn)結(jié)果進(jìn)行比較。Masuda等人測(cè)量了 HPAM溶液在玻璃微珠人造多孔介質(zhì)模型中的流變性 (圖1),并通過(guò)巖心驅(qū)替實(shí)驗(yàn)測(cè)量了聚合物驅(qū)采收率提高幅度。在不調(diào)整模型參數(shù)的情況下,EMpower模擬結(jié)果與實(shí)驗(yàn)結(jié)果的擬合度較高。實(shí)驗(yàn)和模擬結(jié)果如圖2和圖3所示。

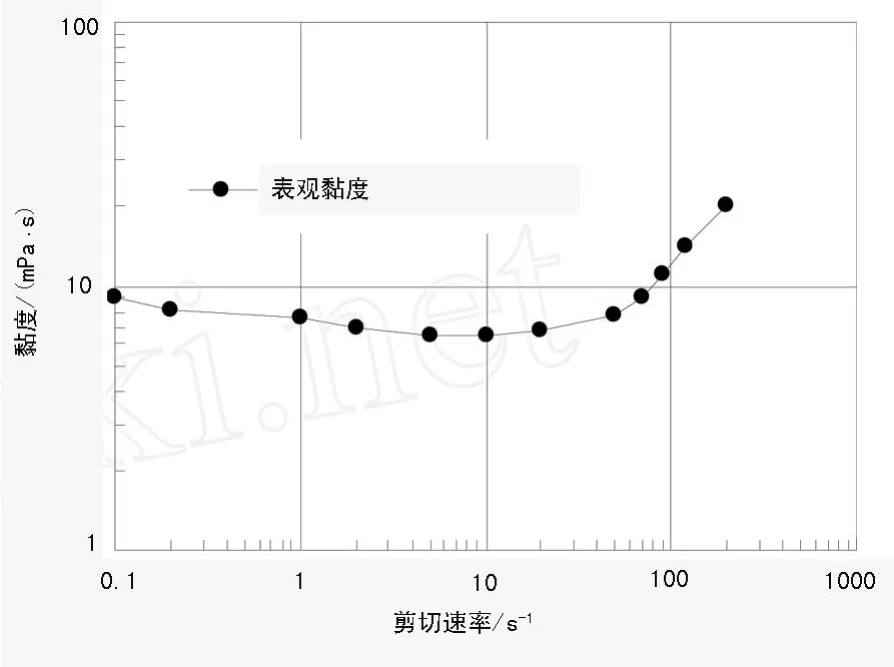
圖1 HPAM溶液 (200 ppm)的流變曲線(xiàn)

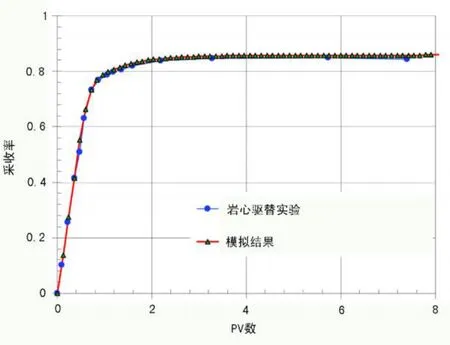
圖2 采收率隨注入PV數(shù)的變化曲線(xiàn)

5.2 非結(jié)構(gòu)化網(wǎng)格模型

2001年,Beckner等人為 ExxonMobil公司開(kāi)發(fā)了非結(jié)構(gòu)化網(wǎng)格模擬器 EMpower。對(duì)復(fù)雜結(jié)構(gòu)井(如大斜度井、水平井和多分支井)、斷層和尖滅進(jìn)行網(wǎng)格劃分是比較復(fù)雜的,但使用非結(jié)構(gòu)化網(wǎng)格就比較簡(jiǎn)單。

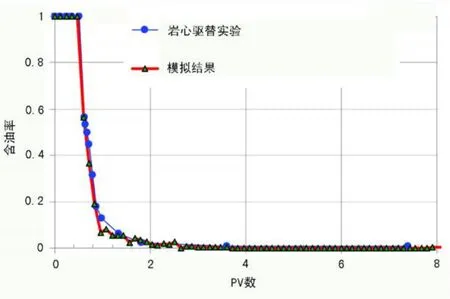
圖3 含油率隨注入PV數(shù)的變化曲線(xiàn)

圖4 五點(diǎn)井網(wǎng)非結(jié)構(gòu)化網(wǎng)格示意圖

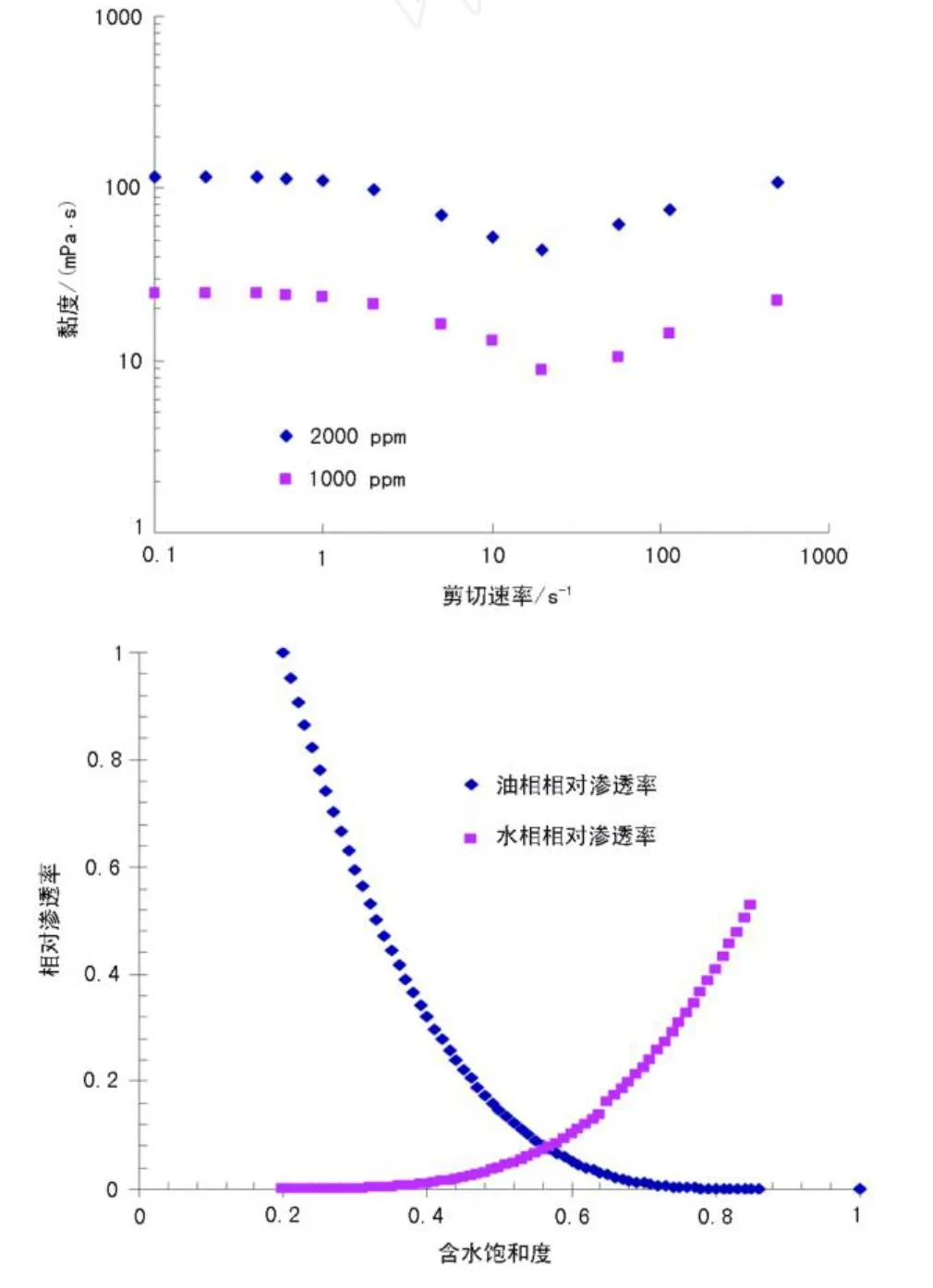
圖5 巖石和流體性質(zhì)

非結(jié)構(gòu)化網(wǎng)格允許使用多種網(wǎng)格技術(shù)對(duì)五點(diǎn)井網(wǎng)模型進(jìn)行模擬 (圖4)。網(wǎng)格結(jié)構(gòu)對(duì)聚合物驅(qū)效果影響很大,而非結(jié)構(gòu)化網(wǎng)格就降低了這樣的影響。當(dāng)聚合物溶液黏度低于油相黏度 (如聚合物驅(qū)替稠油)或者高黏聚合物驅(qū)轉(zhuǎn)后續(xù)水驅(qū)時(shí),容易發(fā)生黏性指進(jìn),應(yīng)特別注意網(wǎng)格的方位敏感性。五點(diǎn)井網(wǎng)模型聚合物驅(qū)實(shí)例的網(wǎng)格結(jié)構(gòu)如圖4(a)所示。模型尺寸為500 ft×50 ft×50 ft(1 ft=30.48 cm)。聚合物溶液的流變性如圖5所示。聚合物遵循Langmuir等溫吸附,最大吸附量為20μg/g砂。IPV為0.2。水相滲透率下降了20%,但油相滲透率不受影響。模型孔隙度為26%,滲透率為2 D。油水相對(duì)滲透率曲線(xiàn)如圖5所示。油藏初始含水飽和度為束縛水飽和度,初始?jí)毫? 140 psia(1 psi=6.895 kPa)。為了簡(jiǎn)化,不考慮礦化度、聚合物降解和油水壓縮性的影響 (體積系數(shù)為1),并且只模擬二維的情況。聚合物注入濃度為1 500 ppm(1 ppm=10-6),注聚時(shí)間為10年。產(chǎn)油井井底壓力為1 500 psia。五點(diǎn)井網(wǎng)模型復(fù)雜非結(jié)構(gòu)化網(wǎng)格中含油飽和度和聚合物濃度如圖6所示。目前已開(kāi)展針對(duì)實(shí)際地質(zhì)模型的模擬,運(yùn)算速度較快。

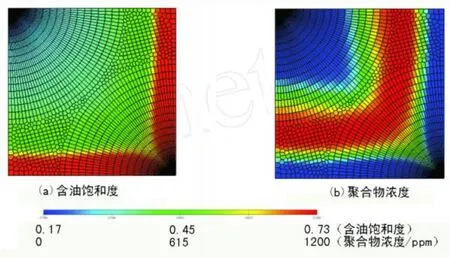
圖6 注聚5 730天后的含油飽和度和聚合物濃度分布

6 結(jié)論

非結(jié)構(gòu)化網(wǎng)格可以詳細(xì)地模擬聚合物驅(qū)過(guò)程,并有效地模擬復(fù)雜油藏。

聚合物驅(qū)模擬包括聚合物的流動(dòng)特性和驅(qū)替效果,其驅(qū)替特征如下:

◇聚合物溶液黏度是聚合物濃度、剪切速率、礦化度和油藏溫度的函數(shù);

◇聚合物溶液黏度具有剪切稀釋或剪切增稠的特性;

◇傳導(dǎo)系數(shù)受近井地帶高速剪切的影響;

◇聚合物降解是聚合物濃度、離子濃度和油藏溫度的函數(shù);

◇聚合物滯留對(duì)聚合物流動(dòng)特性有重要影響;

◇可使用多種數(shù)值算法 (如順序算法,IMPSAT等)和多種模型 (如黑油模型、組分模型和熱采模型)進(jìn)行聚合物驅(qū)模擬。

資料來(lái)源于美國(guó)《SPE 118985》

10.3969/j.issn.1002-641X.2010.7.001

2009-04-08)