線性相依條件下未確知機(jī)會(huì)約束規(guī)劃的解法
李小青,周長(zhǎng)銀,王延朝
(山東科技大學(xué)信息科學(xué)與工程學(xué)院,山東青島 266510)
線性相依條件下未確知機(jī)會(huì)約束規(guī)劃的解法
李小青,周長(zhǎng)銀,王延朝
(山東科技大學(xué)信息科學(xué)與工程學(xué)院,山東青島 266510)
在未確知數(shù)為線性相依條件下,研究了一般線性約束形式的未確知機(jī)會(huì)約束規(guī)劃問(wèn)題的解法,并給出具體算例說(shuō)明了該方法的可行性。同時(shí),這種處理問(wèn)題的思想對(duì)建立未確知支持向量機(jī)也有很大的現(xiàn)實(shí)意義。
未確知有理數(shù);線性相依;可信度;機(jī)會(huì)約束規(guī)劃
0 引言
目前對(duì)確定性信息的研究已形成了一套比較完整的理論體系。然而,在實(shí)際工作和生活中卻存在著大量的不確定性信息,大體上可以分為隨機(jī)信息、模糊信息、灰信息和未確知信息[1]。未確知信息是一種不同于以上三種信息的另一種信息,它最早由中國(guó)工程院院士王光遠(yuǎn)教授提出[2]。這種信息的不確定性是由于決策者不能完全把握事物的真實(shí)狀態(tài)和數(shù)量關(guān)系而造成的純主觀認(rèn)識(shí)上的不確定性。隨著人們對(duì)未確知信息的不斷深入研究,目前已初步形成了一套未確知信息理論,并在未確知有理數(shù)理論的基礎(chǔ)上構(gòu)造了未確知機(jī)會(huì)約束規(guī)劃問(wèn)題。但目前只解決了未確知機(jī)會(huì)約束規(guī)劃中當(dāng)約束條件為g(x,B)=B-h(x),g(x,B)=h(x)-B這兩種形式的規(guī)劃問(wèn)題的算法[3],筆者要討論的約束條件為更一般的線性形式:g(x,B)=h(x)A-B的未確知機(jī)會(huì)約束規(guī)劃模型。利用線性相依未確知有理數(shù)的相關(guān)理論,在未確知數(shù)A, B滿足線性相依條件下,給出了未確知機(jī)會(huì)約束規(guī)劃的一個(gè)解法。
1 未確知數(shù)理論
定義1[4]對(duì)任意閉區(qū)間[a,b],a=x1<… 定義2[5]設(shè) A=[[x1,xn],f(x)]和 B=[[y1,yn], g(y)]為同階未確知有理數(shù),其中 若當(dāng)確信A取xi時(shí),B取yi,且當(dāng)B取yi時(shí),A取xi,則稱A和B是相依未確知有理數(shù)。 定義3[5]設(shè)A與B為相依未確知有理數(shù),當(dāng)且僅當(dāng)αi=βi,(i=1,2,…,n)時(shí),則稱 A與B是線性相依的。 定義4[5]設(shè)A與B是相依的未確知有理數(shù),稱同階未確知有理數(shù)C=[[x1+y1,xn+yn],h(z)]為相依未確知有理數(shù)A與B的和,記作C=A?B,其中 由以上定義知,任意的未確知有理數(shù)A與它自身是線性相依的,同時(shí),若把實(shí)數(shù)a定義為未確知有理數(shù)的形式,則未確知有理數(shù)與實(shí)數(shù)也是線性相依的。 定理1[5]設(shè)G為所有與某一n階未確知有理數(shù)線性相依的n階未確知有理數(shù)的非空集合,則按上述的加法和數(shù)乘運(yùn)算,G是實(shí)數(shù)域R上的線性空間。 定理2設(shè)k∈R為任意常數(shù),A為實(shí)數(shù),未確知有理數(shù)B具有定義2中的形式,則未確知事件的可信度Cr{k(A-B)≤0}等價(jià)于下面兩種形式:當(dāng)k>0時(shí),Cr{k(A-B)≤0}=Cr{AB≤0};當(dāng)k<0時(shí),Cr{k(A-B)≤0}=Cr{A-B≥0}。 證明由未確知有理數(shù) B的形式可知:kB=[ky1, kyn],g′(y)],其中 考慮如下的未確知機(jī)會(huì)約束規(guī)劃問(wèn)題: 其中x∈Rn為決策向量,Bi(i=1,2,…,p)為未確知參數(shù)向量。f(x)為不含未確知參數(shù)的目標(biāo)函數(shù),g(x,Bi),i=1,2,…,p為約束函數(shù),α∈[σ,1]為事先給定的置信水平,Cr{.}為未確知事件的可信度。 對(duì)于未確知機(jī)會(huì)約束規(guī)劃,當(dāng)約束函數(shù)為特殊情形,即g(x,B)=B-h(x),g(x,B)=h(x)-B時(shí),利用文獻(xiàn)[3]中的算法,將未確知約束條件轉(zhuǎn)化為相應(yīng)的確知等價(jià)類,從而可將整個(gè)未確知規(guī)劃問(wèn)題轉(zhuǎn)化為一個(gè)確知問(wèn)題,再利用確知規(guī)劃的方法解之。下面我們考慮當(dāng)約束條件為一般形式時(shí),即 g(x,Bi)=h(x)A-Bi(其中h(x)為決策變量 x的函數(shù), A,Bi(i=1,2,…,p)為未確知有理數(shù)),當(dāng)A與Bi(i=1,2,…,p)為線性相依未確知有理數(shù)時(shí),未確知機(jī)會(huì)約束規(guī)劃問(wèn)題的解法。 設(shè)A=[[x1,xn],f(x)]與Bi(i=1,2,…,p)為線性相依未確知有理數(shù),其中 設(shè)Bi=A+ai,Bi=[[x1+ai,xn+ai],wi(y)],其中 其中ai∈R為任意的實(shí)數(shù)。 根據(jù)第二部分的線性相依理論,我們考慮線性相依條件下未確知機(jī)會(huì)約束規(guī)劃中當(dāng)約束條件為一般形式時(shí)的解法。 g(x,Bi)=h(x)A-Bi=h(x)A-(A+ai)=h(x)AA-ai=[h(x)-1]A-ai。 利用曲線 h(x)-1可以把整個(gè)空間劃分為3部分,即h(x)-1>0,h(x)-1<0,h(x)-1=0。 對(duì)于 h(x)-1≠0,則有 相應(yīng)的未確知機(jī)會(huì)約束規(guī)劃中的條件 Cr{g(x,Bi)≤0}≥α,即可寫成如下形式 利用上面的定理2可知(1)式等價(jià)于以下兩種形式: ,則上面兩個(gè)式子可表示成如下形式: 于是,對(duì)于一般形式的約束條件g(x,Bi)=h(x)A-Bi就轉(zhuǎn)化為目前已解決的g(x,B)=B-h(x),g(x,B)=h(x)-B的形式,接著利用文獻(xiàn)[3]中的算法,可將約束條件為一般形式的未確知機(jī)會(huì)約束規(guī)劃轉(zhuǎn)化為與其等價(jià)的確知規(guī)劃。 特別的,對(duì)于h(x)-1=0的情形,未確知約束條件就簡(jiǎn)化為Cr{-ai≤0}≥α的形式,因此,若 ai<0,則無(wú)解;若ai≥0,則未確知約束條件就等價(jià)為 h(x)-1=0。 對(duì)于上述線性相依條件下的未確知機(jī)會(huì)約束規(guī)劃問(wèn)題的解法,我們給出一個(gè)具體算例。 解如下的未確知機(jī)會(huì)約束規(guī)劃: 設(shè)未確知有理數(shù)A=[[1,4],f(x)],B=A+2=[[3,6], w(x)],其中 記h(x)=3x1+x2,而A與B為線性相依未確知有理數(shù),顯然該規(guī)劃的約束條件具有g(shù)(x,B)=h(x)A-B的一般形式。利用第三部分所給的方法解此規(guī)劃問(wèn)題,步驟如下:當(dāng)h(x)-1≠0時(shí),可將規(guī)劃(2)中的未確知約束條件Cr{(3x1+x2)A-B≤0}≥0.8轉(zhuǎn)化為下面的等價(jià)問(wèn)題: 這樣就把約束條件為一般形式的未確知問(wèn)題轉(zhuǎn)化為目前已解決的約束條件為特殊形式的問(wèn)題,接著再利用文獻(xiàn)[3]中的算法就可求得整個(gè)問(wèn)題的解。步驟如下。 首先,將未確知有理數(shù)A表示成其分布型: 再根據(jù)文獻(xiàn)[3]中的算法,將式(3),式(4)中的兩個(gè)式子轉(zhuǎn)化為其相應(yīng)的確知等價(jià)類: 于是,當(dāng) h(x)-1≠0時(shí),原未確知機(jī)會(huì)約束規(guī)劃(2)的確知規(guī)劃為: 特殊情形時(shí),即當(dāng)3x1+x2-1=0時(shí),并且這里的a= 2>0,則原問(wèn)題(2)等價(jià)于下面的規(guī)劃 筆者研究了在兩未確知有理數(shù)為線性相依條件下未確知機(jī)會(huì)約束規(guī)劃問(wèn)題的解法,對(duì)于建立未確知支持向量機(jī)的設(shè)想具有一定的現(xiàn)實(shí)意義,但對(duì)于一般情況下的解法還需進(jìn)一步研究。 [1] Yang Zhimin.Review of the monograph mathematical treatment and application of uncertain information[J]. Chinese Science Bulletion,2001(7):615-616. [2] 王光遠(yuǎn).未確知信息及其數(shù)學(xué)處理[J].哈爾濱建筑工程學(xué)院學(xué)報(bào),1999(4):1-4. [3] 楊志民,鄧乃揚(yáng).未確知機(jī)會(huì)約束規(guī)劃[J].系統(tǒng)工程, 2004:11-14. [4] 楊志民,劉廣利.不確定性支持向量機(jī)原理及應(yīng)用[M].北京:科學(xué)出版社,2007:38-202. [5] 高志強(qiáng),王義鬧.相依未確知信息的數(shù)學(xué)表達(dá)及其運(yùn)算[J].華中科技大學(xué)學(xué)報(bào),2003(4):36-38. [6] Charens A,Cooper W.Chance constrained programming [J].Management Science,1959(1). [7] András Prékopa.On probabilistic constrained programming [M].Princeton:Princeton university press,1970:113 138. (責(zé)任編校:夏玉玲) The Method of Unascertained Chance Constrained Programming under the Conditions of Linear Interdependence LI Xiao-qing,ZHOU Chang-yin,WANG Yan-zhao Under the linear interdependence condition,the solution is studied about unascertained chance constrained programming with general linear constrain and method for solving the problem is proposed with numerical examples to demonstrate the method’s feasibility.Such a way to deal with problems has great practical significance for the establishment of unascertained support vector machines. unascertained rational number;linear interdependence;credible degree;chance con-strained programming O211.5 A 1672-349X(2010)06-0010-03 2010-06-02 國(guó)家自然科學(xué)基金項(xiàng)目(10971122);山東省自然科學(xué)基金項(xiàng)目(Y2008A 01) 李小青(1983-),女,碩士研究生,主要從事隨機(jī)優(yōu)化及未確知支持向量機(jī)研究。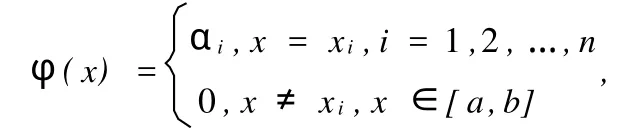




2 線性相依條件下未確知機(jī)會(huì)約束規(guī)劃問(wèn)題的解法







3 算例








4 結(jié)束語(yǔ)
(College of Information Science and Engineering,SUST,Qingdao 266510,China)

