淺談《線性代數》教學改革與實踐

邵紅梅

（廊坊武警學院 基礎部，河北 廊坊 065000）

淺談《線性代數》教學改革與實踐

邵紅梅

（廊坊武警學院 基礎部，河北 廊坊 065000）

結合《線性代數》課程本身的特點和學生的實際情況,通過對線性代數課程的教學實踐,從三個方面闡述了如何提高線性代數的教學效果.

線性代數；形象化；具體化；聯系；思維能力

線性代數課程在高等工科學校的教學計劃中是一門基礎理論課，也是研究生入學考試的一門必考課程.這門課程是中學代數的繼續和提高，它的思想和方法如今已經滲透到數學的各個領域中.而且隨著計算機的快速發展，用代數方法解決實際問題已滲透到現代科學、技術、經濟、管理的各個領域，尤其在計算機、通訊、電子等學科領域其重要性和實用性日漸顯現.但線性代數課程也同時存在著概念多、定理多，內容抽象的特點，使得學生在學習時普遍感到抽象、枯燥，缺乏主動學習的積極性，也造成了學生數學應用意識的淡薄.如何上好線性代數課，如何提高線性代數的課堂教學效果，一直受到人們的關注.下面結合自己的教學，通過多年的教學實踐，對這門課程的教學進行了改革，收到了很好的效果.主要作了以下幾方面的努力和嘗試：

1 將抽象的概念具體化、形象化

線性代數一般繼一年的微積分課程后開設，此時學生已初步具備高等數學的思維能力.但線性代數的概念一般都比較抽象，大多學生會感到無從入手，適當將抽象的概念具體化，形象化，從他們熟悉的知識或例子入手，可以提高學生的學習興趣，加深其對基本概念的理解.例如在學習n階行列式的概念時，對于n階行列式的含義，學生會感到很抽象，產生畏難情緒.針對這種情況，以學生在中學數學中學過的解二元線性方程組為例引出二階行列式的定義，則使學生感到輕松易學.然后提出三階行列式如何定義的問題，讓學生參與該定義的過程，學生很快會給出三階行列式的定義，在這種氛圍下，再逐步引出四階、五階直至n階行列式的定義，這樣學生就較容易掌握n階行列式的概念;再例如，在講解矩陣的運算時，可以利用常用的數的四則運算來推導矩陣的四則運算，矩陣的加法減法運算可以舉例為特定人群的工資表作為一個矩陣的同時加薪和減薪問題，然后介紹矩陣的乘法，學生很自然會思考一個數表和另一個數表相乘會遵循什么規則，在給出乘法規則后，學生感覺很難理解，甚至提出為什么不能像矩陣與矩陣的加法那樣規定，然后教師舉出一例來說明矩陣乘法的用途.例如，設有n個未知數m個方程式的線性方程組:

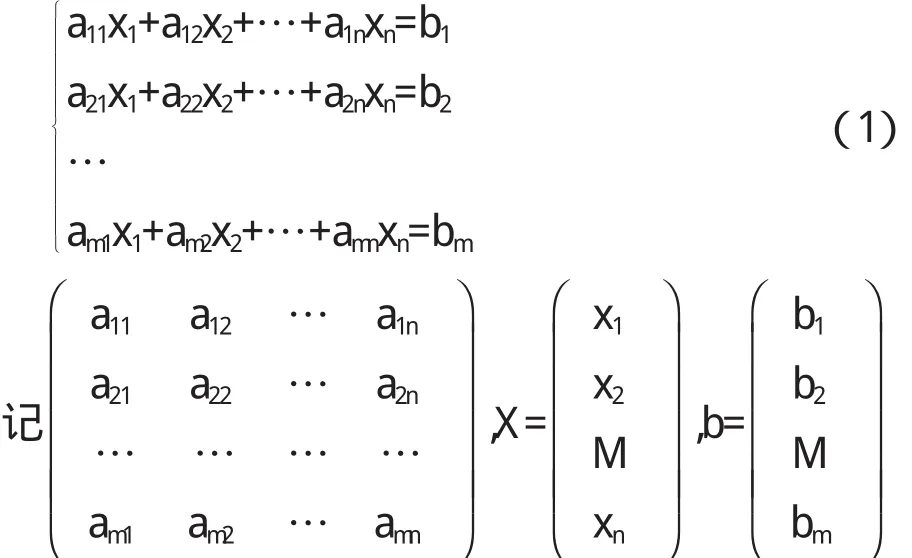
學生們不難自己求出A X，它正好就是b，即A X=b(2).這學生既看到了矩陣乘積的應用，又加深了對該法則的理解，更重要的是它可以使我們可以想象是否可以用矩陣的某些運算來處理線性方程組.通過類似問題的提出，增強了學生探索問題的興趣，培養了創新意識和素質.

2 串聯內容，注意聯系

線性代數各章節的內容，不是孤立割裂的，而是相互滲透、緊密聯系的，所以教師在授課過程中應注意各章節內容之間的聯系，尤其是對各個概念的等價條件，一定要引導學生去總結發現，這樣既使學生不會產生概念混淆，條理混亂，又鍛煉了學生的邏輯思維能力.如A是n階方陣，若:|A|≠0(稱A為非奇異陣)則以下命題等價：

（1）存在若干個初等陣P1，P2，…，Pn，使得PnPn-1…P1A+E；

（2）A可以經過有限次初等行變換化為單位矩陣；

（3）A是可逆陣；

（4）存在n階方陣B，使得A B=B A=E；

（5）r(A)=n(稱A是滿秩)；

（6）A可表示為若干個可逆陣的乘積；

（7）A可表示成若干個初等陣的積；

（8）A的列向量組線性無關(列滿秩)；

（9）A的行向量組線性無關(行滿秩).

再例如，線性代數的核心問題就是“線性方程組”問題，由此引出矩陣和向量的概念.歷年來，學生對“向量組線性相關性”的問題都不能透徹地理解.如果將矩陣和向量組密切地聯系起來，則線性方程組既可以看作矩陣方程，又可以看作向量組的線性相關性問題.看清了它們之間的聯系對于線性方程組的問題就不僅僅可以從矩陣的初等變換著手，還可以從向量的相關性作為切入點，這樣就為學生解決問題提供了方法，拓寬了思路.

3 注重學生思維能力的培養

教與學的過程中，我們除傳授數學知識外，更應注重培養學生發現問題的能力和數學思維能力，即所謂“授之與魚不如授之與漁”.在教學內容中滲透數學思想方法，對學生思維能力的培養是十分重要的.比如：在討論完矩陣的乘法之后，我們可以討論這樣一個問題：矩陣可不可以有類似于數的除法，如果可以怎樣來做？如果不可以為什么？這個問題提出以后，同學們眾說紛紜，因為數的除法實質就是被除數乘以除數的倒數，那么矩陣有所謂的“倒數”嗎？又因為矩陣的乘法不滿足交換律，矩陣這個所謂的“倒數”唯一嗎？有了這些想法，我們很自然的就引出了逆矩陣的概念，并且知道逆矩陣是唯一的.

另外，貫穿《線性代數》的突出思想方法之一就是“初等變換”的思想方法.利用初等變換理論作為基礎可建立矩陣的秩、逆，向量組與向量空間，線性方程組，矩陣的對角化，線性變換等理論，進而再考慮抽象空間到抽象空間上的線性變換.能夠掌握貫穿學科的若干思想方法其實就是找到了攀登整個學科高峰的捷徑，學會思想方法對學習線性代數是大有裨益的，而且對自學能力的培養會起到促進作用.

以上是在線性代數教學過程中的一些想法和實踐，希望能對教授此門學科的教師起到借鑒作用，也希望對學習線性代數的同學有所幫助.

〔1〕同濟大學數學教研室.線性代數:第2版[M].北京:高等教育出版社,1997.

〔2〕趙瓊.關于線性代數教學改革和教學實踐的思考.科教文匯，2007（8）（上旬刊）.

〔3〕吳天毅.線性代數教學內容改革的研究與實踐.天津輕工業學院學報數學專刊，2003（12）.

G642.4

A

1673-260X（2010）08-0207-02