基于邊集數組的最小獨立閉合環搜索算法實現

葉 寶,陳 義

(1.同濟大學土木工程學院,上海 200092;2.蘇州工業園區測繪有限責任公司,江蘇蘇州 215021)

基于邊集數組的最小獨立閉合環搜索算法實現

葉 寶1,2,陳 義1

(1.同濟大學土木工程學院,上海 200092;2.蘇州工業園區測繪有限責任公司,江蘇蘇州 215021)

控制網的閉合差檢驗是平差計算前的一個重要步驟,目的是發現原始觀測數據中的粗差并予以剔除,并評估外業觀測的質量。根據測量控制網的數據結構特點,提出基于邊集數組存儲結構的控制網最小獨立閉合環搜索算法的實現原理及具體過程。最后通過不同算例對算法的正確性進行驗證。

數據結構;邊集數組;最小獨立閉合環;算法

一、引 言

在測量平差計算前,為保證平差結果的正確性,防止觀測值可能含有粗差及系統誤差影響平差結果,無論是傳統的測量控制網,如導線網、水準網,還是 GPS控制網,都需對控制網中的各種多邊形閉合差進行檢核,以探測、剔除粗差,并評定觀測值的質量。因此,如何自動搜索出控制網的最小獨立閉合環成為一個核心問題。最小獨立閉合環搜索算法目前主要有三種：基于鄰接矩陣變換算法、基于生成樹和余樹變換算法、基于深度優先搜索算法[1]。一般都要用到數據結構知識,采用鄰接矩陣或鄰接表等存儲結構來實現。本文根據控制網的特點,采用了更為直觀的邊集數組的存儲結構,對生成樹和余樹變換算法進行了編程實現,并通過不同的例子,驗證了算法的正確性。

二、控制網的數據結構

1.數據結構的概念

數據結構是相互之間存在一種或多種特定關系的數據元素的集合。數據結構包含數據和數據關系兩方面的基本特征。

如圖 1所示,根據數據元素之間關系的不同特性,通常有四類基本數據結構：集合結構、線性結構、樹形結構、網狀結構。數據結構包括數據的邏輯結構 (logic structure)和物理結構 (physical structure)。其中數據的物理結構包括數據元素的表示和存儲以及數據元素之間關系的表示和存儲。通常數據結構采用數組法、鄰接表法、十字鏈表、鄰接多重表等基本的存儲結構表示。

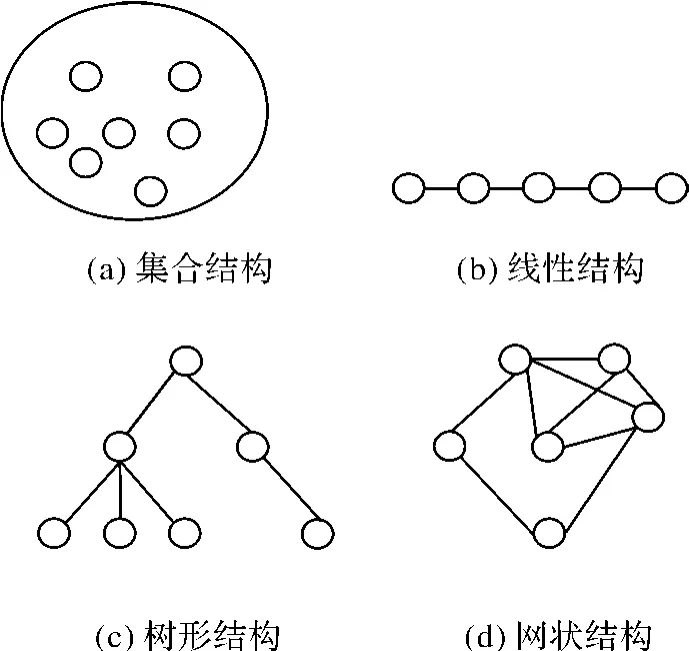
圖1 基本類型的數據結構

2.控制網的數據結構分析

根據圖 1和對測量控制網的特點分析,顯然控制點之間是任意的、多對多的復雜關系。因此控制網與數據結構中的網狀結構的概念一致。通過比較,可以建立控制網和圖之間如表 1所示的概念映射關系。

表 1 測量控制網與圖的概念間的映射關系

對于測量控制網而言,可以采用圖的鄰接矩陣等存儲結構表示。考慮到測量控制網的特點,總是由一系列控制點和邊組成的網狀結構,因此可以從圖的定義出發,采用點集數組和邊集數組的存儲結構(包括數據元素和數據元素關系的存儲)。二者均采用結構體數組,點集數組存儲控制點的所有信息,邊集數組存儲邊的所有信息,則所有控制點間的觀測值和相關關系都通過邊集數組來反映,如表 2所示。

表 2 測量控制網結構體數組存儲結構

三、算法原理分析

1.最小獨立閉合環搜索的概念

最小獨立閉合環是指控制網中含有觀測邊數最少且相互獨立的多邊形閉合環。是對控制網進行各種閉合差檢驗、定位粗差的基礎幾何模型。如前所述,測量控制網可映射為圖 (網)的數據結構。則問題的核心即歸結為對網的結構進行的最小獨立閉合環的分析確定。其內涵有二：①所搜索確定的閉合環最小,也即環的邊數最小,與網的“最短路徑”的概念一致;②各閉合環相互獨立,亦即每一個環中都至少有一條不屬于其他環的邊[2]。需要指出的是,對于一個網而言,其最小獨立閉合環的組合、構成情況并不唯一,只要找出其中的一組即可滿足定位粗差及評定觀測值質量的需要。

2.生成樹、余樹變換算法的原理

網的最小獨立閉合環搜索算法中以生成樹、余樹變換算法最為基礎,且搜索結果穩定[3]。該算法采用逆向思維,其原理是：首先對控制網進行簡化處理,將其“修剪”為一個稱為生成樹的樹形結構。所謂生成樹就是一個連通圖的最小連通子圖,其特點是含有圖中的全部 n個頂點,但只有足以構成一棵樹的 n-1條邊,如果在生成樹上添加一條邊,則必定構成一個環,因其使得它所依附的兩個頂點之間有了第二條路徑。因為測量控制網中不存在孤立的控制點,各點之間總是通過一定的觀測量、觀測邊發生著聯系,因此,對控制網而言,其總是一個連通網,對應的總是可以化簡為一棵生成樹。如圖2所示。

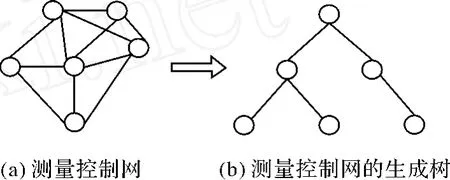
圖2 控制網數據結構轉化示意圖

因此,對于一個網,總可以通過一定的算法,將其分割為兩個部分,一是生成樹;二是生成樹的補集,稱為余樹,其中的每一條邊稱為余枝。將每一條余枝回代添加到生成樹上時,即構成一組閉合環,取其中路徑最短者為該余枝對應的閉合環,則全部余枝分別回代即構成一組獨立閉合環,因為根據“獨立”的定義,每個余枝對應的閉合環均至少有一條邊(余枝本身)不屬于其他環。為保證各閉合環是最小環,需要定義余枝添加到生成樹上的次序規則。

1)嘗試將全部余枝添加到生成樹上,取其中閉合環路徑長度最短者,優先添加到生成樹上,作為當前最小閉合環;

2)在生成樹的添加余枝后的當前子圖上,嘗試將其余的余枝添加到當前子圖上,取其中閉合環路徑長度最短者,優先添加到生成樹上,作為當前最小閉合環;

3)重復以上過程,直到所有 r個余枝均添加到生成樹上,即得到一組 r個最小獨立閉合環。

四、算法實現過程

基于生成樹和余樹變換算法的實現過程,控制網采用點集數組 P[n]和邊集數組 L[m]的結構存儲(均為結構體數組)。

1)采用BFS(寬度優先遍歷)算法,得到控制網的一棵寬度生成樹,生成樹也采用點集數組、邊集數組存放,則生成樹的點集與控制網的點集相同,邊集為控制網邊集的子集,將控制網的邊集設為全集,則生成樹邊集的補集即為生成樹的余樹的邊集數組。編程中只要將 BFS遍歷經過的邊的 V isited值標定為 true,即表示生成樹,否則為 false表示余樹,此即實現了對控制網邊集數組的分割處理。

2)將余樹中的余枝 (邊集數組 L[m]中 V isited值為 false的邊)逐一回代、添加到生成樹上(邊集數組L[m]中 V isited值為 true的邊),每添加一個余枝,得到一組閉合環,通過網的最短路徑算法求得該余枝兩端點間的最短路徑,比較所有余枝的最短路徑,選擇最短路徑最小的余枝,優先添加到生成樹上 (將其邊的Visited值標定為 true)。

3)重復2),直至所有的余枝都添加到生成樹上為止(邊集數組L[m]中所有邊的Visited值均為 true)。

由上述過程可見,關鍵是基于邊集數組的最短路徑算法的實現。本文采用經典的 Dijkstra算法,其實現過程是：定義兩個一維工作數組,一個是最短路徑長度數組 PathLength[n],此數組與點集數組P[n]相互對應,用以存放起始點 (余枝的一個端點)到生成樹中各頂點的路徑長度;另一個是最短路徑點名數組 PathName[n],用以存放起始點到其余各頂點的最短路徑的點序列。

1)初始化 PathLength[n]和 PathName[n]數組：起始點 S到其自身的邊長為 0,與其不相鄰接的點的邊長置為∞,與其相鄰接的點,通過一個成員函數 GetEdge(string PointA,string PointB),求出起始點到該點的邊的長度,并在點集數組 P[n]中將起始點 S的 Visited值標定為 true,表示起始點即默認為已知的最短路徑終點。

2)掃描 PathLength[n]數組：查找該數組中當前的最小值,凡是在點集數組 P[n]中 V isited值為true的點,其對應的在 PathLength[n]數組中的值均不予考慮,而在剩余的數組元素中查找最小值,并將其對應的在點集數組 P[n]中的點的 Visited值標定為 true,表示該點為自起始點出發的、當前最短路徑的終點,在 PathName[n]數組中記錄下該點 T,并記錄當前最短路徑值MinPath。

3)更新 PathLength[n]和 PathName[n]數組：以 2)中得到的當前最短路徑終點 T作為新的參考點,循環遍歷點集數組 P[n],查找計算 T點到達其他Visited值為 false的點的邊長 (P[n]中 Visited值為 true的點可視為已知最短路徑終點點集,不予考慮),如果遍歷的點與 T點相鄰接,并且MinPath與該點到 T點的邊長之和小于其在 PathLength[n]中的該點到起始點 S的路徑長度,則用MinPath與該點到 T點的邊長之和更新 PathLength[n]中該點到起始點 S的當前最短路徑長度值。

4)重復步驟 2)～步驟 3),直至點集數組P[n]中點的 V isited值全部為 true,即起始點到所有頂點的最短路徑均已查找得到,全部頂點均加入到已知最短路徑終點點集中為止。

最后需要說明的是關于成員函數 GetEdge (string Poin tA,string PointB),該成員函數的作用是分析網中各頂點是否相鄰及鄰接的邊長值,用以代替鄰接矩陣。用此函數省卻了復雜的構造鄰接矩陣的過程,并且避免了當網的頂點較多時,隨著鄰接矩陣的快速膨脹,需要大量占用內存空間的問題。其實現過程為,通過遍歷邊集數組L[m],分析確定出各頂點相鄰與否及鄰接的邊長值。對于無向圖,只要邊的起點和終點之間有一向相通即可視為相鄰,對有向圖,需要起點和終點之間雙向連通,才可視為相鄰。

五、應用及驗證

本文應用上述原理,采用 C#語言進行了編程實現。并采用幾個算例對算法的正確性進行驗證。

圖3為某市三等水準網,對該水準網進行閉合環搜索計算,共計算得到水準閉合環 23個,與原水準網中閉合環的實際情況完全一致;統計計算出的閉合環長度、閉合差均與水準網實際情況全部完全一致。采用其他幾個算例,同樣取得了準確的搜索計算結果。

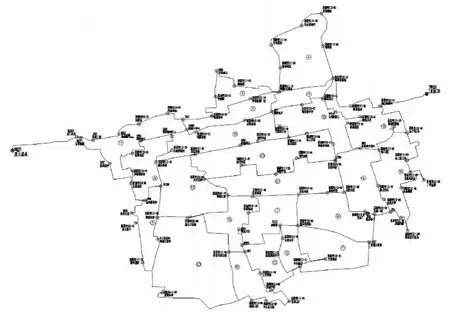
圖3 算例

六、結束語

本文根據測量控制網的特點,采用點集數組和邊集數組的存儲結構,實現了對網的最小獨立閉合環的自動搜索。避免了使用大矩陣,占用大量存儲空間的問題產生,并且使得數據的存儲結構更直觀、易于理解,便于數據的輸入存儲管理?？蓱糜趯嶋H生產及軟件設計中。

[1] 趙一晗,伍吉倉.控制網閉合環搜索算法的探討[J].鐵道勘察,2006,32(3)：12-14.

[2] 王金嶺,李陸勛.控制網最小閉合環信息自動生成算法[J].測繪通報,1995(1)：11-15.

[3] 鄒進貴,馮晨.控制網最小獨立閉合環搜索算法研究[J].地理空間信息,2008,6(6)：97-99.

[4] 馮琰,張正祿.最小獨立閉合環與附合導線的自動生成算法 [J].武漢測繪科技大學學報,1998,23(3)：255-259.

[5] 武漢測繪科技大學.測量平差基礎[M].3版.北京：測繪出版社,1996.

[6] WATSON K,NAGEL C,等.C#入門經典[M].3版.北京：清華大學出版社,2007.

[7] 嚴蔚敏.吳偉民,等.數據結構[M].C語言版.北京：清華大學出版社,2007.

Algorithm of Searching forM in imum Independent Closed-loop Based on Array of Edge Set

YE Bao,CHEN Yi

0494-0911(2010)12-0037-03

P207

B

2009-12-10

葉 寶(1977—),男,寧夏鹽池人,碩士生,研究方向為大地測量及測量數據處理。