精密定軌中變分方程的數值解法及其檢驗

洪 櫻,歐吉坤

(1.武漢紡織大學理學院,湖北武漢 430073;2.中國科學院測量與地球物理研究所,湖北武漢 430077)

精密定軌中變分方程的數值解法及其檢驗

洪 櫻1,歐吉坤2

(1.武漢紡織大學理學院,湖北武漢 430073;2.中國科學院測量與地球物理研究所,湖北武漢 430077)

變分方程的求解是衛星精密定軌中的關鍵步驟之一,通常都通過積分方法求解。首先從原理上詳細闡述一種新的數值方法求解變分方程,接著通過低軌衛星精密定軌仿真軟件對其精度和效率進行測試,且與常用數值積分方法的定軌結果進行比較。結果表明,在實際軌道確定中,采用新的數值方法可達到較高的精度要求,且算法的效率更高。

變分方程;數值方法;精密定軌;積分方法

一、引 言

在精密軌道確定中,如果知道初始狀態矢量以及力矢量,則可通過積分衛星的運動方程得到精密軌道。在求解初始狀態參數時,需用目前狀態相對于初始狀態矢量的偏導數,求解變分方程可得到構成狀態轉移矩陣的這種偏導數。所以,在積分運動方程的同時,必須求解變分方程[1-2]。對于變分方程的求解,許多學者都進行了研究和探討,提出了許多有效的方法,如簡化方法[3]、分析方法[3-4]、差分算法[5-6]、數值方法[2]等。其中數值方法是德國GFZ(GeoForschungs Zentrum)地學中心許國昌博士提出的一種新的一般化的求解變分方程的方法,其特點是通過差分代替微分使得變分方程轉化為線性代數方程組,進而根據其初值條件推出嚴格的遞推解。雖然文獻[2]中給出了數值方法嚴格的推導,但從未對該方法進行過數值檢驗和比較。使得該方法的應用和推廣缺少必要的數值依據。

本文在此理論基礎之上,部分地應理論原創者的要求,通過詳細的數值計算對這種新的求解變分方程的數值方法進行了分析。首先從原理上詳細闡述了這種新的數值方法的求解過程,然后通過精密定軌仿真軟件對其進行測試,且與常用的數值積分方法的結果進行了比較,從而證明了新解法的可行性和有益性。

二、新的數值解法

在軌道確定和預報過程中,需解算運動方程[1-2]

式中,˙X(t)為衛星的瞬時狀態向量;X(t0)為 t0時刻的初始狀態向量(記為 X0);F為時間 t、狀態向量 ˙X(t)以及動力學參數向量 y的函數,且

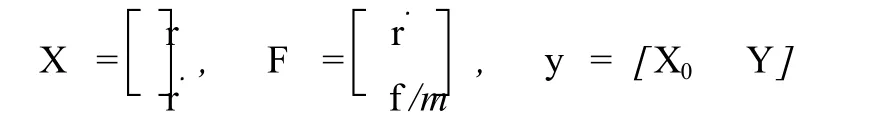
r和 ˙r分別為衛星的位置和速度向量;f為衛星所受力的向量和;m為衛星質量;Y是除位置、速度以外的動力學參數向量。

在運動方程(1)兩邊對 y求偏導數有

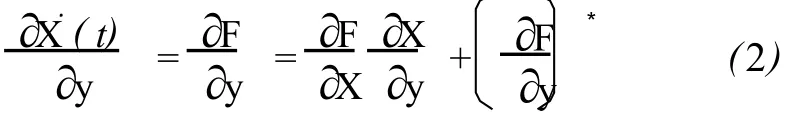
式中,＊號表示對 F中顯含的參數矢量 y的偏導,且記

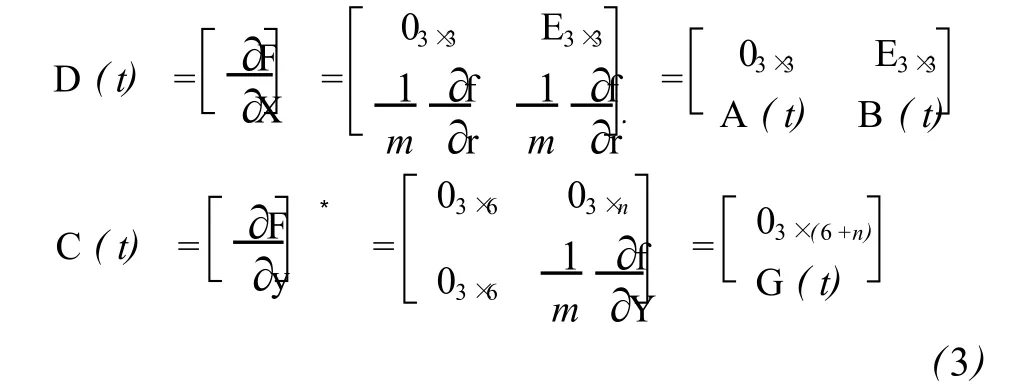
式中,E為單位陣,0為零矩陣,下標是其維數。則式(2)變為

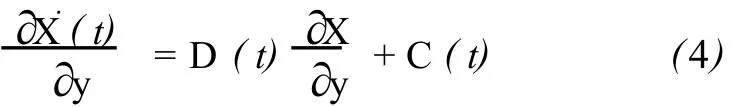
其解構成了狀態轉移矩陣,記為 Φ(t,t0)。則式(4)變為

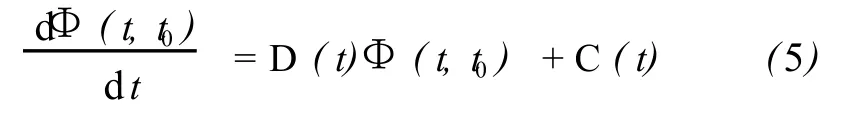
式(5)稱為變分方程。

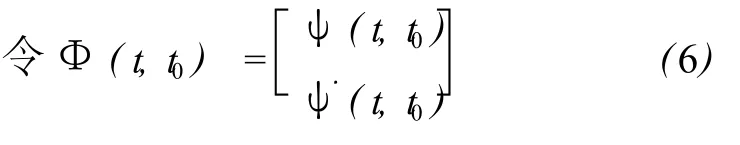
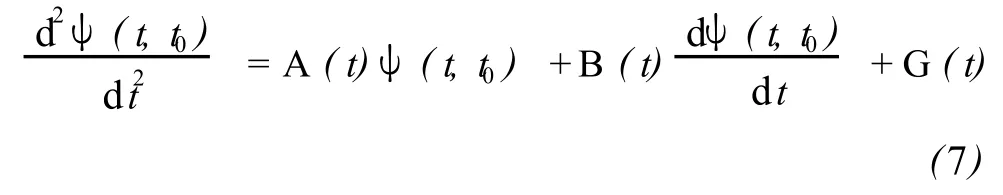
初值條件為

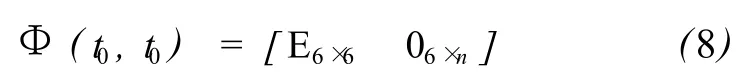
由于微分方程列與列之間是相互獨立的,因此只需考慮某列的方程的解。對于列 j,式(7)和初值條件式(8)可表示為

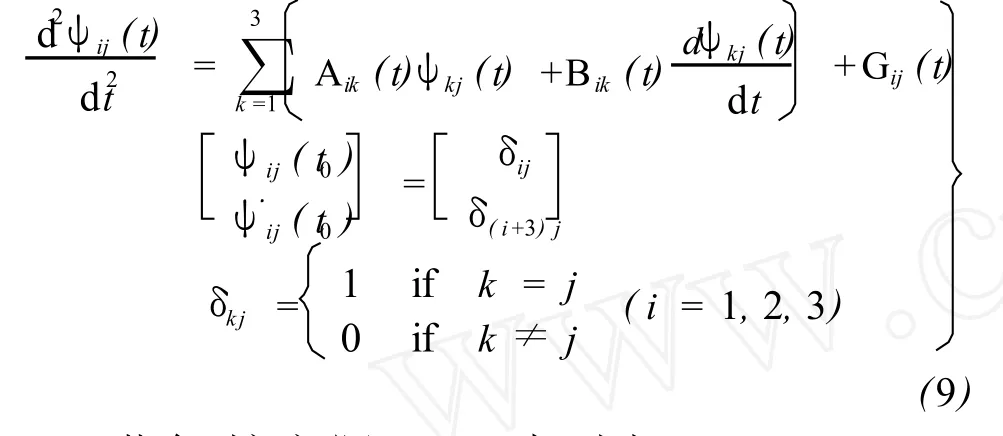
將式 (6)和式(3)代入式(5)得

若在時間間隔 [t0,t]中,步長 h=(t-t0)/m,則 tn=t0+nh,n=1,…,m,且

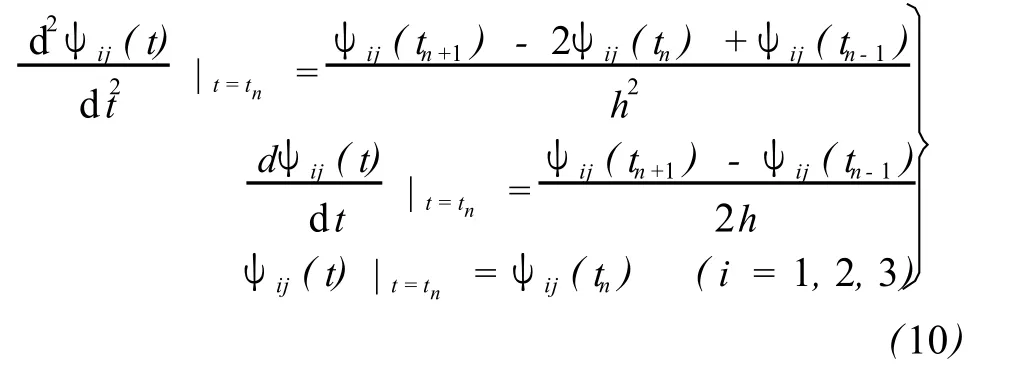
則式(9)變為

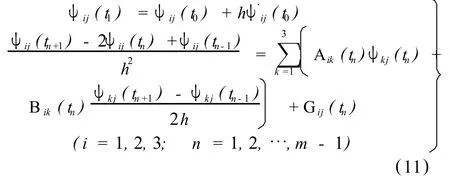
整理式(11)得

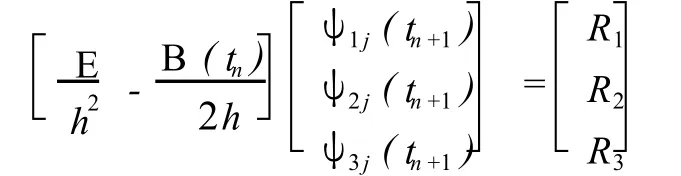
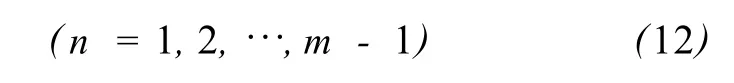
式中

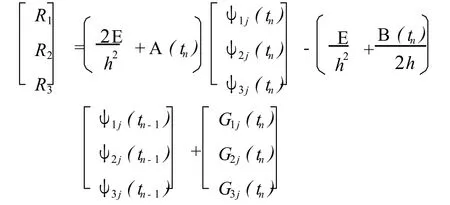
則可得到 ψ(tn+1),速度向量 ψ˙(tn+1)可利用式(10)計算得到。

三、數值檢驗算例

為了驗證數值方法的可靠性,以CHAMP衛星為例,在仿真過程中采用的動力學模型包括：70×70階的 JG M3重力場模型、DT M78大氣阻力模型、Wahr潮汐模型、N體攝動模型(行星位置由 JPL提供的行星歷表中精確地插值獲得)、光壓攝動模型(假設衛星帆板的法線方向始終與太陽垂直)以及廣義相對論攝動模型[7-9]。分別采用積分方法和數值方法計算狀態轉移矩陣,歷元間隔取為 10 s,其中積分方法采用穩定性較好、精度較高的 RKF7(8)法起步、10階的第 II種類型的 collocation-PECE算法[8]。由于低軌衛星的偏心率較小,所以可采用固定步長進行計算[1]。取初始時刻為 2002年 1月 3日 0時 0分0秒,軌道初始狀態(慣性系下位置和速度)為x0=701 111.972 7 m, y0=-368 100.205 1 m, z0=6 723 471.518 4m, vx0=-4 695.158 9 m/s, vy0=6 017.559 8m/s, vz0=838.240 2m/s。為了避免比較數據過于龐大,這里僅列出狀態轉移矩陣的部分矩陣元,并且最少保留到數值方法與積分方法有差異的位數。將積分方法的計算結果記為Φ1,數值方法的計算結果記為Φ2,計算結果列于表 1。

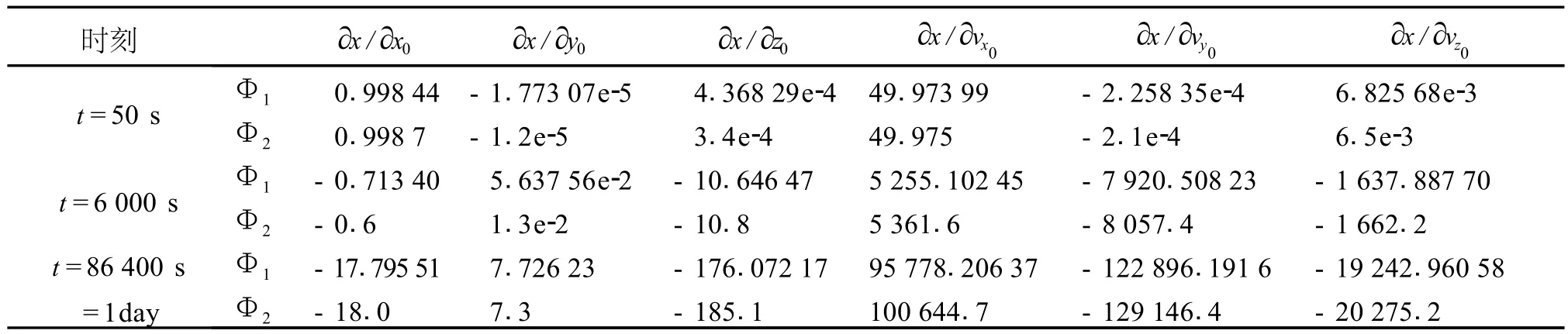
表 1 積分方法和數值方法的計算結果比較

首先需要指出的是,隨著積分弧段的增加,積分方法所花的時間迅速增長。在此算例計算中,積分方法和數值方法均積分了 1條軌道 (6個狀態方程),并且都需計算加速度的偏導,而積分方法比數值方法多積分 6×6=36個變分方程。因此,積分方法共積分了 42個方程,而數值方法只積分了 6個方程。當再增加一個動力學參數時,積分方法需積分6+7×7=55個方程,而數值方法仍僅需積分 6個方程,所以,待估動力學參數越多,數值方法節省時間的優越性就越明顯。當然其前提條件是要保證計算的精度。

表 1列出了積分方法和數值方法計算的狀態轉移矩陣中的部分矩陣元。從表中可以看出,當弧段較短時,兩種方法計算出的狀態轉移矩陣中矩陣元的值相差不大,對于數值較大的矩陣元仍有 3～4位數字相同。但隨著積分弧段的增加,兩種方法的計算結果差異變大。

由于狀態轉移矩陣描述的是初始狀態和模型參數的變化對動力學系統演化的影響,即變分方程的解——狀態轉移矩陣是無量綱的,無法直接描述其精度。而在求解初始狀態參數時,需要用到狀態轉移矩陣,因此狀態轉移矩陣的精度會影響到最終的定軌結果。所以,不妨以精密軌道確定的結果來考察變分方程解法的效果。同樣采用上述仿真軟件并模擬 100min(略大于低軌衛星的運行周期)的P3碼偽距觀測值用于軌道確定,歷元間隔為 10 s。分別采用數值法和積分法求解變分方程,利用批處理算法得到的軌道初始狀態的改正量列于表 2中。

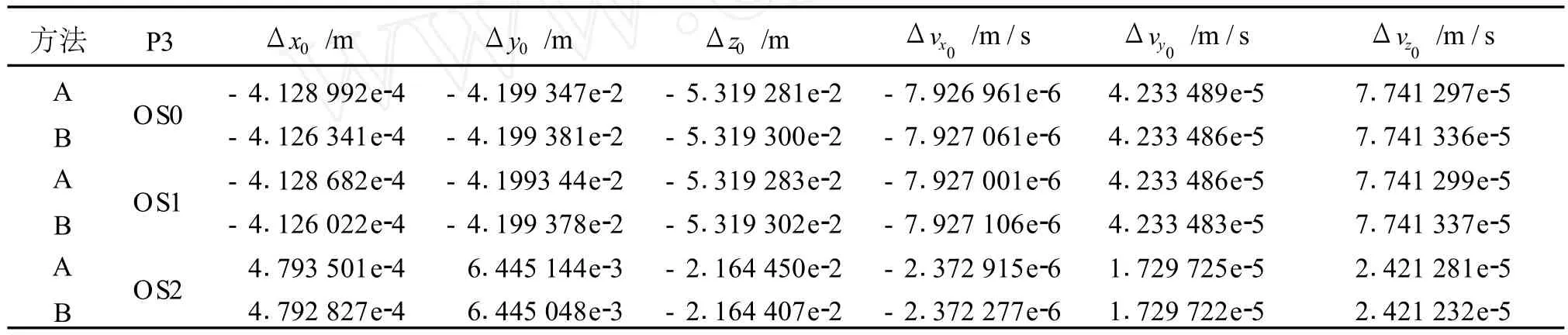
表 2 兩種方法求解變分方程得到的軌道初始狀態的改正量

表 2中方法A表示采用數值法求解變分方程,方法B表示采用積分法求解變分方程;OS0表示無誤差的 P3碼觀測值,OS1表示只包含接收機鐘差的P3碼觀測值,OS2表示包含接收機鐘差、GPS衛星精密鐘差和觀測偶然誤差的 P3碼觀測值。

從表 2可以看出,在相同觀測條件下,用數值法和積分法求解變分方程得到的軌道初始狀態的改正量相差甚小,坐標分量達到微米的數量級,而速度分量達到 10-8～10-10m/s的數量級。

四、結束語

本文首次驗證了變分方程的數值解算方法,從而確認了定軌中一種全新的算法流程,即不再需要通過繁復的積分方法來求解變分方程。該方法并不像其他方法那樣受外部條件的限制,如軌道弧長、動力學模型的復雜程度等;且算法的推導嚴格,程序易于實現。從低軌衛星軌道確定結果來看,在相同 GPS觀測條件下采用數值法求解變分方程的精度與積分法求解變分方程的精度相當。由于積分方法的精度較高,可以推論這種新的數值方法的精度也是較高的。此外,從算法的效率來看,積分方法比數值方法多積分 n2(n為待估參數個數)個變分方程。因此,這種新的數值方法在實際軌道計算中更有效。

[1] 李濟生.人造衛星精密軌道確定[M].北京：解放軍出版社,1995：189-219.

[2] XU GC.GPS Theory,Algorithms andApplications[M]. Berlin：Springer-Verlag,2003：217-277.

[3] 劉林,張強,廖新浩.人衛精密定軌中的算法問題[J].中國科學：A輯,1998,28(9)：848-856.

[4] 張強,劉林.軌道改進中計算狀態轉移矩陣的分析方法[J].天文學報,1999,40(2)：113-121.

[5] 張家祥,汪琦,楊捷興,等.彗木相撞預報[J].中國科學：A輯,1996,26(3)：280-288.

[6] 胡小工,黃輝,廖新浩.狀態轉移矩陣的差分算法及其應用[J].天文學報,2000,41(2)：113-122.

[7] 徐天河,楊元喜.基于能量守恒方法恢復 CHAMP重力場模型[J].測繪學報,2005,25(2)：75-81.

[8] MONTENBRUCK O,G ILL E.Satellite Orbits-Models, Methods andApplications[M].New York：Springer-Verlag,2000：53-154.

[9] BOCK H.EfficientMethods for Deter mining Precise Orbits of Low Earth Orbiters Using the Global Positioning System[D].Switzerland：Institute für Geod?sie und Photogrammetrie Eidg,2003：77-85.

Numerical Solution of Var iational Equation for Precise OrbitDeterm ination and Its Test

HONG Ying,OU Jikun

0494-0911(2010)12-0001-03

P228

B

2010-07-20

洪 櫻(1980—),女,湖北荊門人,碩士,講師,主要從事衛星精密軌道確定與預報理論研究。