視頻編碼線性碼率控制模型
(西安電子科技大學 ISN國家重點實驗室,西安 710071)
1 引 言
視頻壓縮的最終目的是占用較少的資源,獲得較高的視頻質量。實際應用中,考慮可用資源受限的條件下,為使接收端獲得質量最好的恢復視頻質量,碼率控制成為視頻編碼器的重要組成部分[1]。碼率控制是指為編碼器確定編碼參數對視頻進行編碼,使得接收端恢復視頻的質量在信道帶寬、編碼器緩沖區大小等受限的條件下盡可能高。目前,H.264/AVC[2]的參考軟件[3]將JVT-G012[4]和JVT-W042[5]作為其推薦使用的碼率控制方案。
現有的碼率控制機制普遍通過建立碼率-量化步長(R-Qstep)模型[6-9]為編碼器確定編碼參數,比如JVT-G012和JVT-W042采用的二次模型[7]。在H.264/AVC中,量化步長不能直接作為編碼參數。通過R-Qstep模型確定量化步長后,需要將量化步長轉換為量化參數才能對視頻進行編碼。由于Qstep到QP的轉換過程存在舍入誤差,采用R-Qstep模型進行碼率控制會使最終確定的QP所對應的量化步長與計算所得的量化步長之間存在差異,進而使得編碼碼率與目標碼率之間存在大的偏差、編碼器緩沖區狀態產生大的波動,并使恢復的視頻質量下降。本文通過理論推導與實驗驗證得到碼率(R)與QP的直接對應關系,提出了R-QP模型,并利用該模型進行速率控制。仿真結果驗證了所提模型的準確性。
2 數學模型
視頻失真與編碼碼率之間的關系為[10]
(1)
式中,D為編碼視頻的均方誤差(Mean Square Error,MSE)失真,δ和r為模型參數,RT表示紋理信息編碼比特數。恢復視頻的峰值信噪比(PSNR)與D之間的關系為
P=10×lg(2552/D)
(2)
式中,P為恢復視頻的PSNR。分別對式(1)、式(2)左右兩邊同時取對數并聯立可得:
2×lg255-0.1·P=(1-2r)·lgRT+2·lgδ
(3)
進而有式(4)成立:
P=algRT+b
(4)
式中,a和b為模型參數。式(4)表明P與lgRT之間存在線性關系。文獻[11]中指出,P與QP之間存在著線性關系,則得:
lgRT=α·QP+β
(5)
式中,α和β為模型參數,QP表示量化參數(QP)。式(5)表明lgRT與QP之間存在線性關系。
為驗證式(5)所示的模型,表1統計了不同序列的lgRT與QP之間的相關系數。由表1可以看出,相關系數的絕對值幾乎接近1,表明lgRT與QP之間存在線性關系,證明了本文提出模型的正確性。

表1 lgRT與QP之間的相關系數統計結果Table 1 The statistical results of the correlation coefficient between lgRT and QP
3 QP的計算
本文依據相鄰幀之間的相關性確定當前幀的QP。用Rttbe(i,j)表示第i個GOP中的第j幀的目標紋理信息編碼比特數(The Number of Target Texture Bits Encoded,Rttbe),Ratbe(i,j)表示第i個GOP中的第j幀的實際紋理信息編碼比特數(The Number of Actual Texture Bits Encoded,Ratbe),QP(i,j)表示第i個GOP中的第j幀的量化參數。每個GOP中前兩幀的QP按照已有的方法確定。對第i個GOP中的第j(j>2)幀確定QP的具體方法如下:
(1)判斷當前幀的前兩幀的QP是否相同。若QP(i,j-1)不等于QP(i,j-2),則直接利用前兩個已編碼幀的數據,計算R-QP模型的參數α和β,如式(6)、(7)所示,繼而可計算出當前幀的QP。
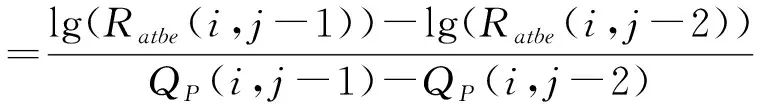
(6)
β={QP(i,j-1)×lg(Ratbe(i,j-2))-
QP(i,j-2)×lg(Ratbe(i,j-1))}·
{QP(i,j-1)-QP(i,j-2)}-1
(7)
(2)若QP(i,j-1)等于QP(i,j-2),首先采用式(8)檢測已編碼幀的QP是否準確,若式(8)成立,即已編碼幀的目標比特數的均值和實際編碼比特數的均值之間的差值小于門限值T1,則說明已編碼幀的QP選擇較為合理,進而可以采用滑動窗口中的數據計算當前幀的QP。

(8)
式中,K為滑動窗口的長度,實驗中取值為5。
其次,依據式(9),在滑動窗口記錄的各幀實際編碼比特數中尋找與當前幀目標比特數最相近的幀:
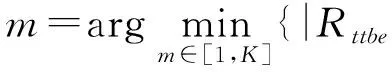
(9)
若當前幀的目標比特數和第j-m幀的實際編碼比特數的差值小于門限值T2,如式(10)所示,根據相鄰幀之間的相關性,可以采用第j-m幀的QP對當前幀進行編碼:
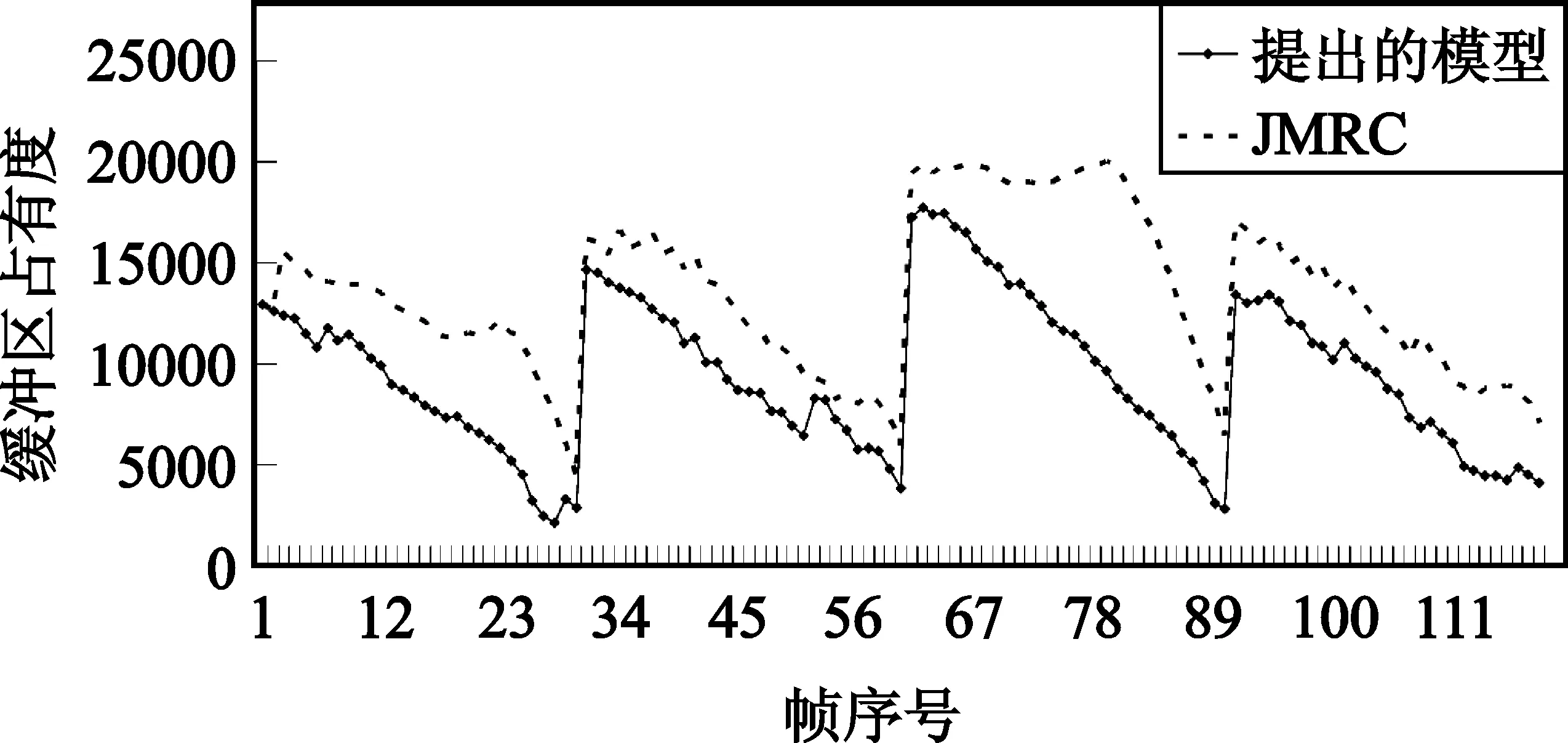
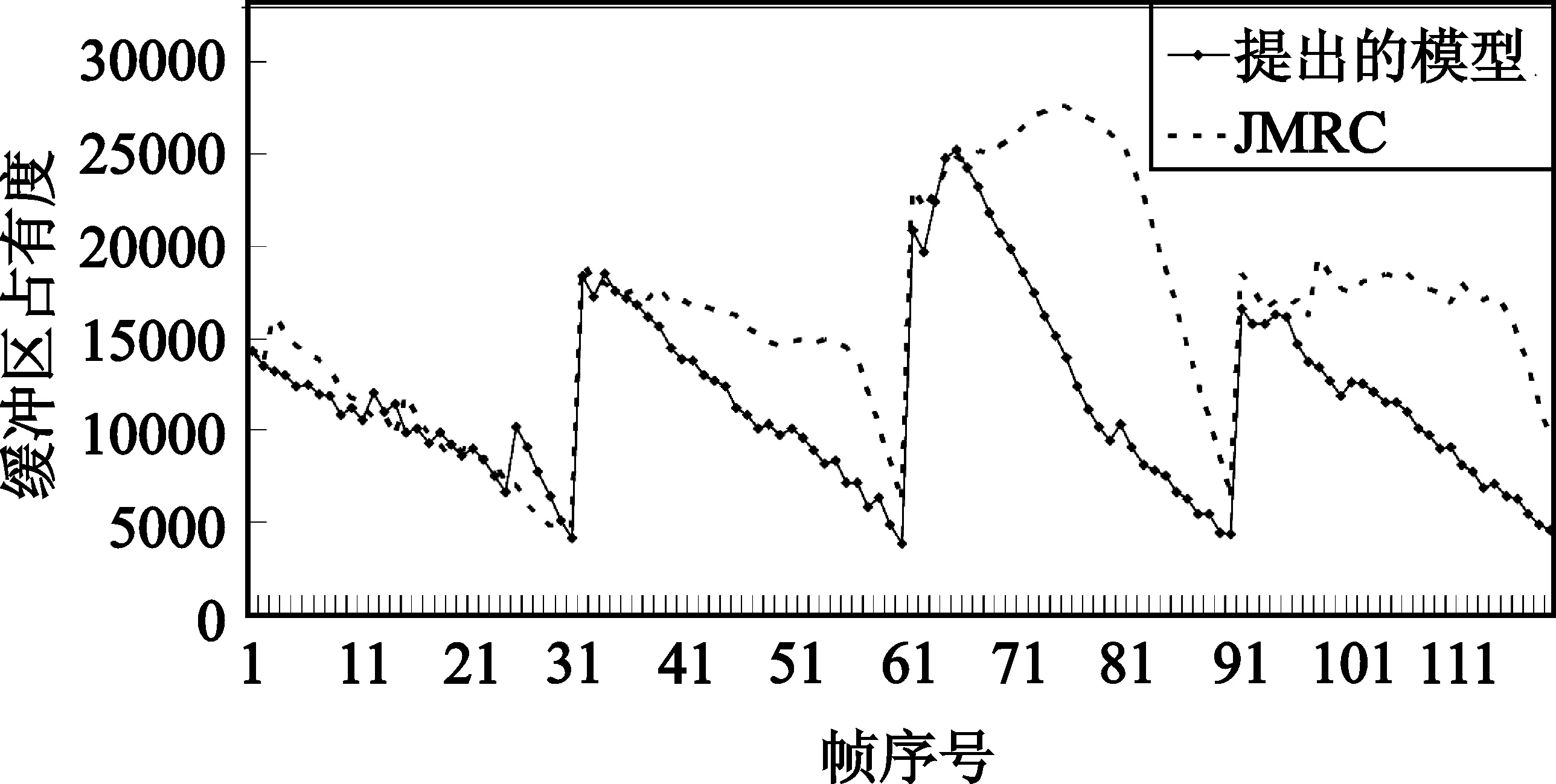
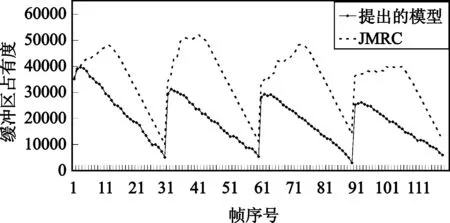
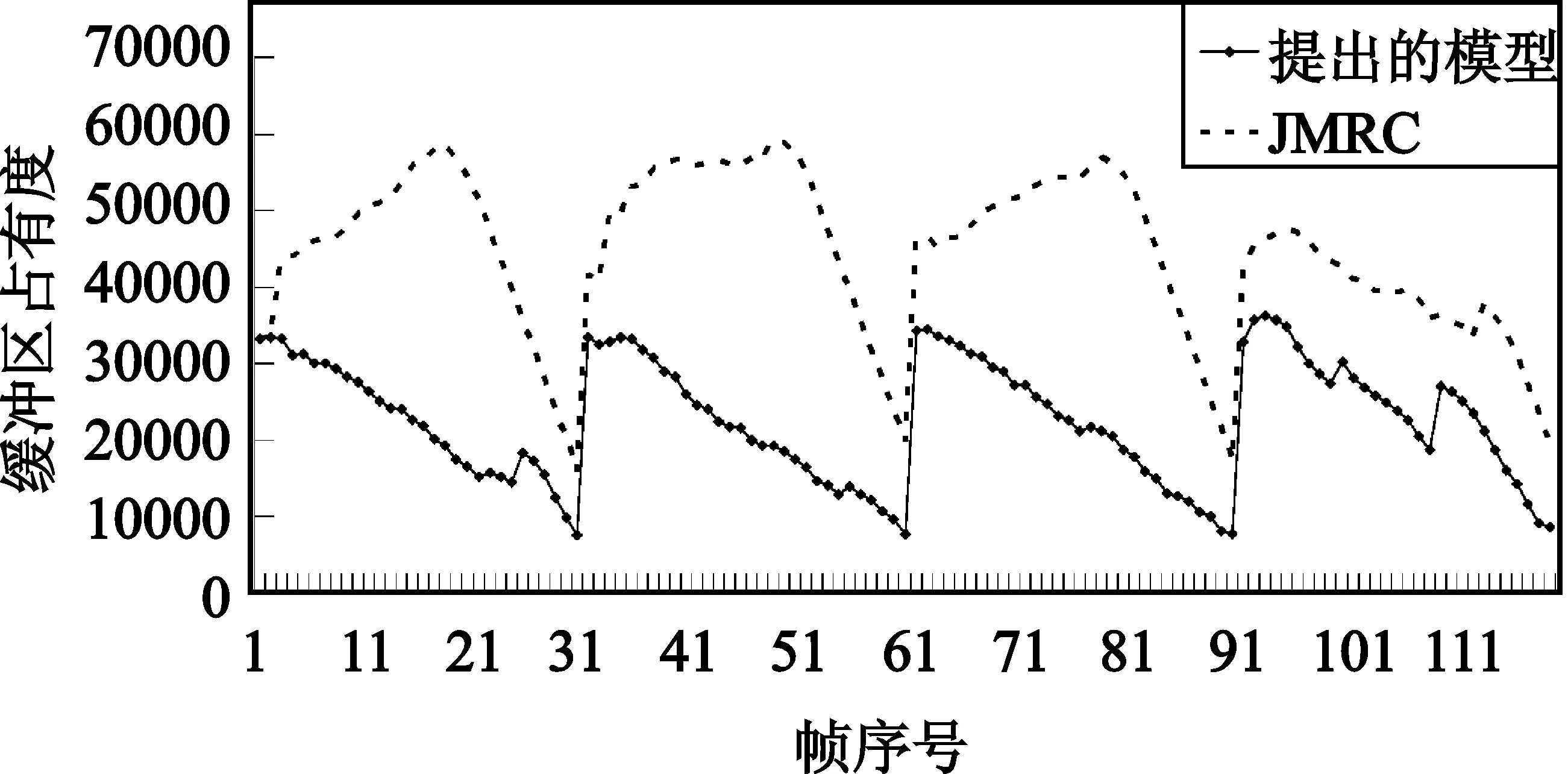
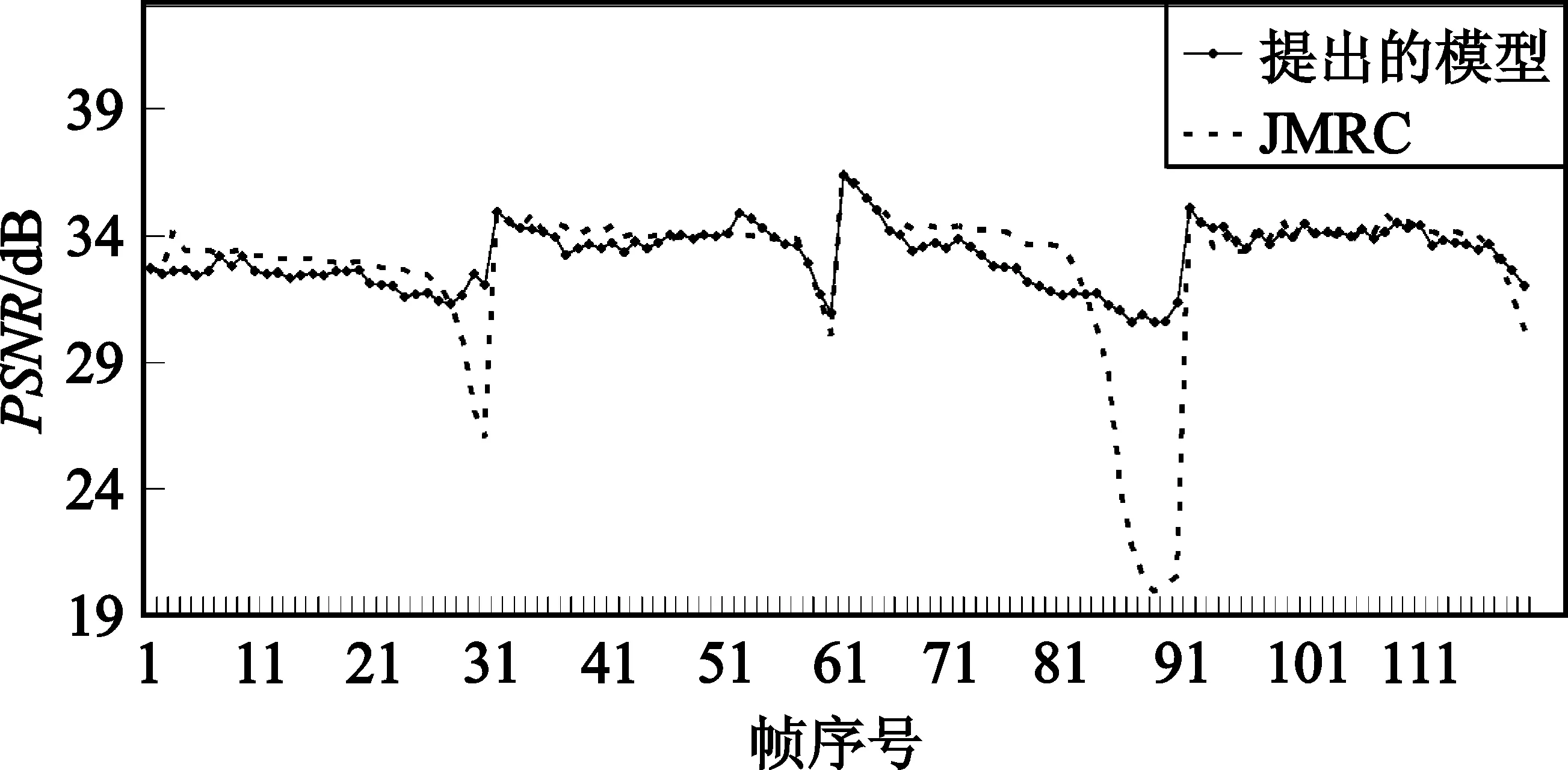
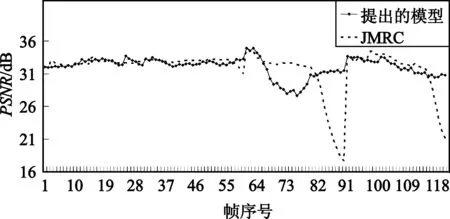
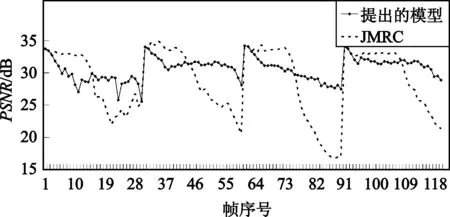
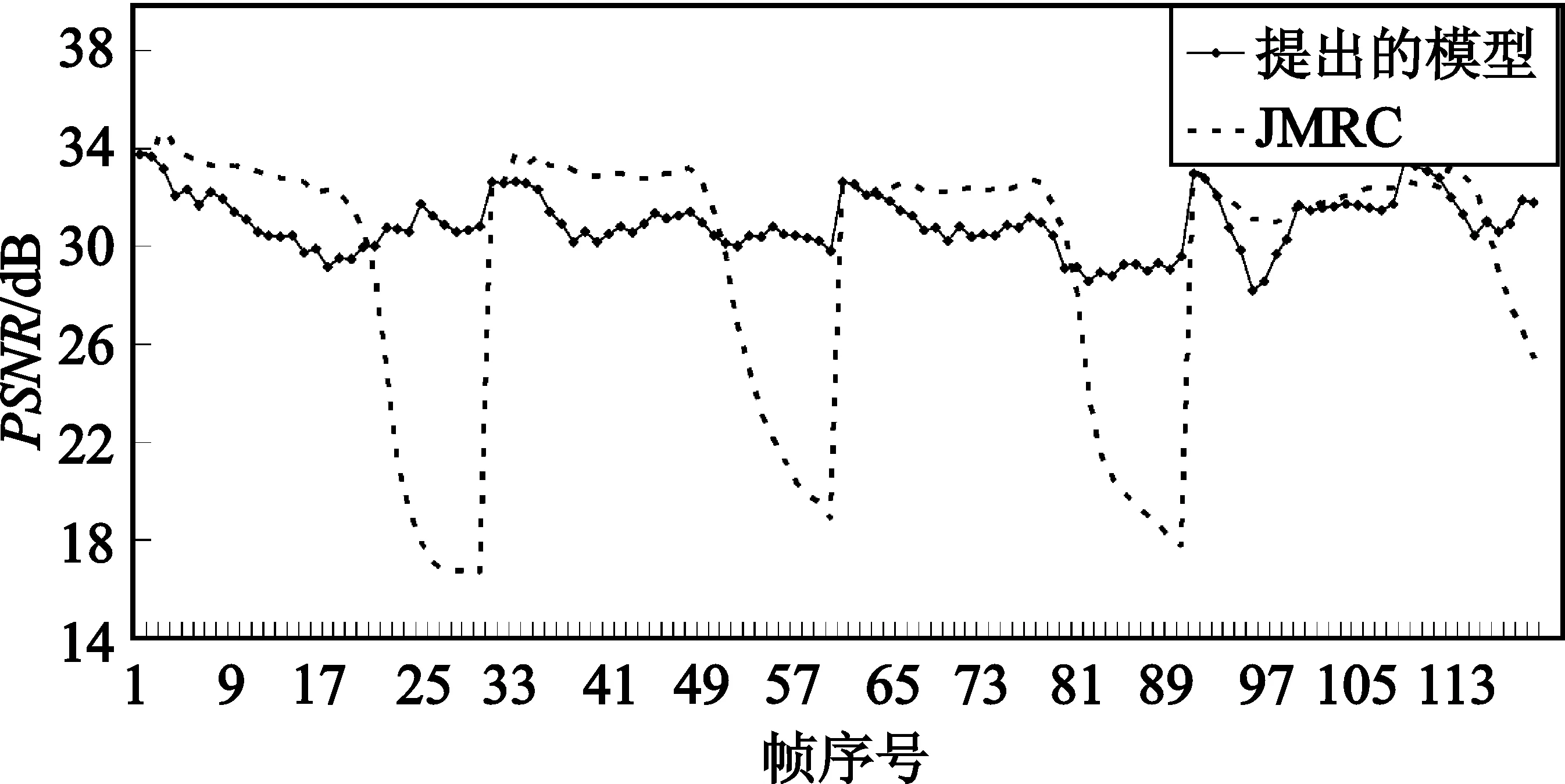
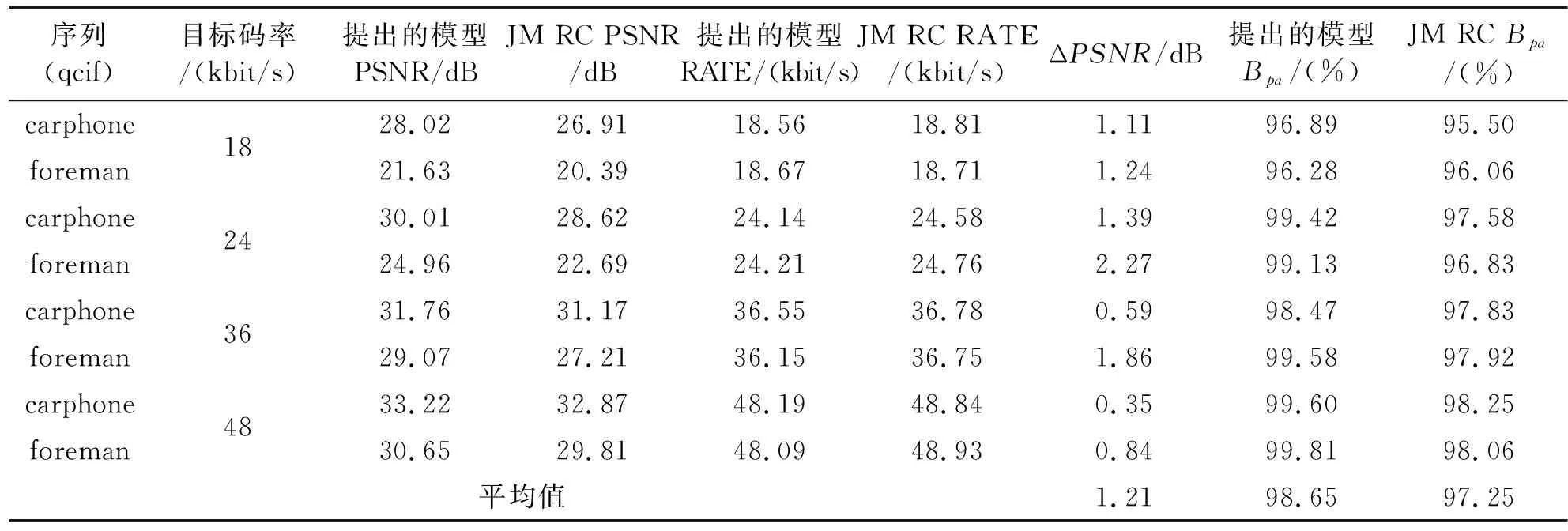
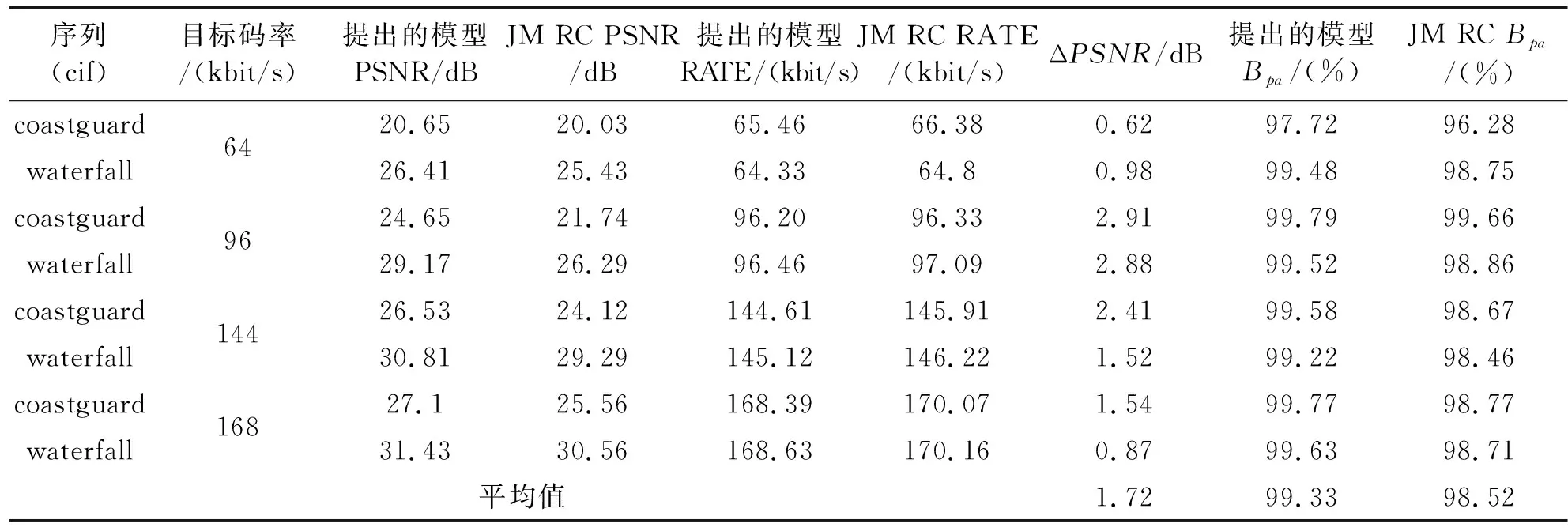
|Rttbe(i,j)-Ratbe(i,j-m)| (10) 若式(8)或者式(10)不成立,則通過判斷前一幀的實際紋理信息編碼比特數Ratbe(i,j-1)與當前幀的目標紋理信息編碼比特數Rttbe(i,j)的大小,確定當前幀的QP,如式(11)所示: (11) 分別采用本文提出的模型與JVT-W042(記為“JM RC”)進行測試。在不同目標碼率條件下,通過比較編碼碼流的緩沖區狀態、實際編碼碼率以及恢復視頻的PSNR驗證提出模型的有效性。實驗中采用H.264/AVC 參考軟件JM15.1[3]為實驗平臺進行碼率控制。采用IPPP編碼結構,GOP長度選為30,qcif序列的目標碼率分別為18 kbit/s、24 kbit/s、36 kbit/s和48 kbit/s,cif序列的目標碼率分別為64 kbit/s、96 kbit/s、144 kbit/s和168 kbit/s。在碼率控制中,緩沖區大小Bs設置為目標碼率,當緩沖區占有度Bc大于Bs的0.8倍時,進行跳幀處理。 圖1比較了提出的模型與JVT-W042的緩沖區占有度。由圖1可以看出,提出的模型其緩沖區占有度比 JVT-W042的緩沖區占有度小。 (a)carphone(48 kbit/s) (b)foreman(64 kbit/s) (c)carphone(72 kbit/s) (d)foreman(120 kbit/s)圖1 緩沖區占有度之間的比較曲線Fig.1 Comparison curves of the current buffer fullness 圖2給出了采用提出的模型與JVT-W042進行碼率控制后的恢復視頻質量PSNR的比較。由圖2可以看出,與JVT-W042相比,提出的模型其PSNR變化較為平緩,質量更加穩定。由于JVT-W042碼率控制不夠準確,使得緩沖區占有度較大,出現跳幀,從而,導致了視頻質量的急劇下降。 (a)carphone.qcif(48 kbit/s) (b)foreman.qicf(64 kbit/s) (c)carphone.cif(72 kbit/s) (d)foreman.cif(120 kbit/s)圖2 PSNR比較曲線Fig.2 Comparison curves of PSNR 表2和表3分別給出了qcif和cif序列在采用提出的模型和JVT-W042進行碼率控制之后的實際編碼碼率和恢復視頻的PSNR,其中,ΔPSNR表示提出模型的平均編碼質量的增益;Bpa表示實際編碼碼率與目標碼率之間的相近程度,可由式(12)計算得到: Bpa=(1-|T-A|/T)×100% (12) 式中,T表示目標碼率,A表示實際編碼碼率。 由表2和表3可知,與JVT-W042相比,采用提出的模型進行碼率控制,得到的恢復視頻的質量有所提高:對于qcif格式的序列,PSNR平均提高了1.21 dB;對于cif格式的序列,PSNR平均提高了1.72 dB;對于這兩種序列,PSNR平均提高了1.46 dB。此外,提出模型的編碼碼率要比JVT-W042的碼率更接近目標碼率。 表2 提出的模型和JM RC 的PSNR以及RATE統計結果Table 2 The statistical results of PSNR and RATE gained by the proposed model and JM RC 表3 提出的模型和JM RC 的PSNR以及RATE統計結果Table 3 The statistical results of PSNR and RATE gained by the proposed model and JM RC 為提高視頻編碼器碼率控制的性能,本文提出了一種碼率-量化參數模型。該模型能夠直接確定量化參數,避免了已有算法中通過量化步長確定量化參數的過程中的舍入誤差。實驗結果表明,提出的模型可以使緩沖區占有度更小,實際編碼碼率更接近目標碼率,視頻質量波動更小。此外,與H.264/AVC采用的碼率控制機制相比,提出的模型可以獲得更高的PSNR。由于該模型具有良好的性能,可廣泛應用于各種速率控制算法以及其它使用率失真模型的場合,以提高視頻編碼器的率失真性能。 參考文獻: [1] Chen Z C, Ngan K N. Recent advances in rate control for video coding [J]. Signal Processing,2007,22(1):19-38. [2] ITU-T Recommendation H.264 and ISO/IEC 14496-10 AVC Standard,Advanced Video Coding for Generic Audiovisual Services[S]. [3] Heinrich-Hertz-Institute. JVT Reference Software Version JM15.1 [CP/OL].(2009-7-07) [2010-06-20]. http://iphome.hhi.de/suehring/tml/download/old-jm/jm15.1.zip. [4] Li Z G, Pan F, Lim K P,et al. Adaptive Basic Unit Layer Rate Control for JVT [DB/OL].[2010-06-20]. http://wftp3.itu.int/av-arch/jvt-site/2003-03-Pattaya/JVT-G012r1.zip. [5] Leontaris A, Tourapis A L. Rate Control Reorganization in the Joint Model (JM) Reference Software [DB/OL]. [2010-06-20]. http://wftp3.itu.int/av-arch/jvt-site/2007-04-SanJose/JVT-W042.zip. [6] Chiang T,Zhang Y Q. A New Rate Control Scheme Using Quadratic Rate Distortion Model [J].IEEE Transactions on Circuits and Systems for Video Technology,1997,1(7):264-250. [7] Lee H, Chiang T, Zhang Y. Scalable rate control for MPEG-4 Video [J].IEEE Transactions on Circuirts Systems on Video Technology,2000,10(6):878-894. [8] Wang N,He Y. A New Bit Rate Control Strategy for H.264 [J]. ICICS-PCM,2003, 15(18): 1370-1374. [9] 萬帥,常義林,楊付正,等.一種新的視頻編碼二次率失真模型及其性能分析[J].電子與信息學報,2007,29(5):1136-1139. WAN Shuai, CHANG Yi-lin,YANG Fu-zheng,et al. A New Quadratic Rate Distortion Model for Video Coding and Its Performance Analysis [J]. Journal of Electronics & Information Technology,2007,29(5):1136-1139.(in Chinese) [10] Choi J. Distortion Policy of Buffer-constrained Rate Control for Real-time VBR Coders [J]. IEEE Transactions on Image Processing, 1999, 8(4): 537-547. [11] Wang H, Sam K. Rate-Distortion Optimization of Rate Control for H.264 With Adaptive Initial Quantization Parameter Determination [J]. IEEE Transactions on Circuits and Systems for Video Technology,2008,18(1):140-144.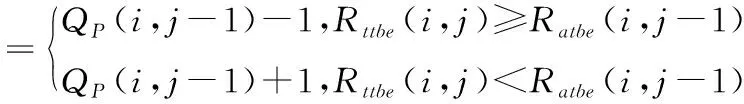
4 實驗結果
5 結 論

