構造分支數為4的對合線性變換

李 平， 孫 兵， 李瑞林， 李 超

（國防科技大學 數學與系統科學系，湖南 長沙 410073）

0 引言

分組密碼的設計主要關注兩方面的性能，第一是算法本身的安全性，第二是算法的軟硬件實現效率。大多數分組密碼均采用SP輪函數的結構，文獻[1]研究了分組密碼S盒輸出分量函數的密碼學性質，文獻[2]研究了一類P置換的設計方法。P置換要實現盡可能高的擴散性以抵抗差分線性等密碼攻擊手段，需要線性變換的分支數盡可能高。對合性質能夠使得加解密完全一致，達到節省資源提高效率的目的。目前 AES，Camellia，FOX，SMS4等算法都使用了達到最優分支數的線性變換，分支數均為5，但都不是對合的。為了能夠像Feistel型分組密碼一樣做到加解密一致，在擴散層中采用對合型線性變換就非常必要，目前韓國密碼標準ARIA算法就采用了一個對合的線性變換作為其擴散層，并且分支數達到了最優。

基于以上優點，設計盡可能好的分支數以及對合的線性變換是近來的熱點問題。由于異或運算和循環移位易于實現，結合這兩種技巧來設計線性變換的方法逐漸得到廣泛的應用。中國設計的無線局域網中使用的SMS4算法就是采用這種方法設計的擴散層[3]。現在已有的研究基礎上，給出了三類達到次最優分支數的對合型線性變換的構造。

1 基礎知識

下面給出給出線性變換分支數以及對合的定義：

B(L)=mX≠in0(W （X ) + W(L ( X)))。

根據分支數的定義，可知， B (L)≤ m+1。特別地，當B ( L ) = m+1時，稱該線性變換為最優線性變換；當 B ( L) = m時，稱該線性變換為次最優線性變換。

現有的構造最優線性變換的方法包括如下一些方法：

①循環矩陣構造[4]，AES算法擴散層基于該方法設計。文獻[4]指出，與一般的隨機矩陣相比，循環矩陣所對應的線性變換達到最優的概率更大。文獻[2]進一步指出，如果還要求變換為對合變換，則這樣的對合型線性變換的分支數最大只能達到4；

②組合方法構造[5]，FOX算法擴散層基于該方法設計；

③Hadamard矩陣構造，NESSIE計劃中提交的分組密碼算法Khazad[6]與Anubis[7]的擴散層基于該方法設計；

④Cauchy矩陣構造[8]。

除這幾種常見的構造方法之外，利用循環移位和異或運算也可以構造分支數達到最優的線性變換。假設，用Xi表示將X循環左移i位，其中0 ≤ i≤ n m-1，則利用循環移位和異或運算可以表示從的一類線性變換。文獻[9]給出了利用循環移位和異或運算設計最優線性變換時的一些條件這種方法特別適合于軟硬件的實現，效率高。但是，已有的基于該構造方法給出的最優線性變換均不是對合變換。

2 三種構造次最優對合線性變換的方法

上一節中基于循環移位結合異或運算的方法均是將X視為整體進行循環移位和異或運算，對X的分量進行考慮，當 4m= 時，給出分支數達到4時的對合線性變換的三種構造方法。

證明：根據分支數的定義，必要性顯然。

下面證明充分性，根據分支數的定義，只需按輸入X的重量來分別討論：

首先根據條件輸入向量滿足 W (X)= 1，則輸出向量滿足W(Y)≥ 3 ；

當輸入向量滿足 W (X) = 2 時，假設此時輸出 Y =L(X)的重量 W (Y)= 1 。由于L是對合的，可考慮其逆變換L-1=L，由已知條件可知 X =L-1(Y)的重量 W (X)≥ 3。與W(X) = 2 矛盾，故輸出 Y =L( X)的重量 W (Y)≥ 2 ；

當輸入向量滿足 W (X) = 3 時，由于輸出是非零的，那么必有 W (Y)≥ 1。

綜合以上3種情況，可知 B (L)≥ 4。

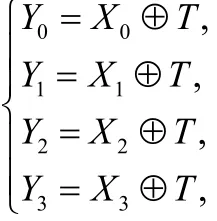
則線性變換L滿足對合性質且分支數為 B ( L ) = 4。

證明：首先證明L的對合性，由L的定義：Y0⊕Y1⊕Y2⊕ Y3=X0⊕X1⊕X2⊕ X3， 故 T = ( X0⊕ X1⊕X2⊕ X3)i = (Y0⊕Y1⊕Y2⊕Y3)i ,又易知：

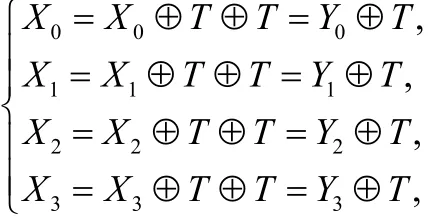
從而L為對合變換。

下面證明L的分支數為4，不妨設輸入 X = ( X0,0,0,0)，X0≠ 0 ，則容易計算：

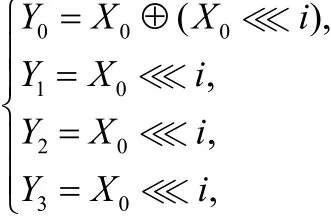
可知， Y1≠0, Y2≠0, Y3≠ 0 ，故 W (Y)≥ 3；又由于L是對合的，由定理 1可知 B (L)≥ 4。另一方面，可設輸入X=(X0,0,0,0)中的 X0為全1向量，將其代入L的定義驗證可知，輸出 Y =L( X)的重量 W (Y)= 3 ，由分支數定義，取所有可能的輸入輸出重量之和的最小值，故分支數為4。

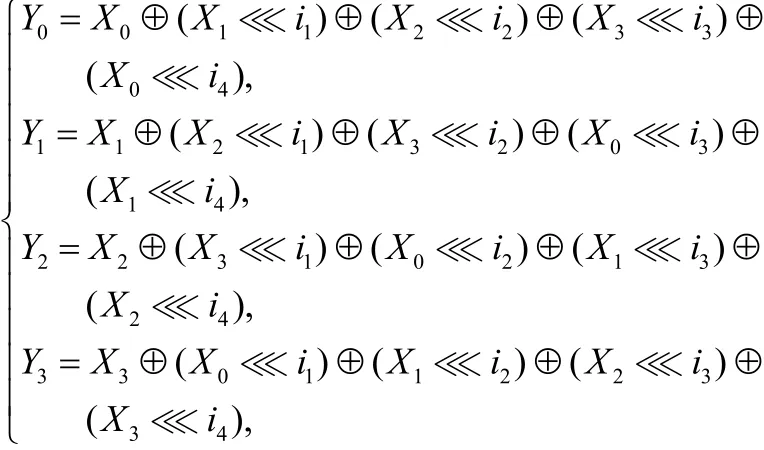
則線性變換L滿足對合性質且分支數為 B ( L) = 4。

證明：首先證明L的對合性，由L的定義，可做如下循環移位：并計算 Y0⊕(Y1i1) ⊕(Y2i2) ⊕ (Y3i3) ⊕ (Y0i4)可得:

X0= Y0⊕ ( Y1i1) ⊕ ( Y2i2) ⊕ ( Y33) ⊕ (Y0i4)，同理可得：

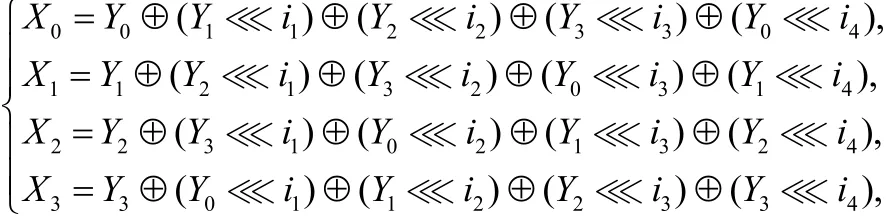
從而L為對合變換。類似構造1的證明可知L的分支數為4。

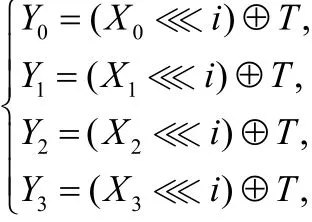
則線性變換L的分支數為 B ( L) = 4，進一步，當n為偶數且i = n /2時，L是對合變換。

證明：首先證明L分支數為4，根據分支數的定義，只需按輸入X的重量來分別討論：

（1）當輸入X的重量 W (X)= 1時，輸出 Y =L ( X)的重量 W (Y)≥ 3；

不妨設輸入 X = ( X0,0,0,0)， X0≠ 0 ，則容易計算：

可知， Y1≠ 0 , Y2≠0, Y3≠ 0 ，故 W (Y)≥ 3 。

（2）當輸入X的重量 W (X) = 2 時，輸出 Y =L ( X)的重量 W (Y)≥ 2 ；

不妨設輸入 X = ( X0, X1,0,0), X0≠0, X1≠0,則容易計算:

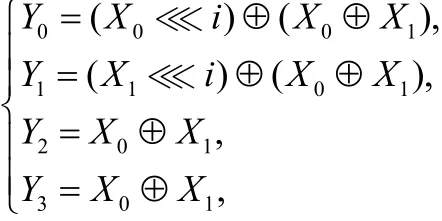
若 X0⊕X1=0，則Y0≠0, Y1≠0，此時W(Y)= 2 ；若X0⊕X1≠0，則Y2≠0, Y3≠0，此時W(Y)≥ 2 。從而當W(X) = 2 時， W (Y)≥ 2 。

當輸入X的重量 W (X)= 3 時，輸出非零，所以必有W(Y)≥ 1；綜上并且注意到（2）中存在輸出 W (Y)=2的情況，由于分支數的定義，故 B ( L ) = 4。

下面證明當n為偶數且 i = n /2時，L是對合的：由Y0⊕Y1⊕Y2⊕ Y3= ( X0⊕X1⊕ X2⊕X3)i ,故 T = X0⊕ X1⊕X2⊕ X3=( Y0⊕Y1⊕Y2⊕Y3)■ i ，則：

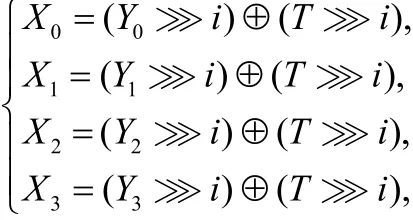
令T'= Y0⊕Y1⊕Y2⊕Y3，則 Ti =T '2 i，從而：

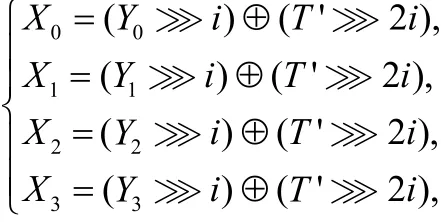
當n為偶數且 /2i n= 時，有2i n= ，此時：

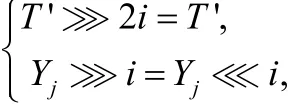
故：

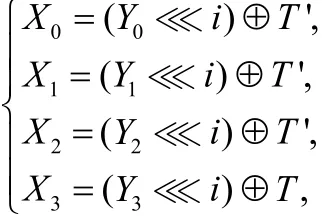
這表明L為對合變換。

3 結語

介紹了分支數較好的對合型線性變換在密碼算法中的重要作用，以及主要的構造方法。研究了如何利用循環移位和異或運算構造從的線性變換，使得分支數達到次最優，并且是對合的。給出了三種具體的構造方法，并分別給出了證明。進一步需要研究，在利用這幾類線性變換作為擴散層組件時，密碼算法是否能夠有效地抵抗各種密碼分析方法，尤其是截斷差分密碼分析。同時，利用提出的設計方法能否找到分支數達到最優的線性變換也是下一步繼續研究的課題。

[1] 李強,李超.Camellia算法中S盒輸出分量函數的等價表示[J].通信技術,2008,41(11)：126-128．

[2] 王念平,金晨輝,余昭平.對合型列混合變換的研究[J].電子學報,2005,33(10)：1917-1920．

[3] 國家商用密碼管理辦公室．無線局域網產品使用的 SMS4密碼算法[EB/OL].(2005-02-05).[2010-01-10].http：//www.oscca.gov.cn/UpFile/200621016423197990.pdf.

[4] DAEMEN J, KNUDSEN L R, RIJMEN V. The Block Cipher Square[C]//FSE 1997, LNCS 1267. Springer-Verlag, Berlin, 1997： 149-165.

[5] PASCAL J, SERGE V. Pergect Diffusion Primitives for Block Ciphers Building Efficient MDS Matrices[C]// SAC 2004, LNCS 3357. Berlin：Springer-Verlag,2005： 84-99.

[6] BARRETO P, RIJMEN V. The Khazad Legacy-level Block Cipher[EB/OL]. (2000-11-13) [2010-01-10]. http：//www.crypt onessie.org.

[7] BARRETO P, RIJMEN V.The Anubis Block Cipher[EB/OL].(2000-11-13).[2010-01-10]. http：//www.cryptonessie.org.

[8] WILLIAMS F M, SLOANE N. The Theory of Error-Correcting Codes[M].Holland：North-Holland Pub. Co.,1977.

[9] 王金波.基于循環移位構造最優線性變換[C]//密碼學進展——中國密碼學會 2007年會論文集.成都：西南交通大學出版社,2007：306-307.