三維TIN與TIN相交算法及其在巖土工程中應用

張 芳， 朱合華

（1. 北京市勘察設計研究院有限公司，北京 100038；2. 同濟大學巖土及地下工程教育部重點實驗室、地下建筑與工程系，上海 200092）

三維TIN與TIN相交算法及其在巖土工程中應用

張 芳1， 朱合華2

（1. 北京市勘察設計研究院有限公司，北京 100038；2. 同濟大學巖土及地下工程教育部重點實驗室、地下建筑與工程系，上海 200092）

地質剖面圖或籬柵圖是地質勘探人員了解描述地質結構的常規手段之一。該文實現了從三維地質模型中提取任意剖面圖的基礎算法，即三維TIN與TIN相交算法。該算法作為許多商業圖形軟件的核心算法，屬于商業秘密。該文詳細論述了該算法原理、數據結構設計、計算流程等。該算法作為實現自主知識產權的三維巖土工程系統的一部分，既能靈活的設定曲面形狀與方向，又能夠顧及到復雜的約束條件。最后針對具體的工程實例檢驗了算法的正確性和應用價值。

計算機應用；TIN與TIN相交算法；剖面；空間分析

地質剖面圖或籬柵圖是地質勘探人員了解地質結構常規的手段之一。為了從三維地質模型中獲得剖面信息，通常采用任意剖面去切割地層模型，三維TIN與TIN相交算法是實現該項功能的基礎算法之一，另外，該算法也是地層建模及人工交互、GIS空間分析等功能的支撐算法，是許多三維地質、油田和 GIS商業軟件的核心算法。

此外，在幾何造型、計算機模擬、GIS、計算機輔助設計等領域中，往往要處理大量的復雜圖形布爾運算問題，尤其是三維問題涉及到大量的三維TIN與TIN的相交處理，現在世界流行的CAD圖形平臺 ACIS、PARASOLID、Open CAS.CADE、DESIGNBASE等都很好的解決了這個問題，但由于涉及核心算法，源代碼沒有公布。三維TIN與TIN相交算法與二維相交算法相比復雜程度有量級上的區別，作為核心，屬于商業秘密，本文探索該算法在三維上的實現，作為實現自主知識產權的某三維巖土工程系統的一部分。

1 TIN與TIN相交算法

空間三角形與三角形的相交問題是研究三維TIN與TIN相交算法的基礎（但不是全部），Martin Held[1]和 Tomas M?ller[2]提出的算法在其中最具代表性，Olivier Devillers[3]對這兩種算法進行了比較。本文根據已知地層鉆孔離散數據的特點，考慮搜索半徑與搜索效率，編制實現了三維TIN與TIN相交算法。

1.1 算法原理

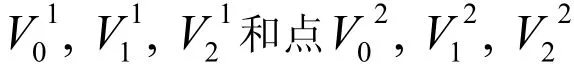
（1） 根據文獻Tomas M?ller[2]首先寫出平面π2(或π1)點法式方程（見圖1）

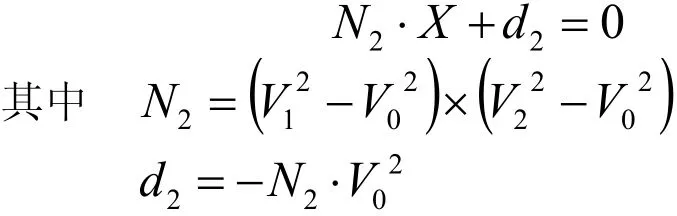
（2） 分別利用三角形 T1(或 T2)的三點到平面π2(或π1)的有向距離()的正負還是零來判斷三角間的平行、共面還是可能相交三種情況。

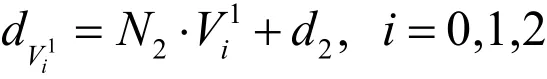
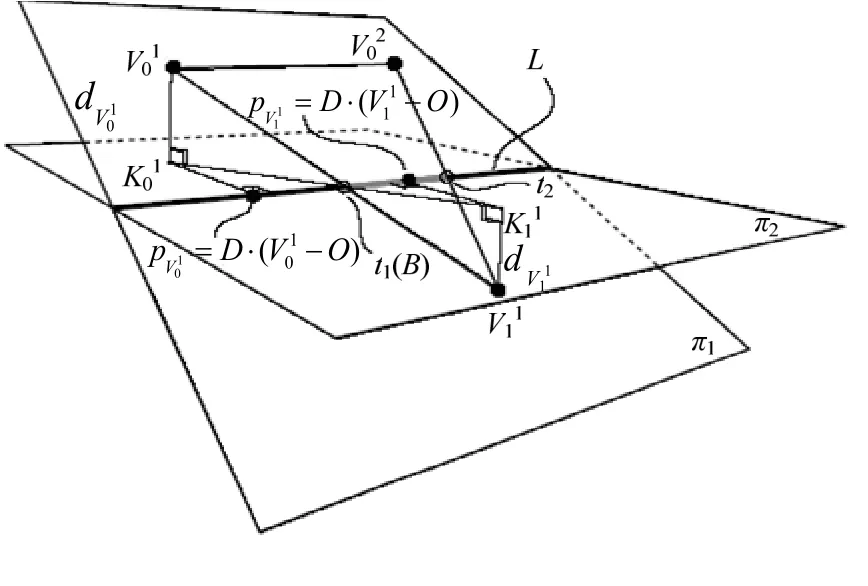
圖1 三角形求交線（Tomas M?ller，1997）

（3） 對于可能相交的三角形，會出現兩種情況，如圖2(a)是真實的相交，圖2(b)是相離的。本文對這兩種情況統一處理，首先生成三角形 T1（或T2）與平面π2（或π1）的交線P1P2，再生成三角形T2（或T1）與平面π1（或π2）的交線Q1Q2（如圖2），顯然二者都位于交線L上，是交線L的一部分。

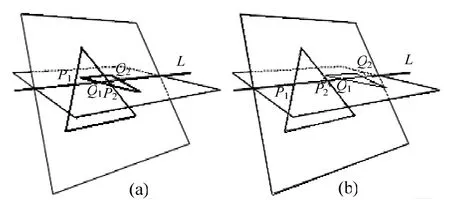
圖2 三角形求交線（Tomas M?ller，1997修改）

（4） 判斷21PP 和21QQ 的關系，如果兩者有重疊部分，則提取重疊線段即為所求，否則說明兩三角形是相離的。

（5） 對于交線21PP （或21QQ ）的生成采用空間線段與無限平面求交來實現。

1.2 數據結構設計

本文數據結構的設計采用面向對象思想，以類的形式體現。考慮到書寫方便這里不再詳細介紹點、線段、三角形、四面體四種幾何基元以及TIN類、相交算法等類的數據結構，僅給出類體系框圖一張，如圖3所示，本算法的類作為基類存在于該類系中。圖中的類服務于“資源場”（“資源場”：顧及到人類對地理空間的認知，把整個地理空間（上至大氣層、構筑物、地表、下到地下空間的地質體、構筑物等等）定義為一個資源場，且為唯一資源[4]）。“資源場”下有工程對象和地質對象兩種幾何對象。

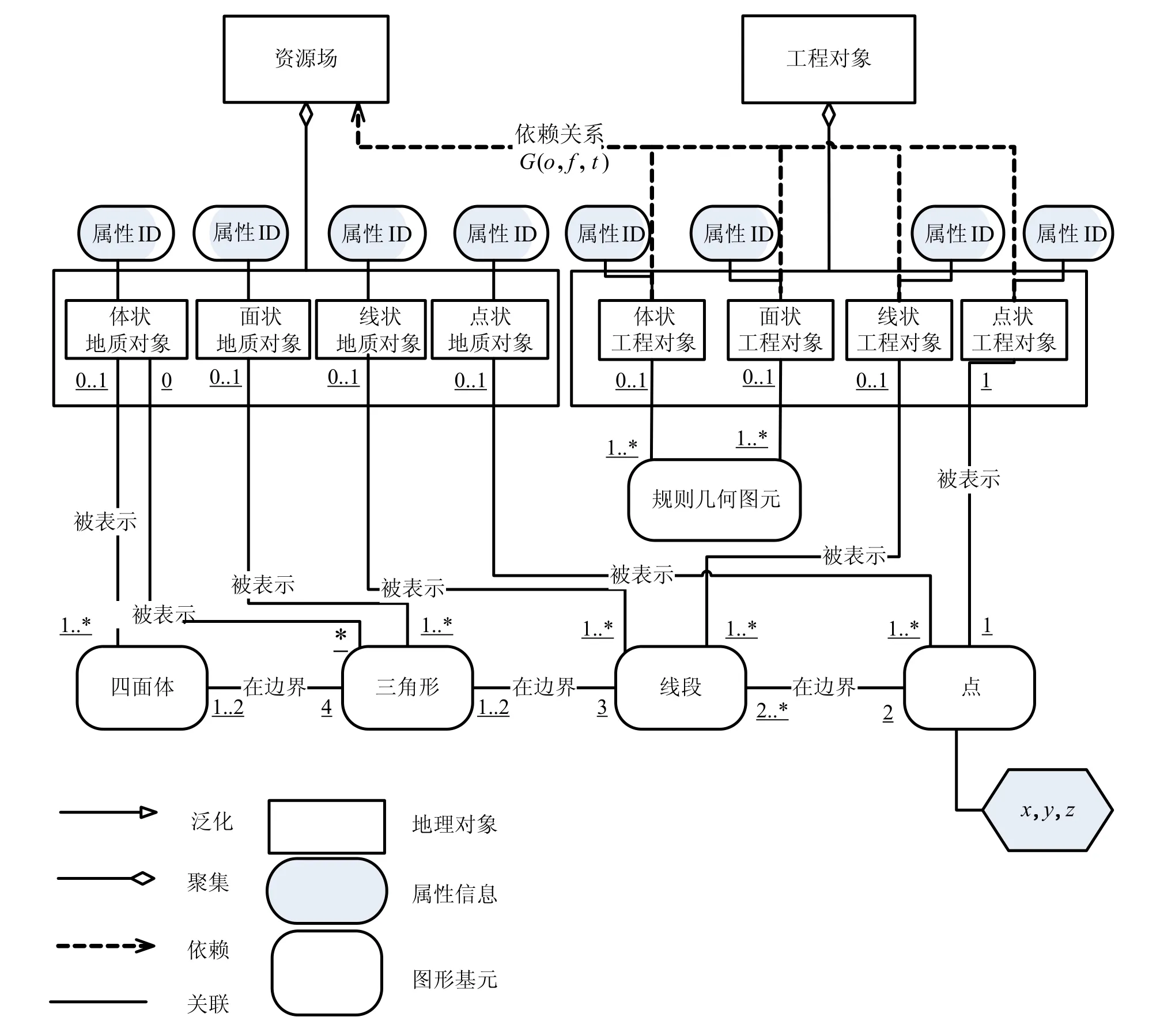
圖3 混合數據模型

1.3 算法特點

本算法是基于空間三角形與三角形之間的相交實現的，且以約束 Delaunay算法重構三角網，特別地在做約束Delaunay剖分時，算法中引入從局部平面 Delaunay剖分到整體三維Delaunay剖分的思想，很好地解決了三維空間約束條件下的Delaunay剖分生成問題，這個本質決定了以此算法為基礎的分析功能的特色，即能靈活的設定曲面形狀與方向，且能夠顧及到復雜的約束條件。算法流程圖如圖4所示。

2 算法應用實例

作為算法的驗證實例，主要從驗證算法的穩定性、可靠性和實用性角度選用實例，旨在驗證該算法做為開發系統底層算法的基本功能，這與工程的復雜性是兩個概念，復雜的實例可基于這些基本功能擴展而來，當然任何一個底層基本算法不可能獨立運行而不依賴其它達到整體效果。

基于實測鉆孔資料，應用上述算法，可實現地層區域的任意剖切，本算法支持空間曲面剖分，能夠用任意方向，任意形狀的三維空間剖面對進行地層剖切顯示，充分體現了算法區別其它算法的優勢。

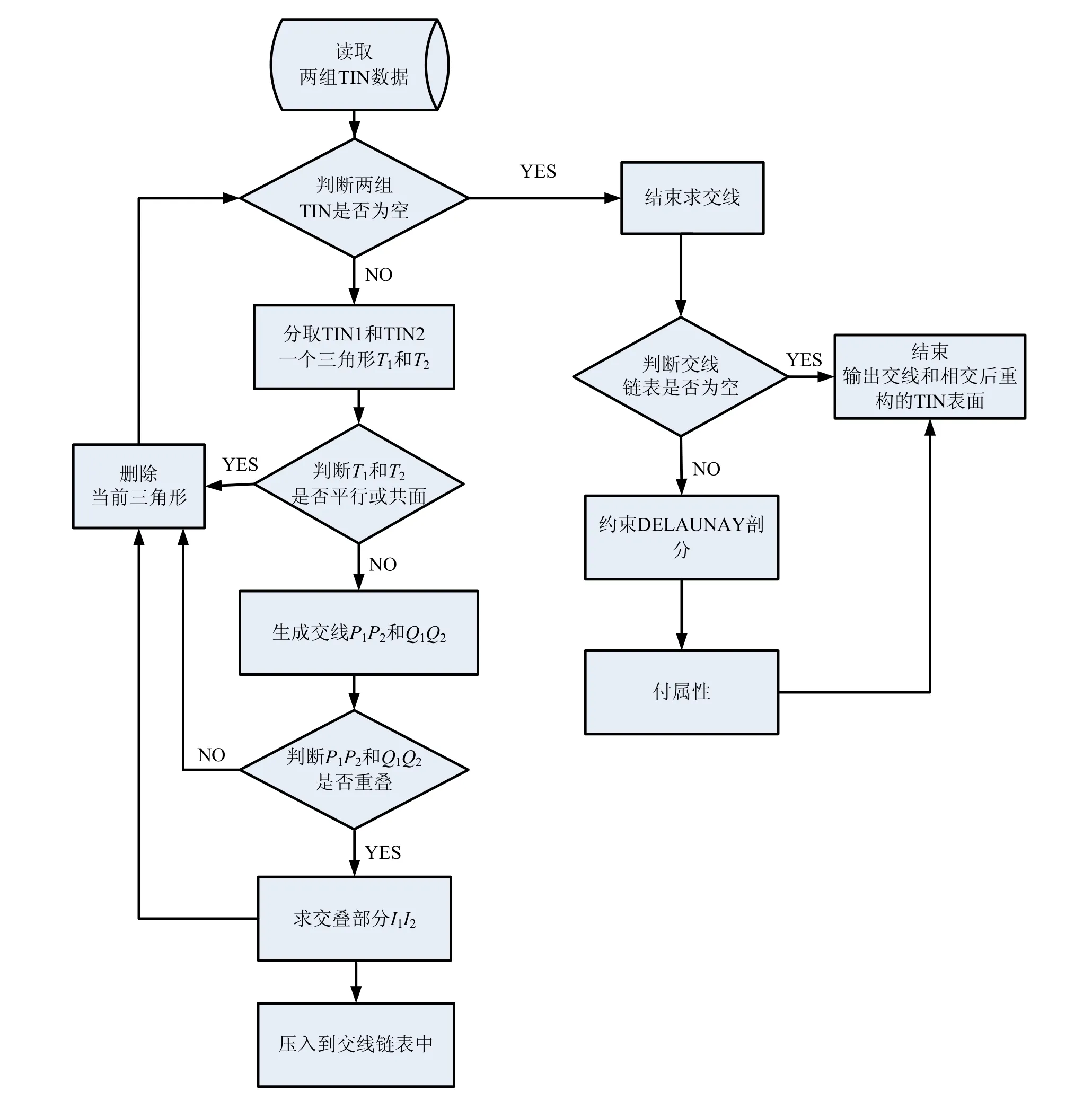
圖4 三維TIN與TIN相交算法流程圖

2.1 地層的任意剖切

本文從數據庫中提取某處地層的鉆孔數據共25個，含244個離散數據點，生成11層不同厚度和分布的土層，土層編號以上海標準土層為準，用不同顏色加以區別，如圖5所示，地層中有一處尖滅和一處透鏡體，分別為第1⑤-1層（紅色表示）和第1⑥層土（黑色）。對該地層做任意剖切，其中剖切面（空間曲面）與地層關系如圖5所示。圖6(a)顯示了各地層界面與剖切面的交線和交點情況，圖6(b)是附加地層屬性信息后得到剖曲面處的地層信息，需要說明的是在圖6(b)中只顯示剖切面與地層公共部分，對多余剖面部分沒有顯示，這樣容易定位地層。

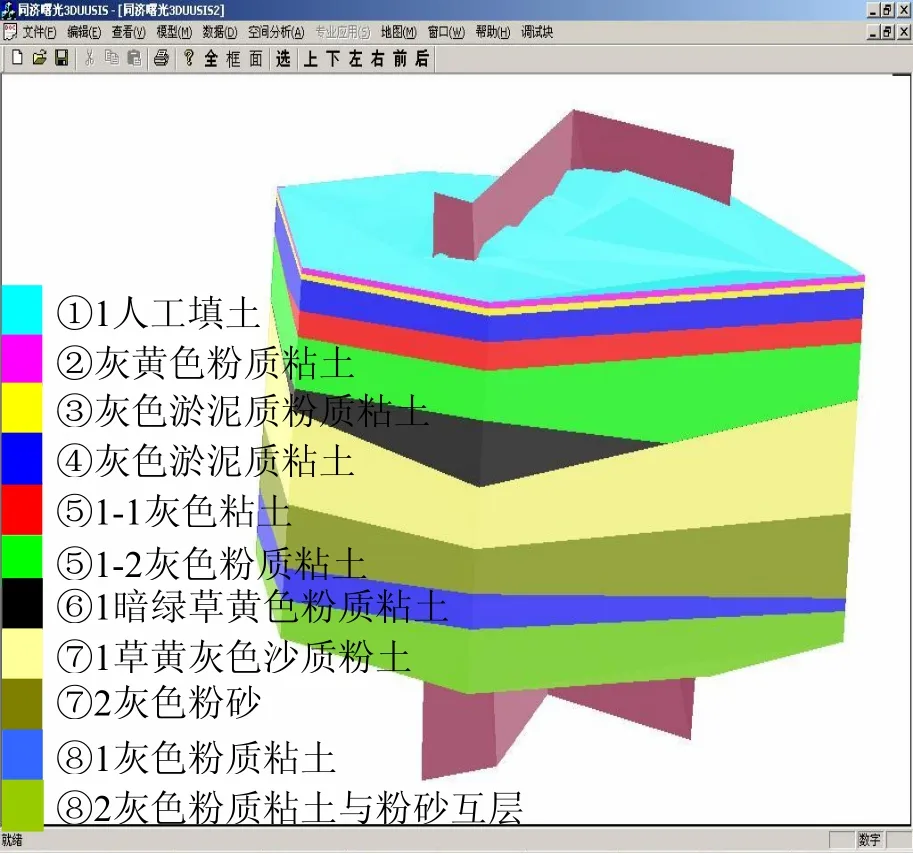
圖5 地層與剖曲面的關系

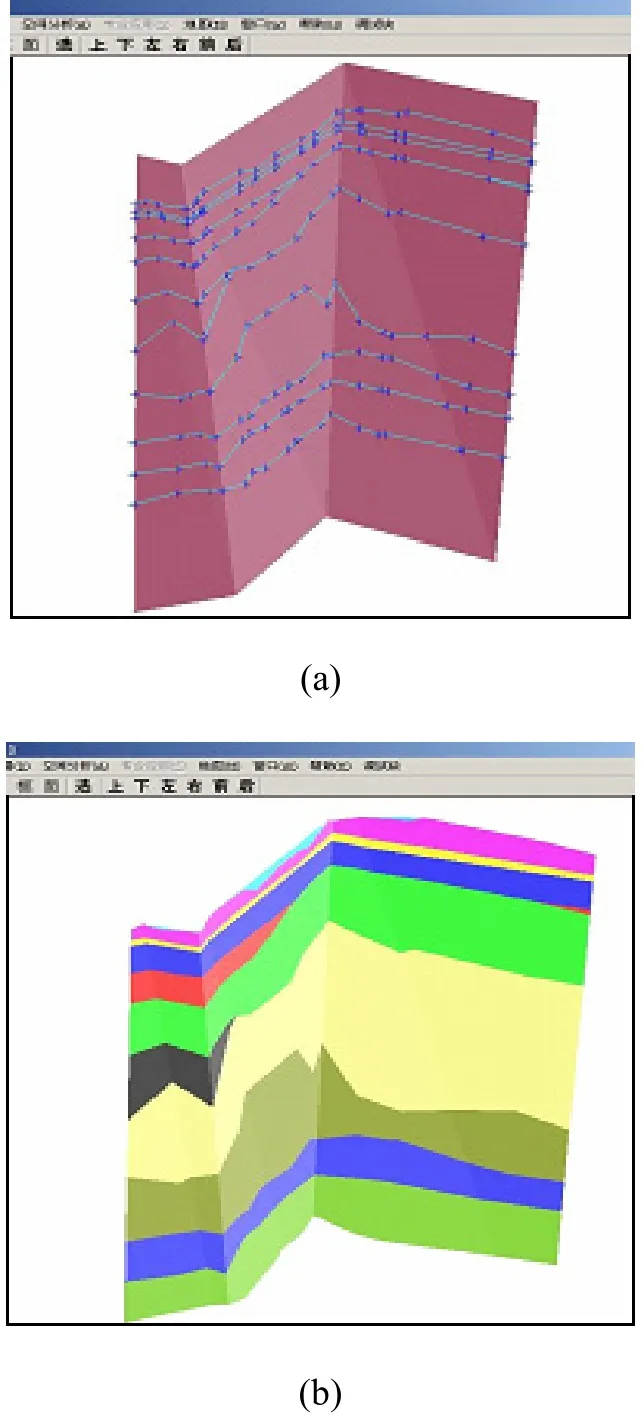
圖6 剖切曲面處地層信息

2.2 地下連續墻建模與分析

地下連續墻作為圍護結構以及地下結構的部分外墻，其本身的強度與穩定直接關系到整個基坑工程的成敗。本文利用巖土工程勘測報告（2005）提供的地下連續墻槽段平面布置圖（圖7(a)）提取出槽段信息（圖 7(b)）作為地下連續墻建模的數據源，生成地下連續墻模型（圖8）。這點實現了從CAD圖到三維表達的自動生成，與設計單位習慣相符合。

施工中地下連續墻每個槽段處的地層信息很關健，本文利用生成的地下連續墻模型與三維地層模型（圖9）相疊加，得到每個槽段處的地層信息（圖10）。

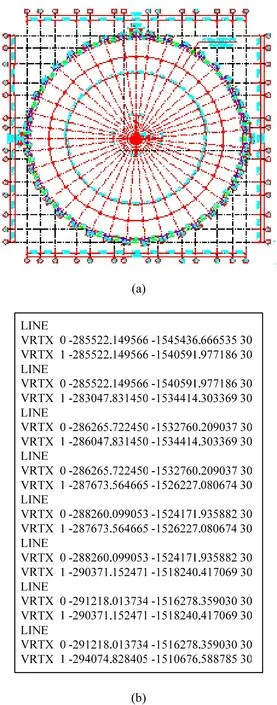
圖7 地下連續墻槽段平面布置圖(巖土工程勘測報告2005)及提取出來的槽段信息

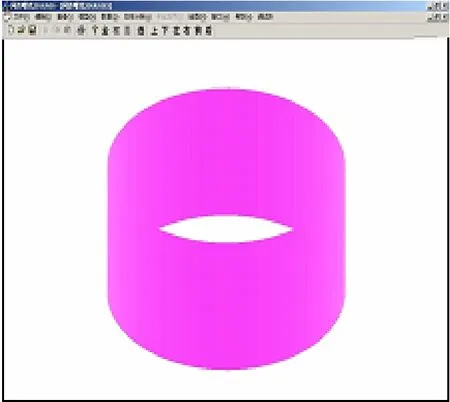
圖8 地下連續墻模型

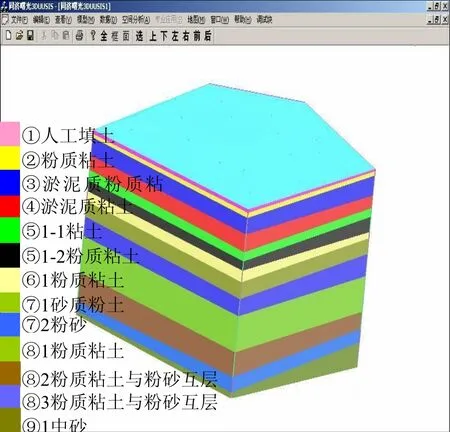
圖9 三維地層表面模型

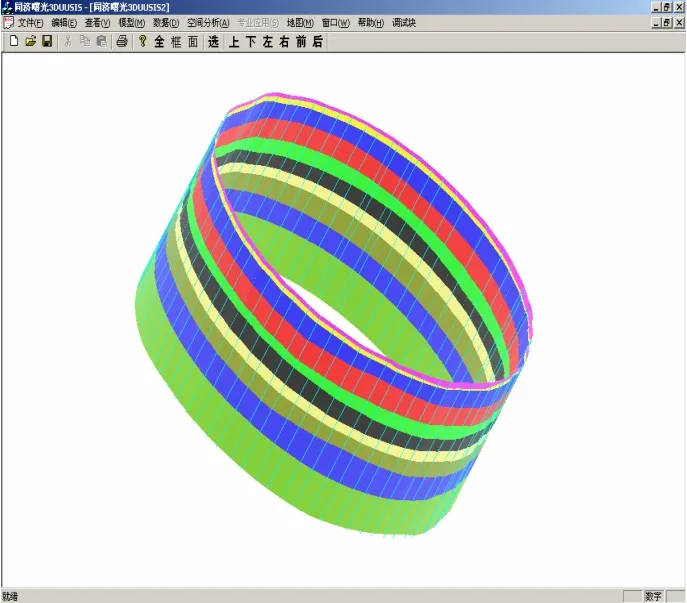
圖10 按槽段顯示地下連續墻的地層信息

3 結 束 語

三維TIN與TIN相交算法是幾何造型、計算機輔助設計、GIS空間分析和三維地質建模系統中的基礎算法，本文根據已知地層鉆孔離散數據的特點，綜合兩個方法的優點，編制實現了三維TIN與TIN相交算法。并采用面向對象思想，對幾何基元及相關算法類的數據結構進行了設計，該算法既能靈活的設定曲面形狀與方向，又能夠顧及到復雜的約束條件。經過實際工程應用，驗證了方法正確性和應用價值。

[1]Martin Held, ERIT. A collection of efficient and reliable intersection tests [R]. Technical Report,University at Stony Brook, 1996.

[2]Tomas M?ller. A fast triangle-triangle intersection test [J].Journal of Graphics Tools, 1997, 2(2)：25-30.

[3]Olivier Devillers, Philippe Guigue. Faste triangle-tri angle intersection tests [R]. INRIA, 2002.

[4]張 芳. 場框架下的城市地下空間三維數據模型及相關算法研究[D]. 上海：同濟大學, 2006.

3D TIN Intersection Algorithm and Its Application in Geotechnical Engineering

ZHANG Fang1, ZHU He-hua2

( 1. BGI Engineering Consultants LTD, Beijing 100038, China; 2.Department of Geotechnical Engineering, Key Laboratory of Geotechnical and Underground Engineering (Tongji University), Ministry of Education, Shanghai 200092, China )

The geology cross-section is one of the normal means to describe geological structure. In this paper, an intersection algorithm between 3D TIN and TIN is accomplished to cut arbitrary cross section from the 3D geology model. The principle of the algorithm, the design of data structure and the calculation process are described in details. The algorithm can arbitrarily set the boundary shape and direction of cross-section and regard the complicated stipulation condition as well. Finally, the validity and the application value of the algorithm is testified by its application in two projects.

computer application; 3D TIN’s intersection algorithm; section; spatial analysis

P 208

A

1003-0158(2010)05-0151-06

2008-12-20

張 芳（1976-），女，遼寧大連人，工程師，博士，主要研究方向為巖土及地下工程數字化、水文地質與工程地質。